МУ к выполнению курсовой работы. Методические указания Саратов введение цель работы практическое освоение методов проектирования сварных конструкций (СК)
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Как отмечено в разделе 3, низкие значения φ свидетельствуют о нерациональном использовании металла. В связи с этим гибкость ограничивают. Для сжатых стоек она должна быть не выше 120. После определения φ устойчивость стойки проверяют по формуле Если стойка сжата внецентренно, то изгиб ослабляет устойчивость и значение φ снижается. Рассмотрим вначале изгиб только относительно оси x (при My=0) (см. рис. 1). Рационально подобранное сечение имеет наименьшую гибкость в плоскости действия момента. В связи с этим под действием изгибающего момента потеря устойчивости может произойти как в плоскости наименьшей гибкости, в которой действует момент Mx, так и в плоскости наибольшей гибкости. В любом случае устойчивость снижается с увеличением гибкости и относительного эксцентриситета mx (см. формулу 1). Рассмотрим вначале потерю устойчивости в направлении наибольшей гибкости, перпендикулярном плоскости действия момента Mx. При этой изгибно-крутильной форме потери устойчивости происходит закручивание стойки, и плоскость с наибольшей гибкостью поворачивается в направлении плоскости действия момента Mx. Расчет устойчивости проводят по формуле (20), вычисляя коэффициент φ по формуле φ=φy·c. Коэффициент φy определяют так же, как при центральном сжатии, по табл. 6, в зависимости от гибкости стойки λy (λy0) при изгибе вокруг оси y. Коэффициент c учитывает дополнительное снижение устойчивости от действия момента Mx. Коэффициент α для типов сечений, предложенных в задании, равен 0,6 при mx≤1 и (0,55+0,05·mx) при 1 < mx≤5; коэффициент β равен 1 при гибкости λy< 100. Для других сечений и для λy >100 следует определять α и β по табл. 10 СНиП. Влияние изгиба в плоскости действия момента Mx не удается свести к одному поправочному коэффициенту. Расчет проводят по формуле (20), а коэффициент φ=φmx определяют по более сложным таблицам, учитывающим одновременное влияние гибкости λx (λx0) в плоскости действия момента и относительного эксцентриситета mx. Для ВСтЗсп и типов сечений, указанных в задании, значения φmx можно найти по табл. 7, если x - материальная ось сечения, и по табл. 8, если x - свободная ось. Для других материалов, типов и соотношений размеров сечений следует определять φmx по табл. 74 и 75 приложения 6 СНиП. Таблица 7
Табл.8
В случае изгиба в двух направлениях, когда в плоскости наибольшей жесткости действует момент Mx, а в другой плоскости My, вначале проводят проверку устойчивости в плоскости действия момента Mx без учета My, (с коэффициентом φ=φmx), а затем дополнительную проверку по той же формуле (20), но подставляя коэффициент Значения φmyопределяют в зависимости от гибкости λy (λy0) и относительного эксцентриситета my по табл. 7, если ось y материальная или по табл. 8, если ось y свободная. Коэффициент c находят по формуле (21). Таким образом, коэффициент φmxy учитывает влияние сразу двух изгибающих моментов - Mx и My. 7. Проверочный расчет общей устойчивости балки В балке, так же как и в стойке, происходит изгибно-крутильная потеря устойчивости, если моменты инерции ее сечения относительно двух поперечных осей x и y сильно отличаются. Сечения в средней части балки поворачиваются таким образом, что под действием момента Mx, происходит изгиб не вокруг оси x, а вокруг оси y. Такое явление наблюдается в балках двутаврового и швеллерного сечений. В балках коробчатого сечения (см .рис.3) потеря устойчивости, как правило, не происходит, так как моменты инерции их сечений относительно осей x и y близки по значению. Устойчивость может быть обеспечена либо за счет увеличения момента инерции балки Iy, либо за счет горизонтальных связей, прикрепляющих балку к опоре. В балке, состоящей из двух ветвей, может происходить потеря устойчивости одной ветви. В этом случае устойчивость обеспечивают горизонтальные связи, скрепляющие ветви балки. Расчет на устойчивость проводят по формуле Процедура определения φи состоит из нескольких этапов. Вначале определяют коэффициент α. Для сварного двутавра или швеллера 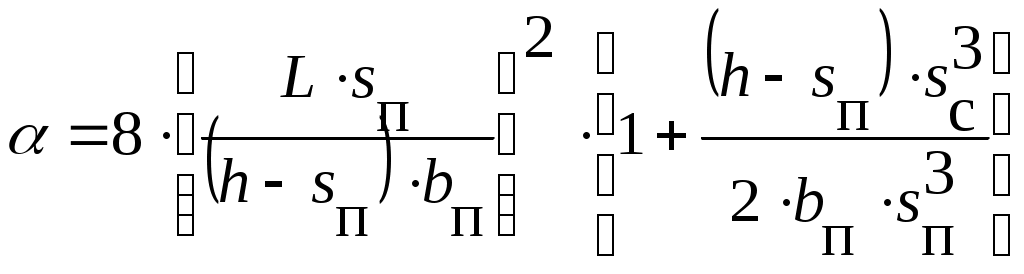 где L - длина балки (расстояние между осями связей, если имеются горизонтальные связи); h - высота балки; sc - толщина стенки; sп, bп - толщина и ширина полки. Для прокатного двутавра или швеллера где Iкр- момент инерции балки при кручении, Iy - момент инерции при изгибе в плоскости, перпендикулярной плоскости действия момента Mx. Далее по табл. 77 и 78 Приложения 7 СНиП определяют другой коэффициент - ψ. В случае консольно закрепленной балки двутаврового сечения с нагрузкой, приложенной на конце балки к нижнему поясу ψ=6,2+0,008·α при α≤28; ψ=7,0+0,005·α при α>28. При проверке устойчивости ветви балки составного сечения, подкрепленной горизонтальными связями с другими ветвями ψ=2,25+0,07·α при α≤40;ψ=3,6+0,04·α7a 0 -3,5·105·α2 при α> 40. Следующий коэффициент - φ1 рассчитывают по формуле: где Ix - момент инерции при изгибе в плоскости действия момента Mx; E, Ry - модуль упругости и расчетное сопротивление металла. Если профиль - швеллер, а не двутавр, то полученное значение φ1 следует умножить на 0,7. Искомый коэффициент φи равен φ1,если φ1≤0,85. Если φ1> 0,85 , то вводят поправку: φи=0,68+0,21φ1. Если при этом φи≥1, то общая устойчивость обеспечена, если же φи<1, то проводят проверку устойчивости по формуле (22). Формула (23) показывает, какие действия можно предпринять по повышению устойчивости, если не выполнено условие (22). Для балки без горизонтальных связей единственным способом является увеличение жесткости в поперечном направлении Iy за счет увеличения толщины или ширины полок. Устойчивость ветвей составного сечения может быть повышена за счет добавления связей между ветвями. При этом уменьшается свободная длина ветви L в формуле (23), и значение φи повышается. Нет необходимости очень сильно повышать φ1, так как уже при φ1≥1,52 устойчивость полностью обеспечена. 8. Проверочный расчет местной устойчивости элементов сечения Эта проверка необходима, если в сечении имеются широкие и тонкие листовые элементы. Чаще всего теряют устойчивость стенки балок. Для обеспечения устойчивости стенки при отсутствии сжимающих стенку сосредоточенных сил необходимо выполнить условие: Устойчивость полок сварной двутавровой балки обеспечена, если При одинаковом соотношении ширины и толщины стенка балки имеет большую устойчивость, согласно формулам (27) и (28), чем половинка полки, так как обе кромки стенки являются жесткими за счет прикрепления к полкам, а край полки ничем не подкреплен и может свободно изгибаться. Формулы (27) и (28) пригодны и для проверки устойчивости полок и стенок сечения стойки. При проверке устойчивости полок прокатанных и гнутых элементов в формулу (28) вместо bп/2 подставляют значение расстояния от начала внутреннего закругления до края полки двутавра, швеллера или уголка. Если местная устойчивость полки профиля по (28) не обеспечена, необходимо изменить соотношение ширины и толщины полки.Устойчивость стенки балки можно обеспечить приваркой поперечных и продольных ребер жесткости. Приварка ребер необходима, если не выполнено условие (27). Устойчивость стенки, подкрепленной поперечными ребрами, при отсутствии сосредоточенных сжимающих сил, обеспечена, если выполняется условие где | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
