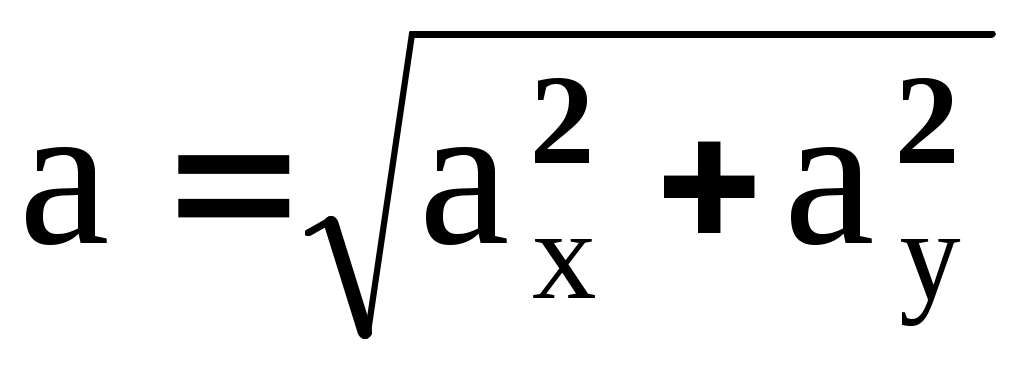Статика-кинематика. Статика-кинемат. Методические указания входят задания по первой части курса (статика и кинематика)
 Скачать 5.91 Mb. Скачать 5.91 Mb.
|
|
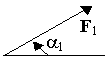
МЕТОДИЧЕСКИЕ УКАЗАНИЯ В курсе теоретической механики студенты изучают разделы статика кинематика и динамика. В настоящие методические указания входят задания по первой части курса (статика и кинематика). Дается перечень вопросов, которые как основная часть курса, должны изучаться студентами всех специальностей. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА РАБОЧАЯ ПРОГРАММА Введение. Механическое движение как одна из форм движения материи. Предмет механики. Теоретическая механика и ее место среди естественных и технических наук. Механика как теоретическая база ряда областей современной техники. СТАТИКА ТВЕРДОГО ТЕЛА Основные понятия и аксиомы статики. Предмет статики. Основные понятия статики: абсолютно твердое тело, сила, эквивалентные и уравновешенные системы сил, равнодействующая, силы внешние и внутренние. Аксиомы статики. Связи и реакции связей. Основные виды связей: гладкая плоскость или поверхность, гладкая опора, гибкая нить, цилиндрический и сферический шарниры, невесомый стержень реакции этих связей. Система сходящихся сил. Геометрический и аналитический способы сложения сил. Сходящиеся силы. Равнодействующая сходящихся сил. Геометрическое и аналитическое условия равновесия системы сходящихся сил. Система сил, расположенных на плоскости (плоская система сил). Алгебраическая величина момента силы. Пара сил, ее свойства. Теорема о параллельном переносе силы. Аналитические условия равновесия плоской системы сил. Условия равновесия плоской системы параллельных сил. Теорема Вариньона о моменте равнодействующей. Распределенная нагрузка. Расчет составных конструкций. Расчет ферм. Произвольная пространственная система сил. Момент силы относительно оси. Приведение пространственной системы сил к простейшему виду. Условия равновесия произвольной пространственной системы сил. Сцепление и трение тел. Законы Амонтона-Кулона. Коэффициенты сцепления и трения скольжения. Угол и конус трения. Трение качения. Центр тяжести. Центр тяжести твердого тела и его координаты. Центр тяжести объема, площади и линии. Способы определения положения центров тяжести. КИНЕМАТИКА Введение в кинематику. Предмет кинематики. Пространство и время в классической механике. Относительность механического движения. Система отсчета. Задачи кинематики. Кинематика точки. Векторный способ задания движения точки. Траектория точки. Скорость точки как производная от ее радиус-вектора по времени. Координатный способ задания движения точки в прямоугольных декартовых координатах. Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси. Естественный способ задания движения точки. Оси естественного трехгранника. Алгебраическая величина скорости точки. Определение ускорения точки по его проекциям на оси естественного трехгранника: касательное и нормальное ускорения точки. Кинематика твердого тела. Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении. Вращение твердого тела вокруг неподвижной оси. Уравнение (закон) вращательного движения твердого тела. Угловая скорость и угловое ускорение тела. Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси. Плоскопараллельное движение твердого тела. Уравнения движения. Определение скоростей точек плоской фигуры. Сложное движение точки. Относительное, переносное и абсолютное движение. Теорема о сложении скоростей. Теорема Кориолиса. СПИСОК ЛИТЕРАТУРЫ Воронков И.М. Курс теоретической механики. М., 1954 и последующие издания. Гернет М.М. Курс теоретической механики. М., 1970 и последующие издания. Тарг С.М. Краткий курс теоретической механики. М., 1963 и последующие издания. Мещерский И.В. Сборник задач по теоретической механике. М., 1970 и последующие издания. Сборник задач по теоретической механике. / Под ред. К.С.Колесникова. М., 1983. Сборник задач для курсовых работ по теоретической механике / Под ред. А.А. Яблонского. М., 1972 и последующие издания. (Содержит примеры решения задач.) Пирогов С.П. Краткий курс лекций по теоретической механике. Тюмень, «Вектор Бук», 2001 г. КОНТРОЛЬНОЕ ЗАДАНИЕ СОДЕРЖАНИЕ ЗАДАНИЙ, ВЫБОР ВАРИАНТОВ, ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ, ОБЩИЕ ПОЯСНЕНИЯ К ТЕКСТУ ЗАДАЧ Контрольное задание состоит из четырех задач - С1, С2,К1, К2. К каждой задаче (кроме К1) дается 10 рисунков и таблица (с тем же номером, что и задача), содержащая дополнительные к тексту задачи условия. Нумерация рисунков двойная, при этом номером рисунка является цифра, стоящая после точки. Например, рис. С1.4- это рис. 4 к задаче С1 и т.д. (в тексте задачи при повторных ссылках на рисунок пишется просто рис. 4). Номера условий от 0 до 9 проставлены в 1-м столбце (или в 1-й строке) таблицы. Студент во всех задачах выбирает номер рисунка по предпоследней цифре шифра, а номер условия в таблице - по последней; например, если шифр оканчивается числом 46, то берет рис. 4 и условия № 6 из таблицы. Задание выполняется в отдельной тетради (ученической), страницы которой нумеруются. На обложке указываются : название дисциплины, номер работы, фамилия и инициалы студента, учебный шифр, факультет, специальность и адрес. На первой странице тетради записываются: номер работы, номера решаемых задач и год издания контрольных заданий. Методические указания по решению задач, входящих в контрольные задания, даются для каждой задачи после изложения ее текста под рубрикой “Указания”; затем дается пример решения аналогичной задачи. Цель примера - разъяснить ход решения, но не воспроизвести его полностью. Поэтому в ряде случаев промежуточные расчеты опускаются. Но при выполнении задания все преобразования и числовые расчеты должны быть обязательно последовательно проделаны с необходимыми пояснениями; в конце должны быть даны ответы. ЗАДАЧИ К КОНТРОЛЬНЫМ ЗАДАНИЯМ СТАТИКА Задача С1 Жесткая рама (рис. С1.0 - С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена к шарнирной опоре на катках. На раму действуют пара сил с моментом М=100 Нм и сила, значение, направление и точка приложения которой указаны в таблице (например, в условиях № 1 на раму действует сила F1 = 10 Н под углом 30 к горизонтальной оси, приложенная в точке К). Определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять L=0,5 м. Указания. Задача С1 - на равновесие тела под действием плоской системы сил. Составляя уравнения равновесия, учесть, что уравнение моментов будет более простым (содержать меньше неизвестных),    Таблица С1
если брать моменты относительно точки, где пересекаются линии действия двух реакций связей (в данном случае относительно точки B). При вычислении момента силы F часто удобно разложить ее на составляющие F/ и F//, для которых плечи легко вычисляются, в частности на составляющие, параллельные координатным осям, и воспользоваться теоремой Вариньона; тогда mO(F)=m0(F/)+m0(F//). Пример С1. Жесткая рама АВС ( рис. С1 ) имеет в точке B неподвижную шарнирную опору, а в точке C - подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке. 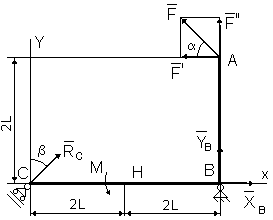 Рис. С1 Дано: F=25 кH, =60o, =30, М=50 кHм, L=0,5 м. Определить: реакции в точках B и C, вызываемые действующими нагрузками. Решение. Рассмотрим равновесие рамы. Проведем координатные оси ХУ и изобразим действующие на раму силы: силу F, пару сил с моментом М и реакции связей XB, YB, RC (реакцию неподвижной шарнирной опоры B изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости). Составим три уравнения равновесия плоской системы сил. При вычислении момента силы F относительно точки B воспользуемся теоремой Вариньона, т.е. разложим силу F на составляющие F’, F’’ (F’=Fcos , F’’=Fsin ) и учтем, что mB(F)=mB(F’ )+mB(F'' ). Получим : 1. Fkx = 0, XB + RC sin - F cos = 0; 2. Fky = 0, УB + RC cos + F sin = 0; 3. mB(Fk) = 0, M - RCcos4L+ F cos 2L= 0. Из этих уравнений находим: Из (3): Из (1): XB = - RC sin + F cos; Из (2): YB = - RC cos - F sin; Подставив в составленные уравнения числовые значения заданных величин, и решив эти уравнения, определим искомые реакции. Ответ: XB = - 5,5 кH, YB = 9,6 кH, RC =36,1 кH. Знаки указывают, что сила XB направлена противоположно показанной на рис.С1. Задача С2 Рама, состоящая из двух абсолютно твердых ломаных стержней, соединенных между собой шарниром, (рис. С2.0 – С2.9, табл. С2) закреплена в точке А жесткой заделкой, а в точке В прикреплена к шарнирной опоре на катках. Положение шарнира указано в табл.С2. На раму действуют: пара сил с моментом М=100 Нм и сила, значение, направление и точка приложения которой указаны в таблице (например, в условиях № 1 на раму действует сила F1 = 10 Н под углом 30 к горизонтальной оси, приложенная в точке D), а также распределенная нагрузка интенсивностью q=20 Н/м, приложенная на участке, указанном в таблице. Если распределенная нагрузка приложена на горизонтальном участке, то она действует вниз, а если на вертикальном, то вправо. Определить реакции связей в точках А и В, вызываемые заданными нагрузками, а также реакцию внутренней связи. При окончательных подсчетах принять L=0,5 м. Указания. Задача С2 - на равновесие составных конструкций под действием плоской системы сил. Для определения всех силовых факторов в заделке и реакций шарнирной опоры и внутренней связи необходимо рассмотреть равновесие каждого тела, из которых состоит рама, отдельно, учитывая, что силы взаимодействия между телами равны по величине и противоположны по направлению.    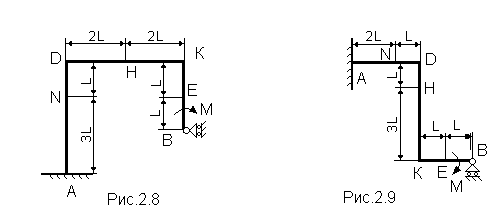 Таблица С2
Пример С2. Рама, состоящая из двух изогнутых стержней, соединенных между собой шарниром С, закреплена в точке А жесткой заделкой, а в точке В прикреплена к шарнирной опоре на катках. Определить реакции связей в точках А и В, вызываемые заданными нагрузками, а также реакцию внутреннего шарнира С (рис.С2,а). Дано: F=20H, M=50 HM, q=10H/м. Решение. Рассмотрим равновесие отдельных участков рамы, разделив ее в шарнире С. При этом к левому участку рамы (рис.С2,в) согласно аксиоме отбрасывания связей будут приложены силы реакции опоры В – Rв и реакция в шарнире С, которую разложим на две составляющие – Хс и Ус, а на правую (рис.С2,б) – реакции заделки: силы Ха и Уа, реактивный момент Ма, реакции шарнира С :  Составим уравнения равновесия плоской системы сил, приложенной к правой части рамы (рис.С2,в). Составим уравнения равновесия плоской системы сил, приложенной к правой части рамы (рис.С2,в).1. 2. 3. Из (1): из (3): из (2): Затем составим уравнения равновесия плоской системы сил, приложенной к правой части рамы (рис.С2,б). При этом распределенную нагрузку заменяем равнодействующей Q=3q=30 H, приложенной в центре участка приложения нагрузки. 4. 5. 6. Из этих уравнений находим: Из (4): Из (5): Из (6): КИНЕМАТИКА Задача К1 Точка В движется в плоскости xy (табл. К1.1, К1.2). Закон движения точки задан уравнениями: x=f1( t ), y=f2( t ), где x и y выражены в сантиметрах, t - в секундах. Найти уравнение траектории точки; для момента времени t1=1c определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Зависимость x=f1( t ) указана в табл. К1.1, а зависимость y=f2(t) дана в табл. К1.2 (для вар.0 - 2 в столбце 2, для вар.3 - 6 в столбце 3, для вар.7 - 9 в столбце 4). Номер варианта в табл. К1.1 выбирается по предпоследней цифре шифра, а номер условия в табл. К1.2 - по последней. Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах ( координатный способ задания движения точки ), а также формул, по которым определяются касательное и нормальное ускорения точки. В данной задаче все искомые величины нужно определить только для момента времени t1=1с. Таблица К1.1
Таблица К1.2
Пример К1. Даны уравнения движения точки в плоскости ху : x = 2 t , y = t2 (1) (х, у - в сантиметрах, t - в секундах). Определить уравнение траектории точки; для момента времени t1 = 1 c найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Решение. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Отсюда находим следующее уравнение траектории точки (парабола, рис. К1): y = x2 / 4 (2) Скорость точки найдем по ее проекциям на координатные оси: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Номер | Дано | Найти | |
| условия | | скорости | ускорения |
| 0 | s4 = 4(7t - t2) | vA, vB | 1, aA, a3 |
| 1 | v4 = 2(t2 - 3) | vA, vB | 2, aB, a3 |
| 2 | 1 = 2t2 - 9 | v3, 1 | 2, aB, a4 |
| 3 | 2 = 7t - 3t2 | v4, 1 | 2, aB, a4 |
| 4 | 2 = 3t - t2 | v3, 2 | 2, aA, a4 |
| 5 | 1 = 5t - 2t2 | v4, vA | 2, aB, a3 |
| 6 | 1 = 2(t2 - 3t) | v3, 2 | 2, aB, a4 |
| 7 | V3 = 3t2 - 8 | vB, 1 | 1, aA, a4 |
| 8 | s4 = 2t2 - 5t | v3, 1 | 1, aB, a3 |
| 9 | 1 = 8t - 3t2 | v4, vA | 1, aB, a3 |
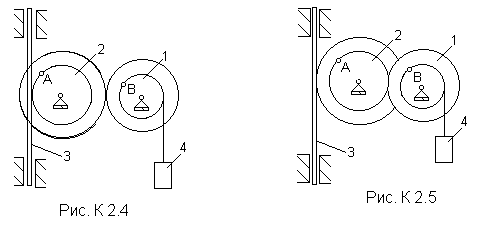
твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны ременной передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы; при этом считается, что ремень по ободу колеса не скользит.
Пример К2. Рейка 1, ступенчатое колесо 2 с радиусами R2 и r2 и колесо 3 радиуса R3, скрепленное с валом радиуса r3, находятся в зацеплении; на вал намотана нить с грузом 4 на конце ( рис. К2). Рейка движется по закону s1=f( t ).
Дано: R2=6 см, r2=4 см, R3=8 см, r3=3 см, s1=3t3 (s - в сантиметрах, t - в секундах), А - точка обода колеса 3, t1=3 c.
Определить: 3, v4, 3, aA , в момент времени t=t1.

Рис.К2
Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса Ri), через vi, а точек, лежащих на внутренних ободах (радиуса ri), - через ui.
Определяем сначала угловые скорости всех колес как функции времени t. Зная закон движения рейки 1, находим ее скорость:
v1 =
Так как рейка и колесо 2 находятся в зацеплении, то v2=v1 или w2R2=v1. Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, u2=v3 или w2r2=w3R3. Из этих равенств находим
Тогда для момента времени t1=3 c получим w3=6,75 c-1.
Определяем v4. Так как v4=vB=3r3, то при t1=3 c v4=20,25 см/c.
Определяем 3. Учитывая второе из равенств (2), получим
3=
Определяем aA. Для точки А
a= 36 см/c2, anA = 364 см/c2;
Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис.К2.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное
образовательное учреждение высшего образования
«тюменский индустриальный университет»
институт транспорта
Кафедра «Прикладная механика»
«Сопротивление материалов»
Методические указания для студентов заочной формы обучения (раздел 1)
Составители:
Б.А. Гуляев, кандидат технических наук, доцент;
Ю.Е. Якубовский, доктор технических наук, профессор
Тюмень
ТИУ
2016