атомная физика на английском. Методическое пособие по лабораторному практикуму Атомная физика часть 1 для студентов 3 5 курсов физического факультета
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
1. КРАТКАЯ ТЕОРИЯ2. ОПИСАНИЕ УСТАНОВКИ3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ4. КОНТРОЛЬНЫЕ ВОПРОСЫ ЦЕЛЬ РАБОТЫ Изучение сериальных закономерностей в спектрах водорода и дейтерия; экспериментальное определение длин волн серии Бальмера двух изотопов водорода, определение спектроскопическим методом постоянной Ридберга, потенциала ионизации. 1. КРАТКАЯ ТЕОРИЯИзлучение возбужденных атомов и атомных систем можно характеризовать спектральным распределением (спектром): I=f(), I=f(), I=f(). Спектр изолированных атомов является линейчатым, т.е. состоит из отдельных, резко обозначенных линий. Атомы каждого химического элемента имеют свой определенный спектр излучения, не зависящий от способа возбуждения атома. Отдельные линии в спектрах могут быть объединены в группы линий – серии. Анализ экспериментального материала показал, что спектр излучения атома водорода можно представить состоящим из серий, частоты линий в которых подчиняются определенной закономерности: С R – определенная постоянная. n=3,4,5, … (1), С n=2,3,4, … (2) Серия Пашена (1908 г.) – n=4,5,6, … (3) Серия Брэккета – n=5,6,7, … (4) С n=6,7,8…(5) Каждую из частот можно представить разностью двух величин: ( г (7) называются спектральными термами. Первое теоретическое объяснение наблюдаемых закономерностей было дано в рамках теории Н. Бора. Основные положения теории Бора для атома водорода Постулаты Бора: Атомы могут длительное время находиться только в определенных стационарных состояниях. Энергии стационарных состояний E1, E2, E3, … образуют дискретный набор значений. При переходе атома из одного (начального) состояния в другое (конечное) стационарное состояние Em (Em (8) Исходя из представлений планетарной модели, вышеуказанные постулаты конкретизированы Бором в правилах квантования орбит: из множества круговых орбит стационарными являются лишь те орбиты, при движении по которым момент импульса электрона равен целому числу постоянных Планка: n=1,2,3, … (9) Целое число было названо квантовым числом. Правило квантования выделяет из всего множества орбит лишь дискретное множество, характеризуемое правилом (9). Позднее Вильсоном и Зоммерфельдом правила квантования (9) были обобщены на случай эллиптических орбит. При этом стационарная орбита определялась уже двумя квантовыми числами: n - азимутальное квантовое число, nr - радиальное квантовое число, которые связаны соотношением – n= n + nr - целое число, а число n было названо главным квантовым числом. Найдем стационарные круговые орбиты и соответствующие энергии. Будем считать ядро покоящимся, а электрон вращающимся по круговой орбите вокруг ядра. В этом случае центростремительная сила: 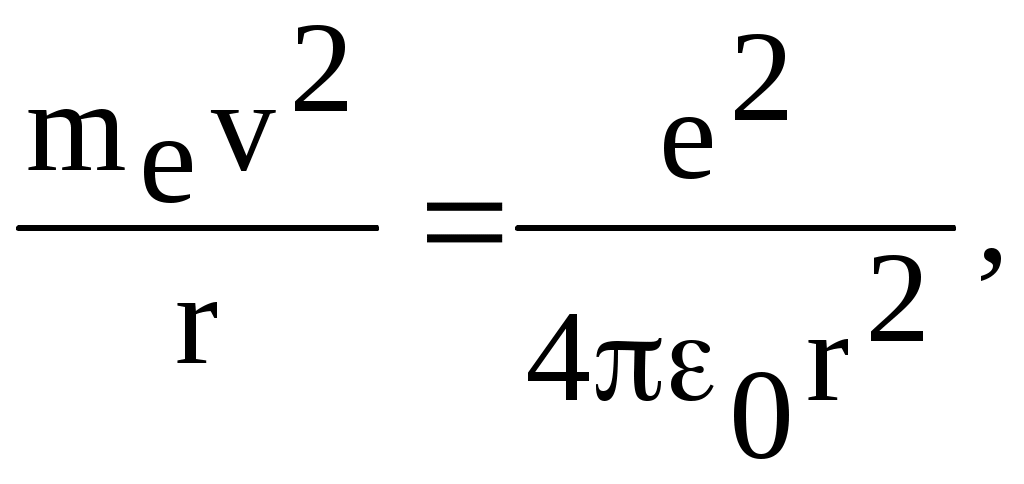 (10) г (11) П (12) Из (11), (12) для полной энергии электрона в атоме водорода получаем: ( Из правил квантования (9) следует: ( Выражая из (10) v2 и приравняв (14), получим выражение для радиусов стационарных круговых орбит электрона в атоме водорода: 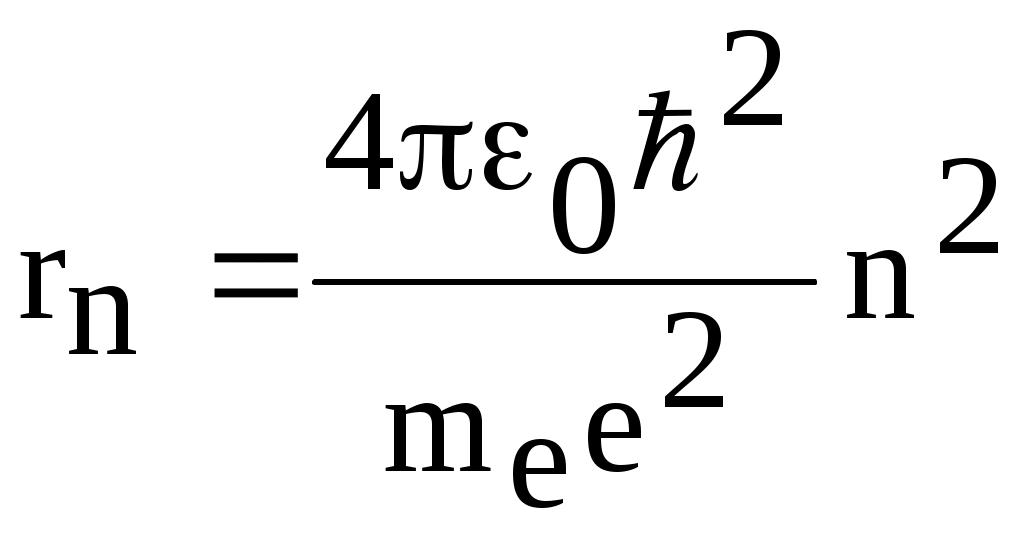 (15) Радиус первой орбиты (n=1), вычисленной по (15) и равный r1=a0=0,52910-10 м, получил название первый боровский радиус. Подставив (15) в (13), получим выражение, описывающее уровни энергии стационарных состояний электрона в атоме водорода: 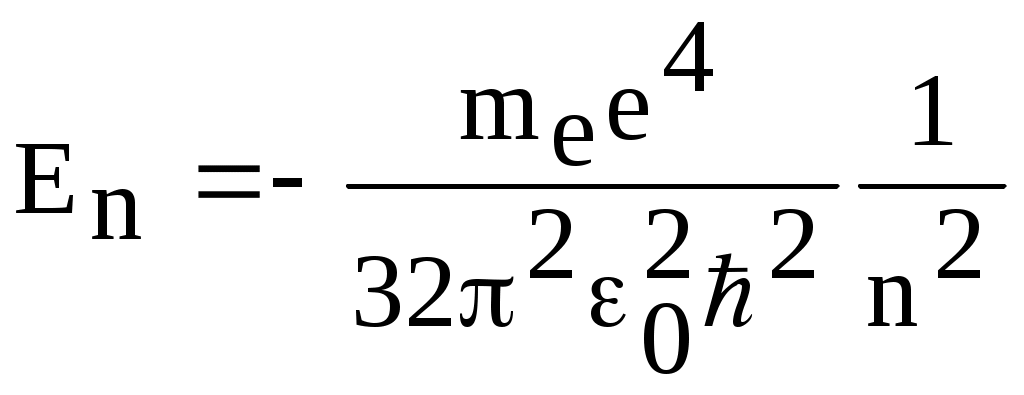 (16) Рассчитанная по (16) диаграмма энергетических уровней для атома водорода представлена на рис. 1. Стационарное состояние n=1, En=E1 названо основным состоянием, все остальные состояния (n>1) – возбужденные. При n, En0. Н 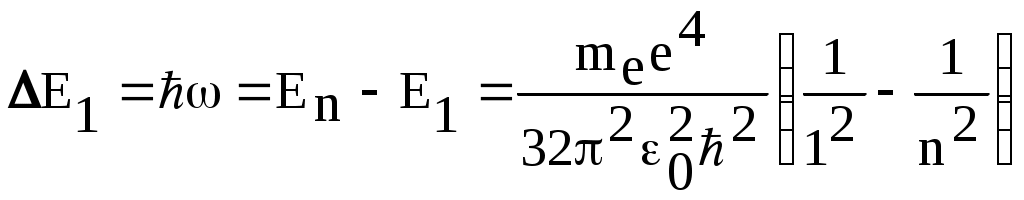 аблюдаемые сериальные закономерности в спектре атома водорода теперь получают простое объяснение. Исходя из постулатов Бора, атом излучает кванты электромагнитной энергии при переходах с выше лежащих энергетических уровней на ниже лежащие. Все возможные электронные электронные переходы, представленные на рис. 1 вертикальными стрелками, можно сгруппировать в серии. Для энергий квантов, соответствующих электронным переходам в основное состояние из всех вышележащих, можно записать: аблюдаемые сериальные закономерности в спектре атома водорода теперь получают простое объяснение. Исходя из постулатов Бора, атом излучает кванты электромагнитной энергии при переходах с выше лежащих энергетических уровней на ниже лежащие. Все возможные электронные электронные переходы, представленные на рис. 1 вертикальными стрелками, можно сгруппировать в серии. Для энергий квантов, соответствующих электронным переходам в основное состояние из всех вышележащих, можно записать:(17) n=2,3,4, … А 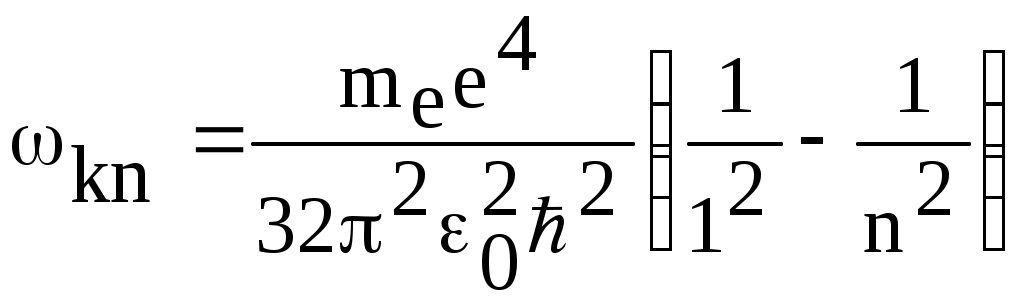 налогичное выражение можно записать для всех серий. Из рис. 1 и формулы (17) видно, что число спектральных линий в серии бесконечно. Таким образом, частоту,соответствующую какой-либо спектральной линии в каждой серии, можно представить общей формулой: налогичное выражение можно записать для всех серий. Из рис. 1 и формулы (17) видно, что число спектральных линий в серии бесконечно. Таким образом, частоту,соответствующую какой-либо спектральной линии в каждой серии, можно представить общей формулой:(18) где: k=1,2,3, … номер серии, n=k+1, k+2, … номер линии в серии. Г 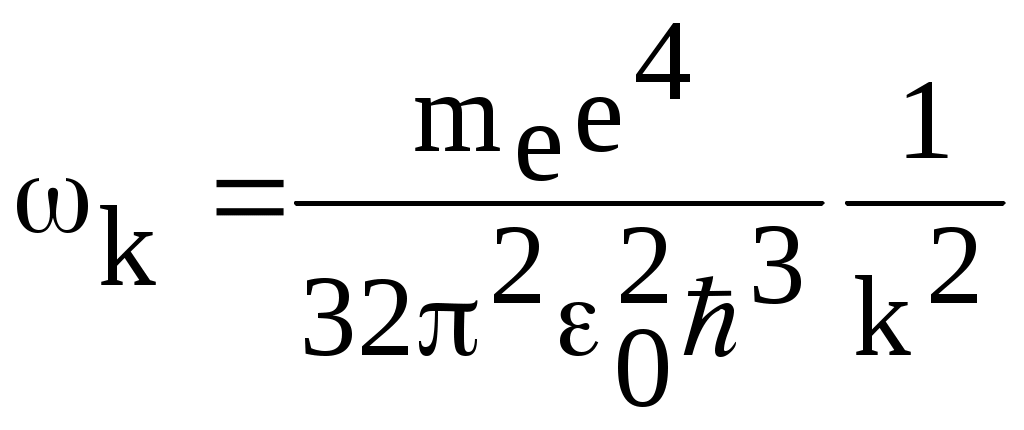 раница серии (n=) определяется: раница серии (n=) определяется:(19) О 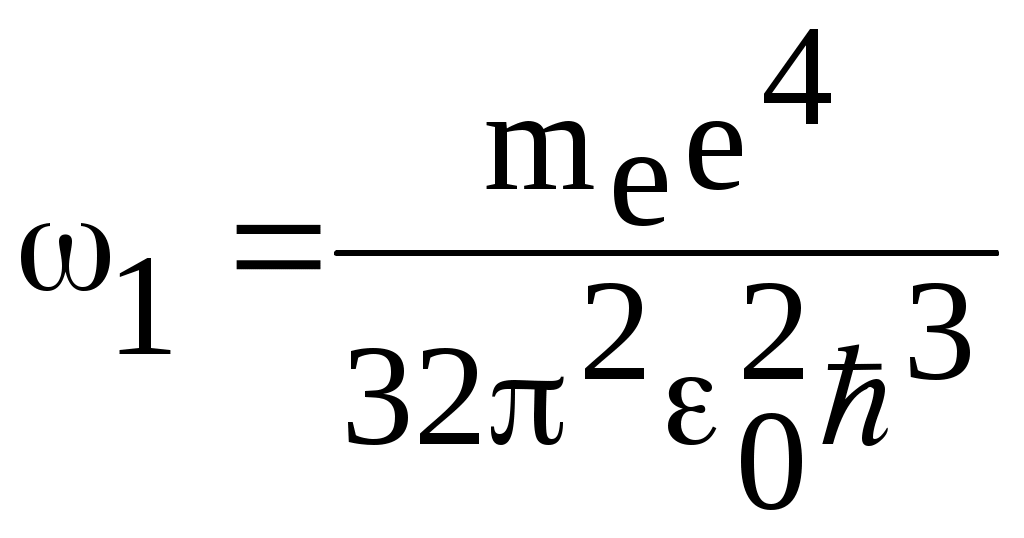 собый интерес представляет граница серии Лаймана (k=1): собый интерес представляет граница серии Лаймана (k=1):(20) З 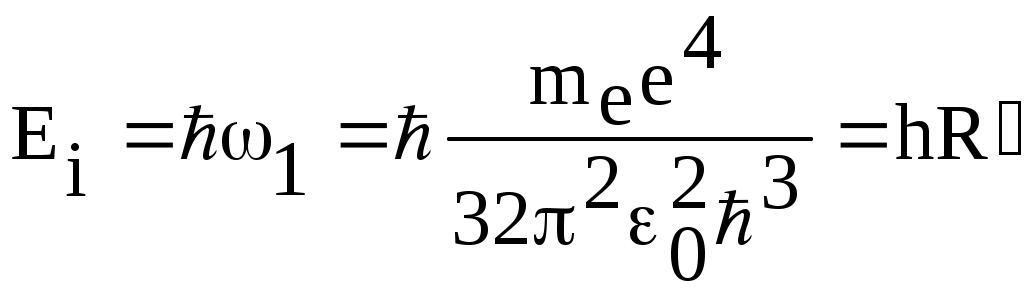 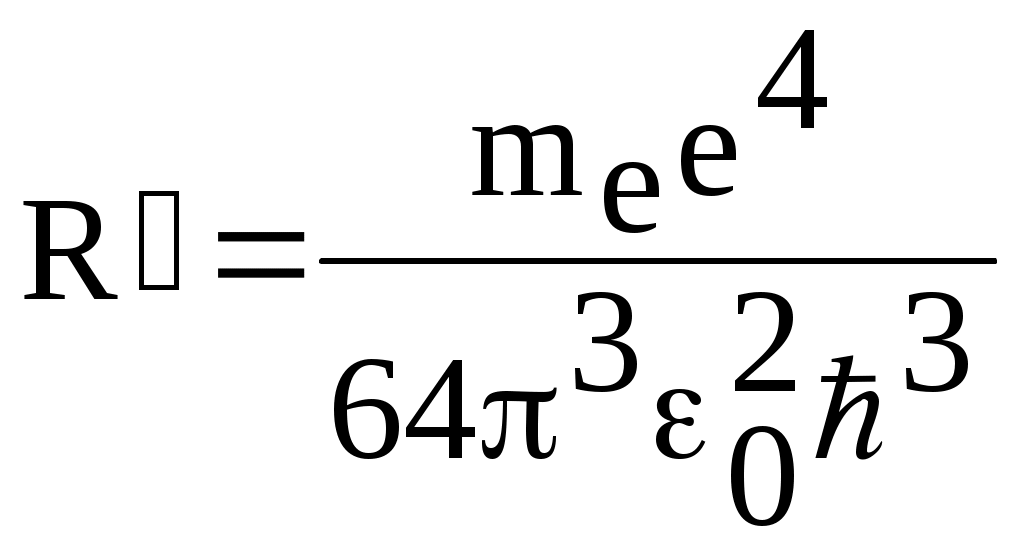 ная частоту граничной линии серии Лаймана, можно определить энергию, необходимую для отрыва электрона от атома водорода, находящегося в основном состоянии. Эта энергия называется энергией ионизации и определяется: ная частоту граничной линии серии Лаймана, можно определить энергию, необходимую для отрыва электрона от атома водорода, находящегося в основном состоянии. Эта энергия называется энергией ионизации и определяется:где: (21) - (22) Величину R можно сопоставить с введенной ранее постоянной R, которая названа постоянной Ридберга и рассчитана из спектров атома водорода (см. формулы 1 - 5) (R=3.2898421015 c-1 (Гц)), R=109677,581 см-1. Однако теоретическое значение R, рассчитанное по (22) и выраженное в соответствующих единицах, несколько отличаются: R=109737,303 см-1. Расхождение объясняется тем, что при выводе формулы (16) ядро считалось неподвижным и имеющим бесконечную массу. В действительности же, необходимо рассматривать движение обеих частиц вокруг центра масс. Тогда вместо массы электрона необходимо учитывать приведенную массу: (23) где: M – масса ядра (протона). С 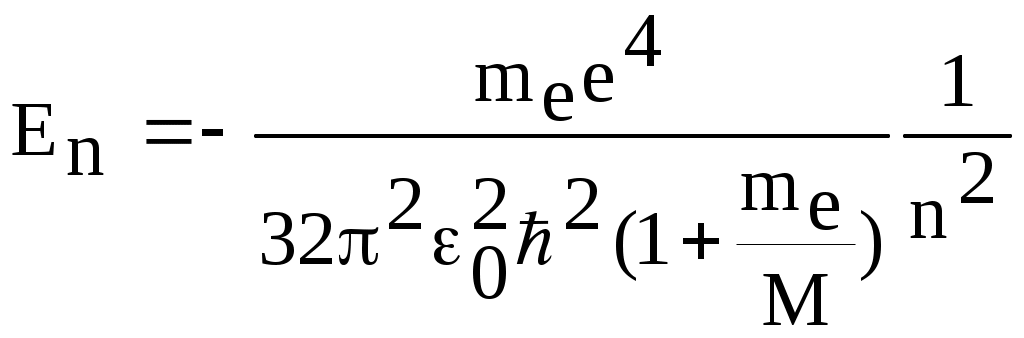 ледовательно, энергия стационарного состояния и пстоянная Ридберга должны зависеть от массы ядра: ледовательно, энергия стационарного состояния и пстоянная Ридберга должны зависеть от массы ядра: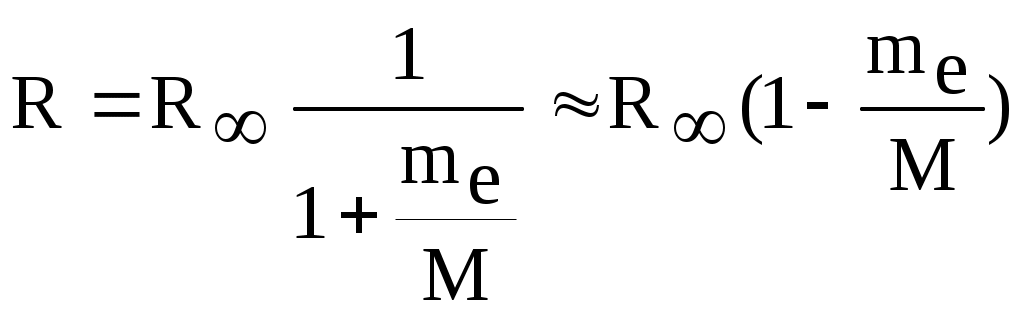 , (24)- (25) где: R - постоянная Ридберга, вычисленная в предположении бексконечно тяжелого ядра по формуле (22). Из формулы (23) следует, что приведенная масса будет иметь различные значения для разных изотопов и, следовательно, энергия системы “электрон-ядро” и спектральные термы формулы (7) будут иметь разные значения. В результате спектральные линии различных изотопов, обусловленные одним и тем же квантовым переходом nink, будут смещены друг относительно друга. Сдвиг терма относительно T: ( г 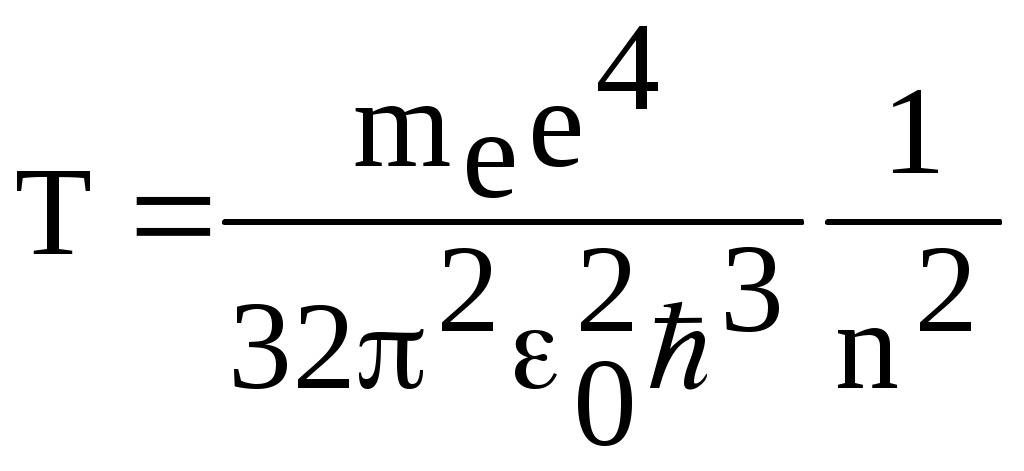 де: де: (27) Из (26,27) видно, что величина сдвига термов (энергетических уровней) убывает по мере возрастания n и на границе серии равна нулю. Терм более тяжелого изотопа имеет по модулю большую величину, т.е. соответствующий энергетический уровень тяжелого изотопа лежит “глубже” (отрицательное смещение термов). Для величины смещения между термами двух изотопов (M2>M1) можно получить: (28) Для частот этих двух изотопов (переход nink) получим: 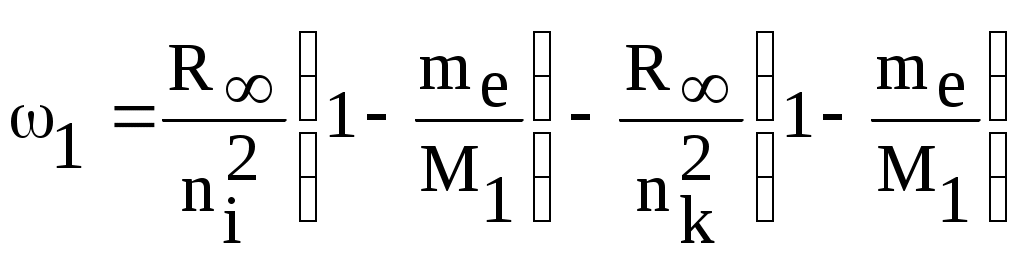 (29) 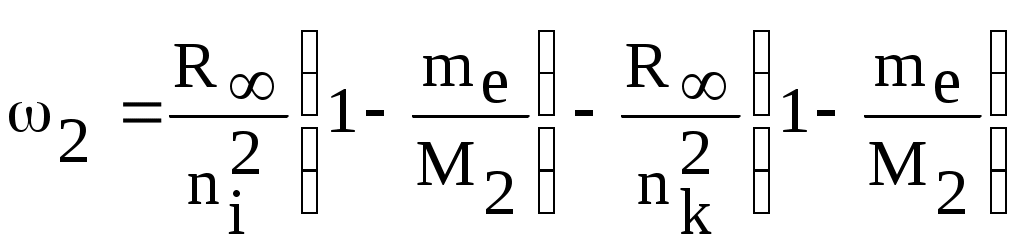 (30) Из (29,30) для величины изотопического смещения между линиями (nink) двух изотопов (M1, M2) получим: (31) Линия более тяжелое изотопа сдвинута в коротковолновую область спектра. Рассмотренный эффект называется нормальным изотопическим эффектом масс. Изотопический сдвиг хорошо виден для первых линий серии Бальмера атомов водорода и дейтерия. Четыре линии находятся в видимой области спектра и имеют следующее обозначение: красная линия - H и D (ni=3) сине-голубая линия - H и D (ni=4) голубая линия - H и D (ni=5) фиолетовая линия - H и D (ni=6). По экспериментально найденным значениям RH и RD можно вычислить массу электрона: (32) Более полное и точное решение задачи для атома водорода дает квантовая механика, где показано, что постановка задачи о траектории движения электрона в атоме лишена смысла. Можно лишь говорить о плотности вероятности местонахождения электрона. Вероятность того, что координаты электрона заключены между (r, r+dr), (,+d), (,+d) определяется: (33) где: r, , - координаты в сферической системе, dV - элемент объема, (r,,) волновая функция (собственная функция оператора Гамильтона). Волновая функция, являющаяся решением уравнения Шредингера для атома водорода, зависит от пространственных координат (r, , ), а также содержит три целочисленных параметра n, l, ml: (34) n - главное квантовое число, определяющее энергию атома, принимает ряд значений: n=1,2,3, …, Решение уравнения Шредингера для атома водорода дает выражение для полной энергии электрона (собственное значение оператора Гамильтона), совпадающее с формулой (16). l (36) Для каждого значения оно принимает ряд значений: l=0,1,2, … , (n-1), т.е. всего n значений. ml - магнитное орбитальное квантовое число, определяющее проекцию вектора Ll на ось z (физически выделенное направление в пространстве): (38) Для каждого значения оно принимает ряд значений: ( т.е. всего значений (2l+1). Все выше сказанное означает, что если атом водорода находится в каком-либо стационарном состоянии, характеризуется главным квантовым числом n (энергия En), то электрон может иметь n возможных значений модуля вектора орбитального момента Ll, в том числе и нулевое значение. При этом вектор Ll может иметь (2l+1) возможных ориентаций относительно оси z, что определяется значением магнитного орбитального квантового числа ml (пространственное квантование). Кроме орбитального момента Ll импульса, электрон обладает собственным моментом импульса Ls , который назван “спин”. Модуль этого вектора определяется: ( где: s - спиновое квантовое число, имеющее единственое значение 1/2. Проекции спина на ось определяются: ( где: ms - магнитное спиновое квантовое число, имеющее два значения 1/2, т.е. вектор Ls относительно оси z может ориентироваться только двумя способами. Таким образом, при данном значении n (т.е. задана энергия En) атом водорода имеет число состояний: (42) Так как энергия атома водорода определяется только значением (добавочная энергия, обусловленная тонким и сверхтонким взаимодействием пока не учитывается), то уровни можно считать 2n2 - кратно вырожденными. |
