атомная физика на английском. Методическое пособие по лабораторному практикуму Атомная физика часть 1 для студентов 3 5 курсов физического факультета
 Скачать 0.88 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра экспериментальной физики Методическое пособие по лабораторному практикуму «Атомная физика» часть - 1 для студентов 3 - 5 курсов физического факультета Кемерово 2003 Методическое пособие по лабораторному практикуму «Атомная физика», часть - 1 Кемерово 2003.- с.
Пособие предназначено для студентов 3-5 курсов физического факультета университета.
Кемеровский государственный университет, 2003 г. СОДЕРЖАНИЕ ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА. ЗАКОН СТЕФАНА- БОЛЬЦМАНА 4 ОПРЕДЕЛЕНИЕ РЕЗОНАНСНОГО ПОТЕНЦИАЛА МЕТОДОМ ФРАНКА-ГЕРЦА 23 ЗАКОНЫ ВНЕШНЕГО ФОТОЭФФЕКТА 38 ИЗУЧЕНИЕ СПЕКТРА АТОМА ВОДОРОДА 59 ЛАБОРАТОРНАЯ РАБОТА № - 1 ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА. ЗАКОН СТЕФАНА-БОЛЬЦМАНА Методические указания к лабораторному практикуму ЦЕЛЬ РАБОТЫИзучение законов излучения абсолютно черного тел, определение значения постоянной Стефана-Больцмана. Содержание. 1. Введение. 2. Энергетические характеристики излучения. 3. Оптические свойства черного тела. Закон Стефана-Больцмана. 4. Излучение реальных тел. Закон Киргофа. 5. Методика экспериментального изучения теплового излучения. 6. Устройство и технические характеристики установки. 7. Правила техники безопасности. 8. Порядок выполнения работы. 9. Контрольные вопросы. 10. Литература. 1. ВВЕДЕНИЕ Любое тело при температуре (Т) испускает электромагнитное излучение, называемое тепловым (температурным). В энергию излучения превращается внутренняя энергия тела: хаотическое тепловое движение возбуждает атомы и молекулы, которые при переходе в основное энергетическое состояние испускают кванты электромагнитного поля. Из всех видов излучений только тепловое может находиться в термодинамическом равновесии с веществом (состоянии). С увеличением температуры мощность излучения резко возрастает, а спектр излучения (сплошной) сдвигается в область коротких волн. Тепловое излучение имеет место в основном в оптическом диапазоне 0,01…1000 мкм, который подразделяют на три части: видимое излучение (0,4…0,76 мкм), инфракрасное (ИК) длиннее 0,76 мкм и ультрафиолетовое (УФ) короче 0,4 мкм. 2. Энергетические характеристики излучения. Различают энергетические и спектральные характеристики оптического излучения. Спектральные величины, в отличие от интегральных, рассматривают распределение энергии на различных частотах. Рассмотрим сначала интегральные характеристики оптического излучения. Поток излучения (мощность) записывается в виде =W/t, где W - энергия излучения за время t. Измеряется в ваттах, (Вт). Излучательность (энергетическая светимость) R – величина, равная потоку излучения, испускаемого с единицы площади тела по всем направлениям в полусферу R=/S, где поток излучения с площади S. R измеряется в ваттах на квадратный метр (Вт/м2). Следовательно, поток излучения с площади S равен  (1)а испущенная за время t энергия W=t=RSt. Рассмотрим теперь угловую характеристику излучения – зависимость излучения от угла между направлением света и нормалью n к поверхности (рис.1а). Пусть с площади S под углом испускается в телесном угле d поток излучения d (рис. 1б). Лучистость (энергетическая яркость) поверхности есть величина  (2) 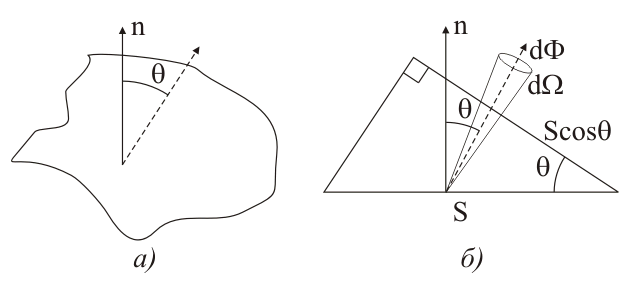 Рисунок 1. Из рис. 1б видно, что Scos – “кажущаяся площадь” излучателя под углом наблюдения . B измеряется в ваттах на стерадиан метр в квадрате (Вт/(срм2)). Распределение энергии излучения по спектру может быть представлено в виде некоторых функций частоты или длины волны излучения (мы будем пользоваться зависимостями от длины волны). Например, если в интервале длин волн , +d иcпускается поток d, то величина =d/d называется спектральной плотностью потока излучения. измеряется в ваттах на метр (Вт/м), зависит от и численно равна мощности излучения в единичном интервале длин волн. Аналогичная характеристика, но с единицей площади, есть испускательная способность (спектральная плотность излучения)  (3) R измеряется в ваттах на кубический метр (Вт/м3). В интервале длин волн от до +d, поток излучения равен 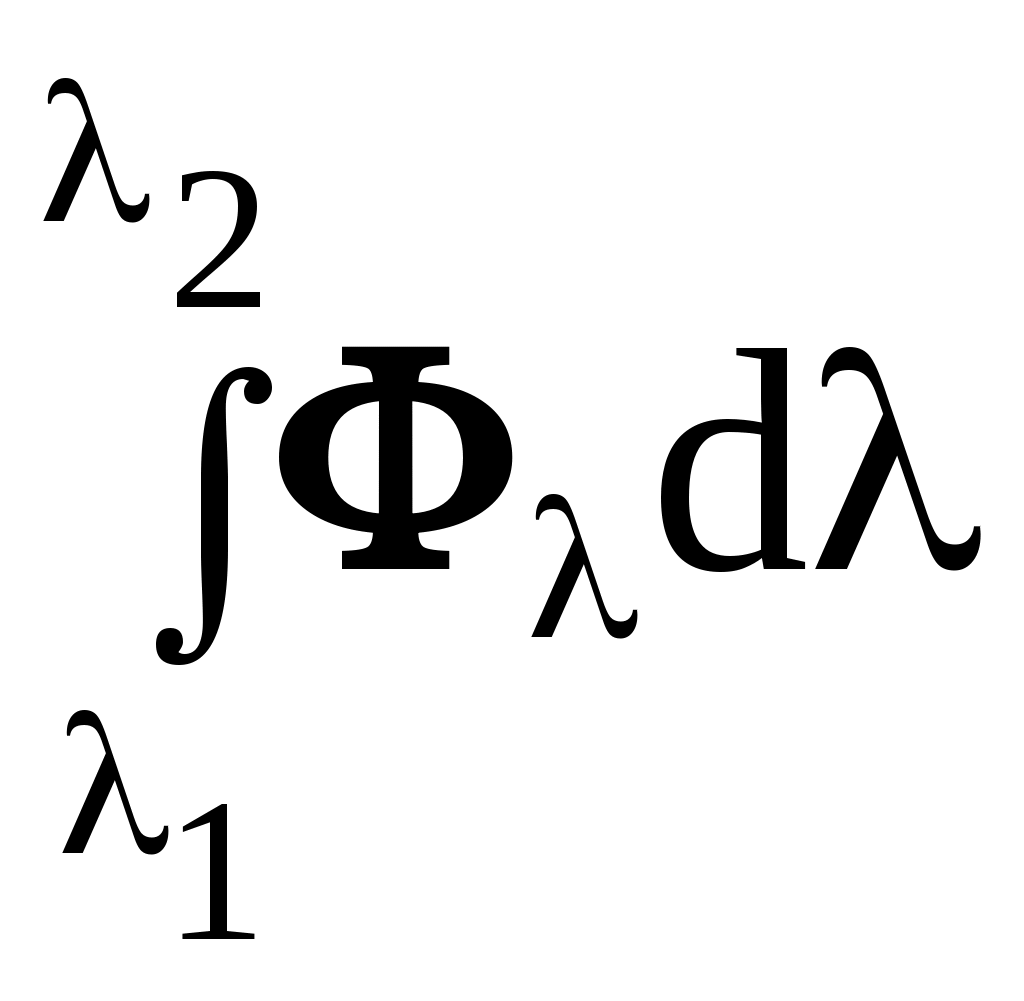 полный поток  Аналогичное соотношение  Вернемся к интегральным характеристикам. Для большинства светящиихся тел яркость (излучательность) зависит от угла наблюдения: B=B(). Д  ля некоторых тел (молочное стекло и др.) яркость примерно одинаковая в различных направлениях. (4)Тогда поток излучения пропорционален косинусу угла (см. формулу (2)): (  5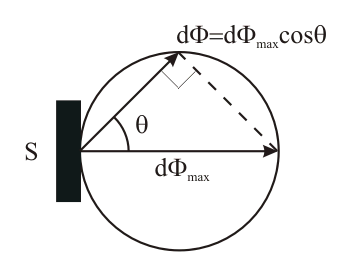)г  де dmax=BSd – поток в направлении нормали.Рисунок 2. Зависимость (5), изображенную в полярных координатах (рис. 2), называют законом Ламберта (а соответствующие излучатели – ламбертовскими или косинусными). Этот закон выполняется точно лишь для маленького излучающего отверстия в стенке равномерно раскаленной полости – так называемого “черного тела”, играющего важную роль в физике теплового излучения. Д  ля ламбертовского источника излучательность R и лучистость B связаны соотношением (6) которое можно получить интегрированием потока излучения (5) по различным направлениям в полусферу (в пределах телесного угла 2 стерадиан). 3. Оптические свойства черного тела. Падающий на тело поток излучения делится на три части – отраженную (отр), поглощенную (погл) и пропущенную сквозь тело (проп): (  7)Для монохроматического излучения спектральными коэффициентами отражения, поглощения и пропускания называют отношения  (8) Э  ти безразмерные коэффициенты, изменяющиеся от 0 до 1, зависят от вещества, состояния поверхности, длины волны, температуры тела. Коэффициент поглощения – называют также поглощательной способностью тела. Из (7), (8) следует соотношение(9) Тело поглощающее весь падающий на него поток излучения, независимо от длины волны и температуры, называется абсолютно черным телом (АЧТ). Для него aчерн,T=1. 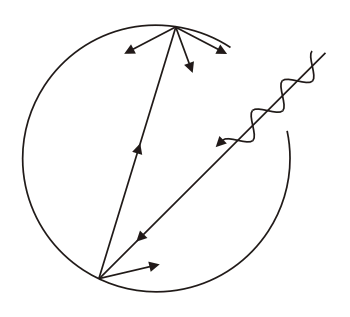 Рисунок 3. Рис. 3 Строго говоря, АЧТ – научная абстракция, таких тел нет в природе. Однако в ограниченном спектральном интервале многие тела близки к АЧТ, особенно маленькое отверстие в стенке большой замкнутой полости, стенки которой непрозрачны и имеют одинаковую температуру (рис. 3). Только незначительная часть проникшего в полость излучения выйдет наружу. Отверстие в полости служит экспериментальной моделью АЧТ (для краткости, черное тело) и используется в оптике. Наряду с понятием АЧТ используют понятие серого тела, поглощательная способность меньше единицы, но примерно одинакова для всех длин волн (в некоторой, существенной для данного рассмотрения области спектра): aсерT=aT<1. Для серого тела aT зависит от материала, состояния поверхности и температуры. 4. Излучение АЧТ и реальных тел. Согласно теоретическому выводу Кирхгофа, испускательная способность абсолютно черного тела зависит только от его температуры и длины волны. Это означает, что излучение из маленького отверстия нагретой полости не зависит от свойств вещества стенок полости. Это обстоятельство – принципиальное и ставит изучение АЧТ в выделенное положение и в теории, и на практике. Излучение АЧТ описывается более простыми и точными законами, чем излучение других тел. Модели АЧТ используются в качестве эталонного источника с известными свойствами. Закон излучения Планка (основной закон тепловых излучений): испускательная способность АЧТ (rT) зависит от длины волны и температуры следующим образом: ( 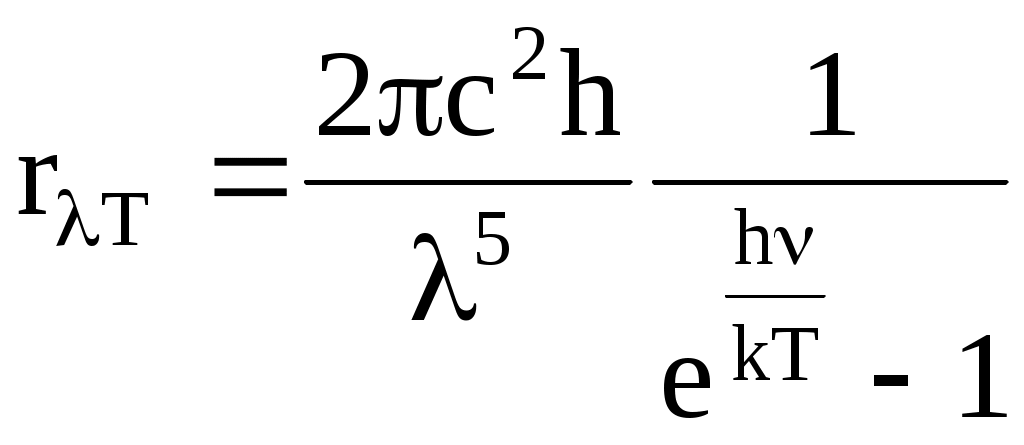 10)г 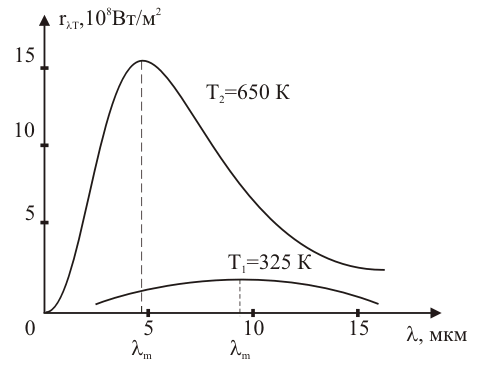 де c - скорость света в пустоте, k – постоянная Больцмана, h – постоянная Планка.Рисунок 4. При выводе (9) Планк выдвинул квантовую гипотезу, согласно которой атомные осцилляторы излучают энергию не непрерывно, а опрделенными порциями – квантами, причем энергия кванта пропорциональна частоте излучения E=h. Зависимость rT от при T=const описывает спектром излучения. На рис. 4 представлены спектры при некоторых значениях температуры. Мощность излучения с единичной площади в узкой спектральной полосе ширины d. т. е. величина rTd имеет максимум при некотором значении =max, которое уменьшается с увеличением температуры. 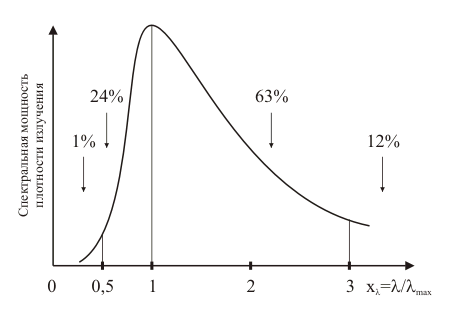 Рисунок 5. Рис. 5 Х 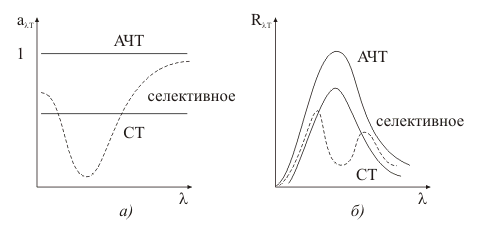 отя спектр изменяется с изменением температуры, он имеет общие закономерности, не зависящие от T, если выразить волны в безразмерной единице x=/max. Тогда доля излучаемой энергии в различных участках не зависит от температуры (доля в % от полной энергии приведена на рис. 5). Полезно запомнить, что примерно 90% энергии приходится на спектральный интервал x=0,5…3,0 ,т.е. от max/2 до 3max.Рисунок 6. Формула (9) и закон Ламберта (5) полностью описывает излучение АЧТ. Из (9) можно получить ряд полезных следствий, например закон Стефана – Больцмана и закон смещения Вина (открыты ранее закона излучения Планка). З  акон смещения Вина. Длина волны max, соответствующая максимальной спектральной плотности излучательности АЧТ, обратно пропорциональна температуре: (11)где C – постоянная. Ф  ормулу (10) и значение C=hc/(4,965K)=2,910-3 Км можно получить, если продифференцировать функцию (9) по и приравнять производную нулю:(12) ЗАКОН СТЕФАНА-БОЛЬЦМАНА. Излучательность АЧТ, т.е. полная мощность излучения с единичной площади, пропорциональна четвертой степени температуры  (13) где =(25k4)/(15c2h3) есть постоянная Стефана – Больцмана (одна из фундаментальных физических постоянных). Значения max и RЭ (округленные) для различной температуры АЧТ приведены в табл. 1 Таблица 1.
Излучение реальных тел отличается от излучения АЧТ по мощности, спектру и угловому распределению. Закон Кирхгофа (рис. 6). Для всех тел отношение испускательной способности RT к поглощательной способности aT равно испускательной способности rT абсолютно черного тела при той же температуре и длине волны, причем rT (см. формулу (9)) является универсальной функцией и T  (14) Из формулы (12) следует, что излучение реальных тел RT=aTrT меньше, чем АЧТ при одинаковых и T, так как aT<1. Если тело плохо поглощает излучение (хорошо отражает или прозрачно), то оно будет слабо светиться на этих же длинах волн. На рис. 6а представлены спектры поглощения абсолютно черного тела, серого тела (СТ) и тела с селективным (избирательным) поглощением, т.е. зависящим от . Спектры теплового излучения этих тел при одинаковой температуре изображены на рис. 6б. На всех длинах волн излучение серого тела составляет постоянную долю aT<1 от излучения АЧТ, т.е. серый спектр подобен черному. Для тела с селективным поглощением спектр излучения может быть совсем иным. Излучательность RTсер серого тела, согласно закону Кирхгофа, равна RTсер=aTrT, а полная мощность с единичной площади  и  ли с учетом (11) (14)Таким образом, закон Стефана – Больцмана (11) можно применять к серым телам, введя поправочный множитель aT. Коэффициент поглощения aT в (13) называют также коэффициентом излучения серого тела (или коэффициентом черноты). 5. Методика экспериментального изучения теплового излучения. Для черного тела запишем (см. формулу (1), (11)) полн=SизлT4. Чтобы найти , нало для черноты тела площади Sизл измерить температуру T и полный поток излучения полн (по всем направлениям и частотам), причем в определенных (абсолютных) единицах – ваттах. Такого рода измерения относятся к абсолютным измерениям и представляют определенную сложность. Для черного тела полный поток излучения в полусферу полн можно найти, если измерить поток в небольшом телесном угле и воспользоваться законом Ламберта, т.е. известной зависимостью излучения от угла (формула (5) и рис . 2). 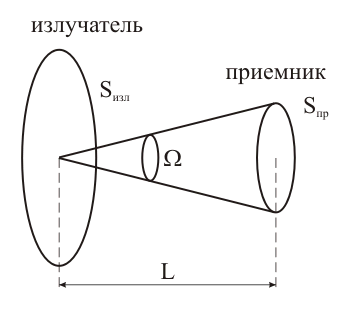 Рисунок 7. П  ри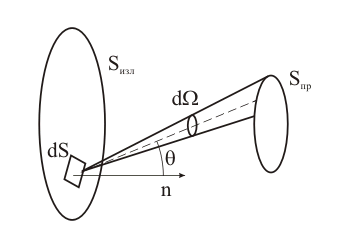нципиальная схема измерений дана на рис. 7. Излучатель площади Sизл, имеющий лучистость (энергетическую яркость) B и излучательность R, дает полный поток излучения по всем направлениям (см. формулы (1), (6))(  16)  Рисунок 8. Излучение измеряется приемником с площадью приемного элемента Sпр. Поток излучения с поверхности dS, в телесном угле d, под углом (рис. 8) равен (см. формулу (5))  П 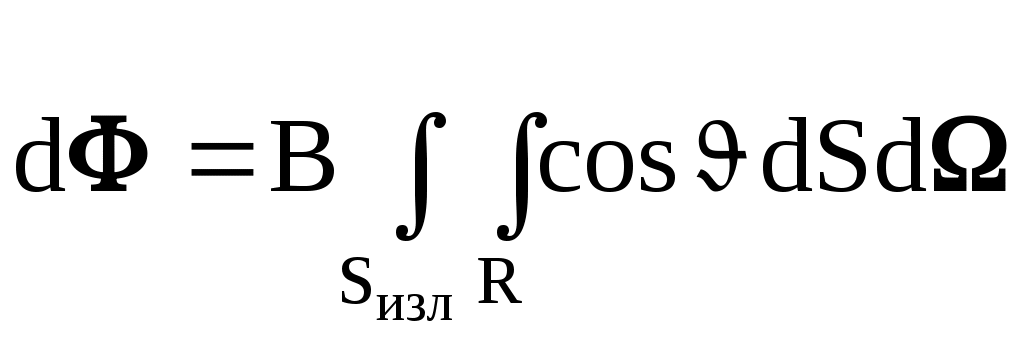 оток излучения в телесном угле падающий на приемник, равен(17) г  де интегрирование производится по площади излучателя Sизл и по всем углам в направлении приемника. Интеграл находится просто для случая, когда линейные размеры излучателя и приемника малы по сравнению с расстоянием L между ними. Тогда угол мал (cos1), телесный угол равен =Sпр/L2 и из (15) получим:(18) Напомним, что телесный угол с вершиной в центре сферы равен отношению площади, вырезаемой образующими угла на поверхности сферы, к квадрату радиуса сферы. И  сключая B из (14) и (16), получим искомое соотношение между потоками:(19) По закону Стефана – Больцмана для серого тела (15)  (20) И  сключим Фполн из (17) и (18), тогда (21)SизлaTT4 - полная мощность излучения с площади Sизл, серого тела при температуре T, а множитель (Sпр/L2) - это доля излучения, попадающего в приемник. В данной работе температура излучателя изменяется от комнатной (22 C или Т0=295 К) до Т900 К. При комнатной температуре Т0 на приемник со стороны излучателя падает поток (19) (  21а)С  ледовательно, при возрастании температуры от Т0 до Т поток излучения возрастает на величину(22) Выражение (20) - главное для экспериментальной части работы. Принимаемое излучение приемник преобразует в выходное напряжение U, которое пропорционально приращению потока (при малых ): (  23)Коэффициент преобразования (чувствительность) можно измерять с помощью калибровки. Зависимость (21) изображена на рис. 9. То обстоятельство, что "отклик" приемника U пропорционален , а не самому потоку , обусловлено принципом действия приемника. 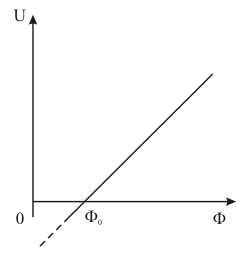 Рисунок 9.Другое важное свойство приемника - примерно одинаковая чувствительность к излучению различной частоты, испускаемому нагретыми телами. Тепловой спектр широкий (по крайней мере от 0,5max до 3max), и все его составляющие должны преобразовываться в выходной сигнал с одинаковым значением . |