Методическое пособие по выполнению практических работ по предмет. Методическое пособие по выполнению практических работ по дисциплине Теория вероятностей и математическая статистика

• Название: Методическое пособие по выполнению практических работ по дисциплине Теория вероятностей и математическая статистика
• Дата: 02.06.2022
• Размер: 1.23 Mb.
• Имя файла: Методическое пособие по выполнению практических работ по предмет.doc
• Тип: Методическое пособие; #566144
• страница: 7 из 8

Практическая работа №8 «Вычисление функции и плотности распределения непрерывных случайных величин».

Случайная величина – величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента.

Непрерывной назовём случайную величину, которая может принять любое значение из некоторого промежутка.

Распределение вероятностей непрерывной случайной величины х можно задавать либо функцией распределения F(x)=p(ξ , называемой плотностью вероятности.

Зная F(x), можно найти плотность вероятности по формуле:

f(x)=F'(x),

а зная f(x), найдём функцию распределения:



Для непрерывной случайной величины х вероятность попадания её в промежуток с концами a и b равна:

.

Причём .

Пример. Задана следующая функция распределения:



Найти плотность распределения.

Решение.

Зная F(x), можно найти плотность вероятности по формуле:

f(x)=F'(x)=
Равномерное распределение. Случайная величина х называется равномерно распределённой на [a, b], если её плотность распределения f(x) на [a, b] постоянна, а вне [a, b] равна 0:

,
Пример 1. Время ожидания автобуса (х) измеряется в минутах и распределено равномерно на отрезке [0, 30]. Определить, что ждать придётся не более 10 минут.

Решение.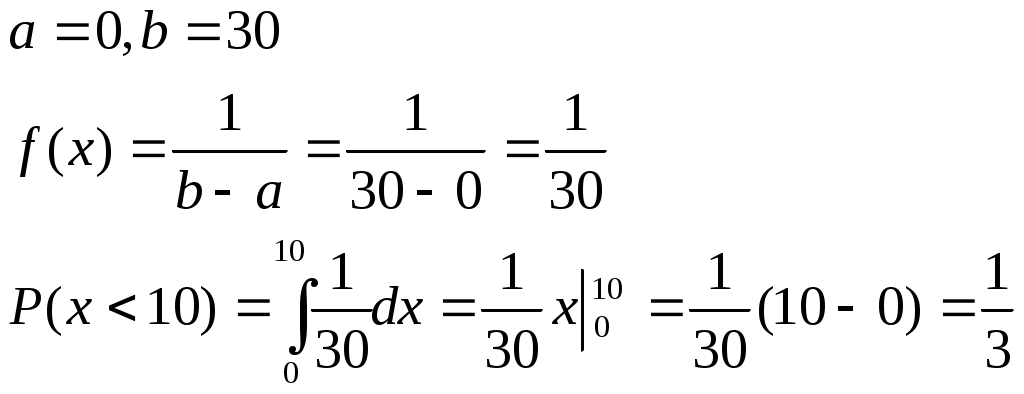


Пример 2. Задана плотность распределения:

Найти h.

Решение.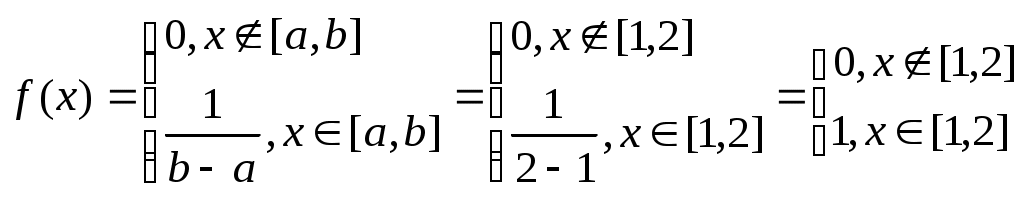

h-2=1  h=3

Нормальное распределение. Случайная величина х называется нормально распределённой, если её плотность распределения f(x) имеет вид:

,

где а и σ – параметры нормального распределения, σ >0.

В этом случае говорят, что х распределено нормально согласно закону N(a, σ).

Если а=0 и σ=1, то и эта функция обозначается через φ(х) и называется плотностью нормированного и центрированного нормального распределения. Функция распределения в этом случае обозначается через .

Значения Ф(х) затабулированы, .
Пример. Рост мужчины в Москве имеет нормальное распределение. Средний рост мужчины в Москве а=175 см, σ=10 см. Какова вероятность, что рост первого встречного мужчины будет в пределах 160-190 см?

Решение.



Правило трёх сигм. Случайная величина х распределена нормально N(a, σ).



Пример. Рост мужчины в Москве имеет нормальное распределение. Средний рост мужчины в Москве а=175 см, σ=10 см. Какова вероятность, что рост первого встречного мужчины будет в пределах 145-205 см?

Решение.



Правило двух сигм. Случайная величина х распределена нормально N(a, σ).



Правило одной сигмы. Случайная величина х распределена нормально N(a, σ).

Практическая работа №9 «Вычисление числовых характеристик важнейших непрерывных распределений».

Математическое ожидание непрерывной случайной величины определяется по формуле:

.

Дисперсия непрерывной случайной величины определяется по формуле:

.

Свойства математического ожидания и дисперсии дискретных случайных величин справедливы и для непрерывных случайных величин.
Равномерное распределение.

Пример. Время ожидания автобуса (х) измеряется в минутах и распределено равномерно на отрезке [0, 30]. Определить среднее время ожидания автобуса и дисперсию.

Решение.

Практическая работа №10 «Вычисление плотности распределения одного случайного аргумента».

Функцией распределения двумерной случайной величины (X, Y) называют вероятность совместного выполнения двух неравенств:

F(x, y) = P{X<x, Y<y}.

Плотность распределения двумерной случайной величины вычисляется как вторая смешанная частная производная функции распределения:

f(x,y) = F_xy(x,y).
Выражение функции распределения через плотность:



Свойства плотности распределения.

1. 
   Плотность распределения двумерного случайного вектора есть функция неотрицательная: f(x,y) 0.
   
2. 
   Двойной интеграл в бесконечных пределах от плотности распределения двумерного случайного вектора равен единице:
   

3. 
   Плотности распределения компонент случайного вектора могут быть получены по формулам:
   

,

Закон распределения дискретного случайного вектора (X, Y) – это совокупность всех возможных значений случайного вектора (X, Y) и их вероятностей:

p_ij=P{X=x_i, Y=y_j}, где i=1, 2, …, n, j=1, 2, …, m.

n, m – число возможных значений случайных величин X и Y.

Так же, как и в непрерывном случае:

, , .

Пример 1. Качество продукции характеризуется двумя случайными величинами: X и Y. Закон распределения случайного вектора (X,Y) представлен в таблице:

yj xi	0	0,1	0,2	0,3	pi
5	0,2	0,1	0,05	0,05	0,4
6	0	0,15	0,15	0,1	0,4
7	0	0	0,1	0,1	0,2
pj	0,2	0,25	0,3	0,25

На пересечении i-той строки и j-того столбца таблицы находятся вероятности p_ij=P{X=x_i, Y=y_j}.

Найти закон распределения координат X и Y случайного вектора.

Решение. Вероятность события {X=x_i}=p_i, есть сумма вероятностей, находящихся в i-той строке. Вероятности p_i находятся в последнем столбце таблицы.

Ряд распределения случайной величины X имеет вид:

xi	5	6	7
pi	0,4	0,4	0,2

Ряд распределения Y находим, вычисляя суммы элементов столбцов таблицы. Эти вероятности p_j находятся в последней строке таблицы.

Ряд распределения случайной величины Y имеет вид:

yj	0	0,1	0,2	0,3
pj	0,2	0,25	0,3	0,25

Условное распределение компонент дискретного случайного вектора (X, Y) – это ряд распределения одной случайной величины, вычисленной при условии, что другая случайная величина приняла определённое значение, а именно: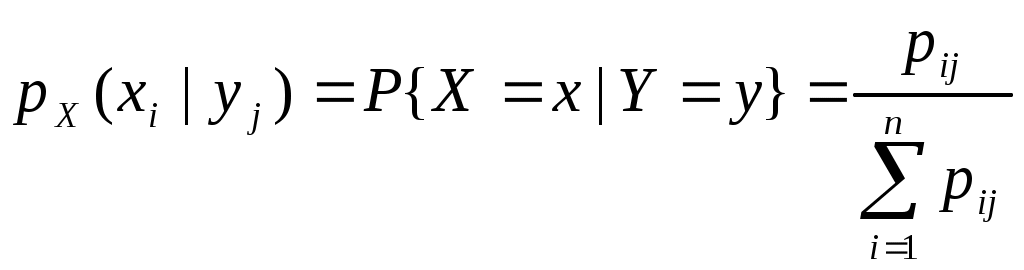

;

Пример 2. В условиях закон распределения дискретного случайного вектора (X,Y) из примера 1, найти условное распределение случайной величины X при условии, что случайная величина Y приняла значение y₂=0,1.

Решение. Выбрав значения p_i2 из столбца таблицы, соответствующего значению y₂=0,1, и разделив их на 0,25, получаем следующее условное распределение X при условии, что Y=0,1:

xi	5	6
pX(xi|y2)	0,4	0,6

Практическая работа №11 «Построение графических изображений выборок и эмпирических функций распределения».

Для наглядного представления статистического распределения пользуются графическим изображением вариационных рядов (полигоном, гистограммой и куммулятой).

В случае дискретного распределения на оси абсцисс откладывают отдельные значения признака. Из принимаемых значений x_i проводят перпендикуляры, длины которых пропорциональны частотам m_i, затем концы соседних перпендикуляров соединяют отрезками прямых. Это полигон для дискретных вариационных рядов.

Пример. На телефонной станции проводились наблюдения над числом Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты:

Число в мин (xi)	0	1	2	3	4	5	7
Частоты (mi)	8	17	16	10	6	2	1	=60

Гистограмма строится только для интервального вариационного ряда (группированной выборки). На каждом из интервалов значений как на основании, строят прямоугольник с высотой, пропорциональной m_i. Если середины верхних сторон прямоугольников соединить отрезками прямых, а концы этой ломаной ещё соединить с серединами соседних интервалов, частоты которых равны 0, а длина равна длине соседнего интервала, то получим полигон интервального ряда.

Пример.

Выработка продавцов	Число продавцов	В процентах к итогу	Кумулятивная (накопленная) численность	Накопленная относительная частота
80-100	5	10	5	0,1
100-120	10	20	15 (5+10)	0,3
120-140	20	40	35 (15+20)	0,7
140-160	10	20	45 (35+10)	0,9
160-180	5	10	50 (45+5)	1
итого	50	100

Кумулята – график накопленных частот, сглаженное графическое изображение эмпирической функции распределения. При построении кумуляты в точке, соответствующей принимаемому значению, для дискретного ряда и в правом конце интервала для интервального ряда строится перпендикуляр, высота которого пропорциональна накопленной частоте, затем верхние концы перпендикуляров соединяются между собой с помощью прямолинейных отрезков.

«Накопленные частоты» - это и есть значения эмпирической функции распределения, а кумулята – её сглаженное графическое изображение.

Практическая работа №12 «Вычисление выборочных средней и дисперсии».

Пусть x₁, x₂, …, x_n – данные наблюдений над случайной величиной X. Средним арифметическим наблюдаемых значений случайной величины X называется частное от деления суммы всех этих значений на их число:

(1).

Если данные наблюдений представлены в виде дискретного ряда, где x₁, x₂, …, x_n – наблюдаемые варианты, а m₁, m₂, …, m_n – соответствующие им частоты, причём , то, по определению,

(2).

Вычисленное по данной формуле среднее арифметическое называется взвешенным, так как частоты m_i называются весами, а операция умножения x_i на m_i – взвешиванием.

Для интервального вариационного ряда за x_i принимают середину i-го интервала, а за m_i - соответствующую интервальную частоту:

(3).

Основные свойства среднего арифметического:

1. 
   Среднее арифметическое алгебраической суммы соответствующих друг другу значений равна алгебраической сумме средних арифметических:
   

.

2. 
   Если ряд наблюдений состоит из двух непересекающихся групп наблюдений, то среднее арифметическое всего ряда наблюдений равно взвешенному среднему арифметическому групповых средних, причём весами являются объёмы соответствующих групп:
   

.

3. 
   Среднее арифметическое постоянной равно самой постоянной:
   

4. 
   Постоянную можно выносить за знак среднего арифметического:
   

5. 
   Сумма отклонений результатов наблюдений от их среднего арифметического равна нулю:
   

6. 
   Если все результаты наблюдений увеличить (уменьшить) на одно и то же число, то среднее арифметическое увеличится (уменьшится) на то же число:
   

7. 
   Если все частоты вариантов умножить на одно и то же число, то среднее арифметическое не изменится.
   

Выборочной дисперсией значений случайной величины X называется средне арифметическое квадратов отклонений наблюдаемых значений этой величины от их среднего арифметического:

(4).

Если данные наблюдений представлены в виде дискретного ряда, где x₁, x₂, …, x_n – наблюдаемые варианты, а m₁, m₂, …, m_n – соответствующие им частоты, причём 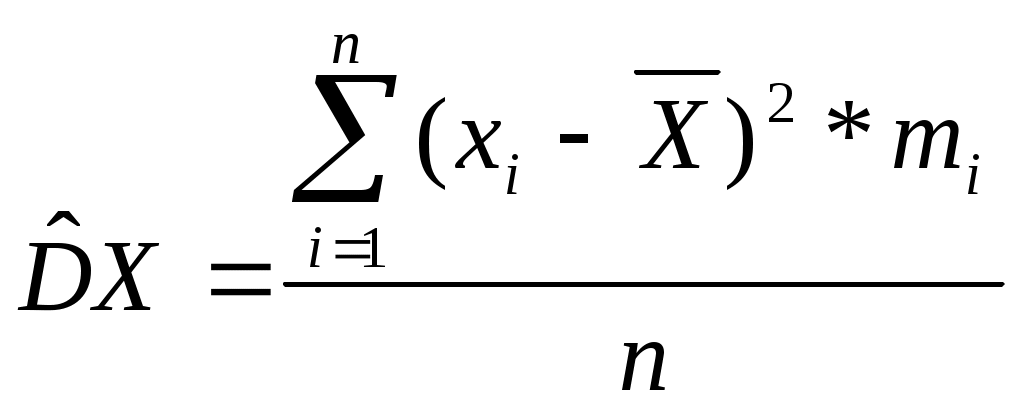, то выборочная дисперсия определяется формулой:

(5).

Используя равенство , последнюю формулу можно представить в виде:

(6).

Дисперсия, вычисленная по формулам 5 и 6, называется взвешенной выборочной дисперсией.
Основные свойства выборочной дисперсии:

1. 
   Дисперсия постоянной равна нулю:
   

2. 
   Если все результаты наблюдений увеличить (уменьшить) на одно и то же число С, то дисперсия не изменится: .
   
3. 
   Если все результаты наблюдений умножить на одно и то же число С, то имеет место равенство:
   

.

4. 
   Если все частоты вариантов умножить на одно и то же число, то выборочная дисперсия не изменится.
   
5. 
   Выборочная дисперсия равна разности между средним арифметическим квадратов наблюдений над случайной величиной X и квадратом её среднего арифметического:
   

Пример 1. По данным, приведённым в таблице, вычислить среднее арифметическое и дисперсию числа неправильных соединений в минуту.

Индекс	i	1	2	3	4	5	6	7
Число неправильных соединений в минуту	xi	0	1	2	3	4	5	7
Частота	mi	8	17	16	10	6	2	1
частость		8/60	17/60	16/60	10/60	6/60	2/60	1/60

Решение. Среднее арифметическое вычислим по формуле 2:



Дисперсию вычисляем по формуле 5:



Пример 2. По данным, приведённым в таблице, вычислить среднее арифметическое и дисперсию диаметра валика.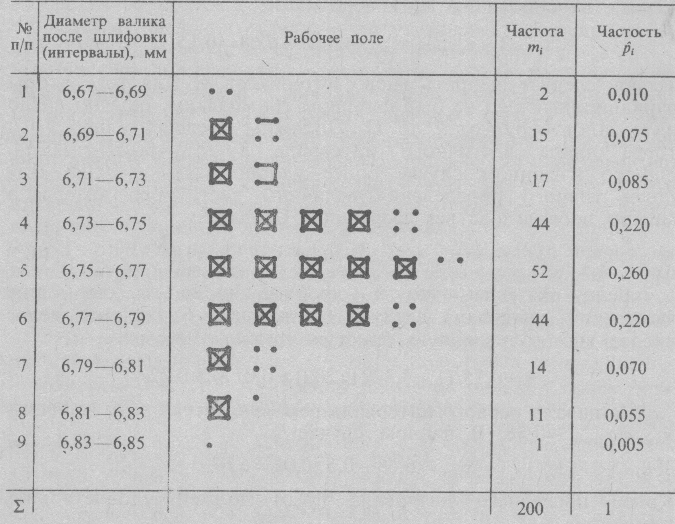


Решение. Среднее арифметическое вычислим по формуле 3:



Дисперсию вычисляем по формуле 6:

Практическая работа №13 «Решение задач на доверительный интервал».

Если в процессе эксперимента для статистики получено некоторое значение, то значит оно принадлежит области I_, вероятность которой близка к 1. Эту вероятность называют доверительной вероятностью. Её обозначают . По ней строят интервал, накрывающий значение оцениваемого параметра с вероятностью . Его и называют доверительным интервалом с уровнем доверия . Область I_ и доверительный интервал по ней строятся в соответствии с распределением вероятностей используемой статистики.

Величина уровня доверия влияет на величину интервала: чем больше уровень доверия, тем шире интервал. Уровень доверия выбирается из соображений допустимого риска.

Формула для доверительного интервала для математического ожидания  нормального распределения с уровнем доверия  для случая, когда известно среднеквадратическое отклонение распределения :

(1)

Формула для доверительного интервала для математического ожидания  нормального распределения с уровнем доверия  для случая, когда среднеквадратическое отклонение распределения  неизвестно:

(2)

Пример. Для проверки фасовочной установки были отобраны и взвешены 20 упаковок. Получены следующие результаты (в граммах):

246	247	247,3	247,4	251,7	252,5	252,6	252,8	252,8	252,9
253	253,6	254,6	254,7	254,8	256,1	256,3	256,8	257,4	259,2

Найти доверительный интервал для математического ожидания с надёжностью 0,95, предполагая, что измеряемая величина распределена нормально.

Решение. Находим точечные оценки a и :





Определяем по таблице распределения Стьюдента для доверительной вероятности =0,95 и числу степеней свободы (n-1)=19 соответствующее значение t_=2,093 и по формуле находим искомый интервал:


или 251,27 а 254,69.

Практическая работа №14 «Расчёт сводных характеристик выборки методом произведений».

Признак – это основная отличительная черта, особенность изучаемого явления или процесса. Количественное представление признака называется показателем.

Результативный признак – исследуемый показатель процесса, характеризующий эффективность процесса.

Факторный признак – показатель, влияющий на значение результативного показателя.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака (Y) от факторных (x₁, x₂, …, x_n), выражаемой в виде уравнения регрессии:

Y = f(x₁, x₂, …, x_n).

Для характеристики связей между признаками используют следующие типы функций:

- линейную ;

- гиперболическую ;

- показательную ;

- параболическую ;

- степенную .

Линейная функция используется в случае, если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, гиперболическая – если связь между Y и x, наоборот, обратная. Параболическая или степенная функция применяются, если факторный признак увеличивается в арифметической прогрессии, а результативный значительно быстрее.

Линейная однофакторная регрессия: . Для нахождения параметров a₀ и а₁ используют метод наименьших квадратов. Сущность метода заключается в нахождении параметров a₀ и а₁, при которых минимизируется сумма квадратов отклонений эмпирических значений результативного признака от теоретических, полученных по выбранному уравнению регрессии. Величину параметров a₀ и а₁ находим как решение системы нормальных уравнений:

, где n – объём исследуемой совокупности.

В уравнении регрессии свободный член регрессии коэффициент a₀ показывает совокупное влияние на результативный признак неучтённых (не выделенных для исследования) факторов; его вклад в значение результирующего показателя не зависит от изменения факторов; параметр а₁ – коэффициент регрессии – показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

Пример. По следующим данным, полагая, что зависимость между x и Y линейная, определить значения коэффициентов a₀ и а₁:

х	1	4	7	11	15	17	22
Y	3	6	10	14	18	24	30

Решение. Для определения величин a₀ и а₁ необходимо вычислить следующие значения: х, Y, xY, х². Расчёты рекомендуется проводить в Exсel и оформлять в виде таблицы:

№ п/п	х	Y	х2	xY
1	1	3	1	3	2,07
2	4	6	16	24	5,92
3	7	10	49	70	9,77
4	11	14	121	154	14,91
5	15	18	225	270	20,05
6	17	24	289	408	22,61
7	22	30	484	660	29,03
Итого	77	105	1185	1589	104,36

Система нормальных уравнений имеет вид:



Решив данную систему методом Гаусса, получаем значения: a₀=0,876, а₁=1,284. Следовательно, =0,876+1,284х. Т.к. а₁>0, связь между признаками прямая (в случае обратной связи коэффициент регрессии отрицательный). При увеличении х на единицу, - увеличивается на 1,284. Линейную модель удобно представлять графически:

Практическая работа №15 «Расчёт сводных характеристик выборки методом сумм».

Однофакторная параболическая модель второй степени - параболическая регрессия применяется, если факторный признак увеличивается в арифметической прогрессии, а результативный значительно быстрее. В этом случае уравнение регрессии будет иметь вид:

;

В данном случае задача сводится к определению неизвестных параметров: а₀, а₁,. Величину параметров a₀, а₁ и а₂ находим как решение системы нормальных уравнений:

,

Пример. По следующим данным, полагая, что зависимость между x и Y параболическая, определить значения коэффициентов a₀, а₁ и а₂:

х	1	2	3	4	5	7	10	14	17	23
Y	1	3	6	7	8	11	16	21	27	39

Решение. Для определения величин a₀, а₁ и а₂ необходимо вычислить следующие значения: х, Y, xY, х², х³, x⁴, х²Y. Расчёты рекомендуется проводить в Exсel и оформлять в виде таблицы:

№ п/п	х	Y	xY	х2	х2Y	х3	x4		= Y -
1	1	1	1	1	1	1	1	2,098	-1,098
2	2	3	6	4	12	8	16	3,488	-0,488
3	3	6	18	9	54	27	81	4,903	1,097
4	4	7	28	16	102	64	256	6,344	0,656
5	5	8	40	25	200	125	725	7,809	0,191
6	7	11	77	49	539	343	2401	10,815	0,185
7	10	16	160	100	1600	1000	10000	15,51	0,49
8	14	21	294	196	4116	2744	38416	22,13	-1,13
9	17	27	459	289	7803	4913	83521	27,36	-0,36
10	23	39	897	529	20631	12167	279841	38,5	0,5
Итого	86	139	1980	1218	35058	21392	415258

Система нормальных уравнений имеет вид:



Решив данную систему методом Гаусса, получаем значения: a₀=0,734, а₁=1,352, а₂=0,0126. Следовательно, уравнение регрессии имеет вид: =0,734+1,352х+0,0126х². Из таблицы видно, что вычисленные по уравнению регрессии значения незначительно отличаются от эмпирических данных.

Оценка обратной зависимости между Y и x, может быть дана на основе уравнения гиперболы:

Величину параметров a₀ и а₁ находим как решение системы нормальных уравнений:

,

Пример. По следующим данным, полагая, что зависимость между x и Y выражается уравнением гиперболы, определить значения коэффициентов a₀ и а₁:

х	1	3	4	6	7	9	10
Y	14	11	11	9	8	7	5

Решение. Для определения величин a₀ и а₁ расчёты рекомендуется проводить в Exсel и оформлять в виде таблицы:

№ п/п	х	Y	1/х	Y/х	1/х2		i
1	1	14	1	14	1	9,73	4,27
2	3	11	0,33	3,67	0,11	9,26	1,74
3	4	11	0,25	2,75	0,062	9,20	1,80
4	6	9	0,67	1,5	0,028	9,13	-0,13
5	7	8	0,14	1,14	0,02	9,12	-1,12
6	9	7	0,11	0,78	0,012	9,10	-2,1
7	10	5	0,10	0,5	0,01	9,09	-4,09
Итого	40	65	2,6	24,34	1,242	64,63

Система нормальных уравнений имеет вид:



Решив данную систему методом Гаусса, получаем значения: a₀=9,02, а₁=0,71. Следовательно, уравнение регрессии имеет вид: =9,02+0,71/х.