Методическое пособие язык программирования к ф. м н., доцент Мусин Наиль Минбариевич Новомосковск 2015 содержание mind Map 3 Начало работы 5
 Скачать 2.89 Mb. Скачать 2.89 Mb.
|
|
| ЧИСЛО ПРЕДПРИЯТИЙ И ОРГАНИЗАЦИЙ | | | | | | | | | | |
| (на конец года) | | | | | | | | | | |
| | 1990 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| ДФО | 16804 | 114026 | 124008 | 129957 | 133223 | 138165 | 143186 | 149239 | 157128 | 167184 |
| Республика Саха (Якутия) | 2820 | 16536 | 17455 | 17999 | 17978 | 18304 | 19341 | 20260 | 21409 | 23914 |
| Пpимоpский кpай | 3776 | 33521 | 36318 | 37826 | 38259 | 39764 | 41144 | 44404 | 47822 | 50502 |
| Хабаpовский кpай | 3386 | 20799 | 23036 | 25030 | 26386 | 28310 | 29480 | 30957 | 33355 | 36396 |
| Амуpская область | 2575 | 12272 | 13272 | 13499 | 13453 | 13674 | 14033 | 14330 | 14674 | 15124 |
| Камчатская область | 1082 | 8114 | 8916 | 9534 | 10131 | 10767 | 11460 | 12177 | 12192 | 12672 |
| Магаданская область | 1548 | 7465 | 8019 | 8379 | 8686 | 9030 | 9390 | 9738 | 9967 | 10149 |
| Сахалинская область | 1617 | 11448 | 12895 | 13675 | 14231 | 13968 | 13801 | 12689 | 12862 | 13150 |
| Еврейская АО | ... | 2745 | 2881 | 2732 | 2750 | 2870 | 2973 | 3077 | 3244 | 3499 |
| Чукотский АО | ... | 1126 | 1216 | 1283 | 1349 | 1478 | 1564 | 1607 | 1603 | 1778 |
Для удобства обработки данных выделим список территориальных единиц отдельно и далее будем работать с их номерами по списку.
| Республика Саха (Якутия) | |
| Пpимоpский кpай | |
| Хабаpовский кpай | |
| Амуpская область | |
| Камчатская область | |
| Магаданская область | |
| Сахалинская область | |
| Еврейская автономная область | |
| Чукотский автономный округ | |
| | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| | 16536 | 17455 | 17999 | 17978 | 18304 | 19341 | 20260 | 21409 | 23914 |
| | 33521 | 36318 | 37826 | 38259 | 39764 | 41144 | 44404 | 47822 | 50502 |
| | 20799 | 23036 | 25030 | 26386 | 28310 | 29480 | 30957 | 33355 | 36396 |
| | 12272 | 13272 | 13499 | 13453 | 13674 | 14033 | 14330 | 14674 | 15124 |
| | 8114 | 8916 | 9534 | 10131 | 10767 | 11460 | 12177 | 12192 | 12672 |
| | 7465 | 8019 | 8379 | 8686 | 9030 | 9390 | 9738 | 9967 | 10149 |
| | 11448 | 12895 | 13675 | 14231 | 13968 | 13801 | 12689 | 12862 | 13150 |
| | 2745 | 2881 | 2732 | 2750 | 2870 | 2973 | 3077 | 3244 | 3499 |
| | 1126 | 1216 | 1283 | 1349 | 1478 | 1564 | 1607 | 1603 | 1778 |
Создадим матрицу процентов:
> proc = matrix(nrow =9, ncol = 9)
>for (k in 1:9){proc[,k]=data[,k]/sum(data[,k])*100}
>proc=round(proc,2)
> proc
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 14.50 14.08 13.85 13.49 13.25 13.51 13.58 13.63 14.30
[2,] 29.40 29.29 29.11 28.72 28.78 28.73 29.75 30.44 30.21
[3,] 18.24 18.58 19.26 19.81 20.49 20.59 20.74 21.23 21.77
[4,] 10.76 10.70 10.39 10.10 9.90 9.80 9.60 9.34 9.05
[5,] 7.12 7.19 7.34 7.60 7.79 8.00 8.16 7.76 7.58
[6,] 6.55 6.47 6.45 6.52 6.54 6.56 6.53 6.34 6.07
[7,] 10.04 10.40 10.52 10.68 10.11 9.64 8.50 8.19 7.87
[8,] 2.41 2.32 2.10 2.06 2.08 2.08 2.06 2.06 2.09
[9,] 0.99 0.98 0.99 1.01 1.07 1.09 1.08 1.02 1.06
| | 7.25 | 7.04 | 6.92 | 6.75 | 6.62 | 6.75 | 6.79 | 6.81 | 7.15 |
| | 14.70 | 14.64 | 14.55 | 14.36 | 14.39 | 14.37 | 14.88 | 15.22 | 15.10 |
| | 9.12 | 9.29 | 9.63 | 9.90 | 10.24 | 10.29 | 10.37 | 10.61 | 10.89 |
| | 5.38 | 5.35 | 5.19 | 5.05 | 4.95 | 4.90 | 4.80 | 4.67 | 4.52 |
| | 3.56 | 3.59 | 3.67 | 3.80 | 3.90 | 4.00 | 4.08 | 3.88 | 3.79 |
| | 3.27 | 3.23 | 3.22 | 3.26 | 3.27 | 3.28 | 3.26 | 3.17 | 3.04 |
| | 5.02 | 5.20 | 5.26 | 5.34 | 5.05 | 4.82 | 4.25 | 4.09 | 3.93 |
| | 1.20 | 1.16 | 1.05 | 1.03 | 1.04 | 1.04 | 1.03 | 1.03 | 1.05 |
| | 0.49 | 0.49 | 0.49 | 0.51 | 0.53 | 0.55 | 0.54 | 0.51 | 0.53 |
Формируем матрицу процентов для региона в целом:
> years=c(1995:2003)
> region=c(1:9)
> for (k in 1:9){region[k]=sum(data[,k])/sum(data)*100}
> region
[1] 9.08 9.87 10.35 10.61 11.00 11.40 11.88 12.51 13.31
> plot(years, region)
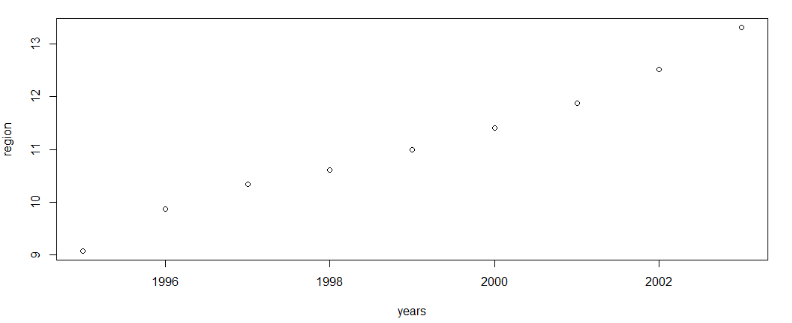
Доля малых предприятий в Дальневосточном федеральном округе монотонно увеличивается.
Рассмотрим возможные модели для нашей задачи.
Линейная модель
> summary(lm(regionyears))
Call:
lm(formula = region years)
Residuals:
Min 1Q Median 3Q Max
-0.19039 -0.11956 -0.03672 0.19228 0.28511
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -944.74294 49.40579 -19.12 2.66e-07 ***
years 0.47817 0.02472 19.35 2.46e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1914 on 7 degrees of freedom
Multiple R-squared: 0.9816, Adjusted R-squared: 0.979
F-statistic: 374.3 on 1 and 7 DF, p-value: 2.457e-07
Мера определенности (Multiple R-squared) для линейной модели составляет
Уравнение имеет вид
region = -944.74 + 0.47817∙years
Экспоненциальная модель
> summary(lm(log(region)years))
Call:
lm(formula = log(region) years)
Residuals:
Min 1Q Median 3Q Max
-0.023117 -0.011279 -0.003857 0.014203 0.021515
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -83.835347 4.185390 -20.03 1.93e-07 ***
years 0.043140 0.002094 20.60 1.59e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01622 on 7 degrees of freedom
Multiple R-squared: 0.9838, Adjusted R-squared: 0.9815
F-statistic: 424.5 on 1 and 7 DF, p-value: 1.592e-07
Мера определенности (Multiple R-squared) для линейной модели составляет
Уравнение
Степенная модель
> summary(lm(log(region)log(years)))
Call:
lm(formula = log(region) log(years))
Residuals:
Min 1Q Median 3Q Max
-0.023016 -0.011340 -0.003928 0.014304 0.021486
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -653.034 31.810 -20.53 1.63e-07 ***
log(years) 86.237 4.185 20.61 1.59e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01622 on 7 degrees of freedom
Multiple R-squared: 0.9838, Adjusted R-squared: 0.9815
F-statistic: 424.6 on 1 and 7 DF, p-value: 1.592e-07
Мера определенности (Multiple R-squared) для линейной модели составляет
Уравнение
Гиперболическая модель
Call:
lm(formula = region t)
Residuals:
Min 1Q Median 3Q Max
-0.19171 -0.11745 -0.03606 0.19274 0.28747
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.669e+02 4.958e+01 19.50 2.33e-07 ***
t -1.911e+06 9.912e+04 -19.28 2.52e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1921 on 7 degrees of freedom
Multiple R-squared: 0.9815, Adjusted R-squared: 0.9789
F-statistic: 371.6 on 1 and 7 DF, p-value: 2.52e-07
Среднеквадратичное отклонение (Adjusted R-squared) для линейной модели составляет
Уравнение
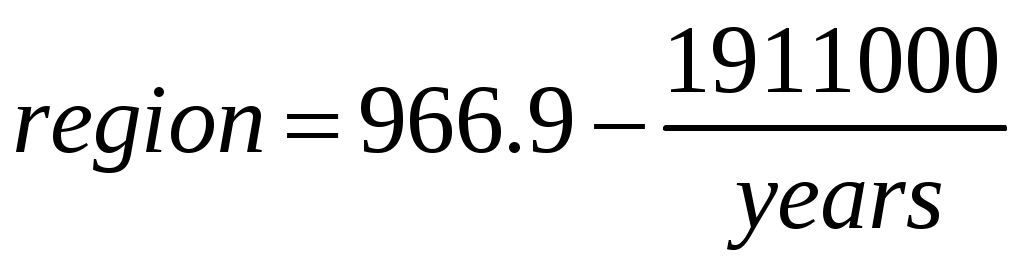
Все модели имеют высокое качество.
Наибольшее значение меры определенности имеет экспоненциальная зависимость, что дает основание рекомендовать именно ее для задач прогнозирования.
Заключение
В пособии рассмотрены конструкции самого́ языка R, которые были отобраны в результате практической обработки большого количества данных и необходимость в которых выявляется в первую очередь.
Как возникает необходимость в других конструкциях, продемонстрирована в пособии на примере решения СЛАУ и построении моделей в эконометрике.
Язык R можно с успехом применять в дальнейшем при изучении таких дисциплин, как численные методы, уравнения математической физики.
Особый интерес представляет построение баз данных. Эта тема не является предметом данного пособия, но особая эффективность и изящество конструкций языка R может быть продемонстрирована в курсах, посвященных СУБД. Первоначальные сведения об этом можно найти в [1].
Использованные источники
А.Б.Шипунов. Е.М. Балдин. П.А. Волкова. А.И. Коробейников. С.А. Назарова. С.В. Петров. В.Г. Суфиянов. – Наглядная статистика. Используем ! – М.: ДМК-Пресс. 2014.
Дьяконов А.Г. Справочник по базовым командам языка R. - http://alexanderdyakonov.narod.ru/upR.pdf
Скачано с www.znanio.ru
