вопросы по мом. Методика изучения последовательностей и их пределов. Длина окружности и площадь круга
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
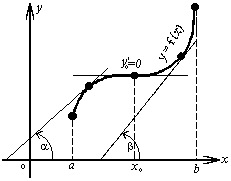
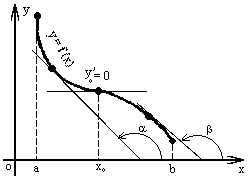
Методика изучения последовательностей и их пределов. Длина окружности и площадь круга. Методика изучения арифметической и геометрической прогрессий. Определение: числовой последовательностью наз. числовая функция натурального аргумента xn=f(n) Задать числовую последовательность значит задать правило, по которому каждому натуральному числу n соответствует одно и только одно число. Способы задания последовательности: 1)аналитический- с помощью формулы n-го члена последовательности, по которой могут быть вычислены все остальные 2)табличный 3)рекуррентный 4)словесный Виды: 1)последовательность наз.убывающей(строго) если каждый её следующий член меньше предыдущего 2) последовательность наз. возрастающей(строго) если каждый её следующий член больше предыдущего 3) последовательность наз. неубывающей если каждый её следующий член не меньше предыдущего 4) последовательность наз.не возрастающей если каждый её следующий член не больше предыдущего Прогрессии 1)Арифметической прогрессией наз. числовую последовательность, каждый член которой, начинается со второго, равен предыдущему члену, сложенному с одним и тем же числом, это число наз. разностью арифметической прогрессии и обозначают буквой d. an=a1+d(n-1) 2) Геометрической прогрессией наз. числовую последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же число, не равное нулю. bn+1=bnq Арифметическая и геометрическая прогрессии являются примерами последовательностей, изучаемых в школьном курсе,которые в свою очередь являются примерами ф-й с натуральным аргументом. Тем самым устанавливается связь этих прогрессий с ф-ми. Однако функциональный подход к прогрессиям сам по себе большого интереса не представляет, в школьном курсе дело сводиться к вычислительным задачам, решаемым на основе ф-л общего члена и суммы n членов этих прогрессий. Отдельный интерес представляет вопрос о сумме членов бесконечно убывающей геомет. прогрессии. хотя вопрос о прогрессиях дошкольного курса является традиционным тем не менее, большого применения он в нем не находит. Одно из типичных применений- вывод правил перевода бесконечной десятичной периодич.дроби в обыкновенную, которая для теперешнего базового уровня обучения, не является доступной. Предел функции и непрерывность. Понятие предела – одно из важнейших понятий курса математического анализа. Однако исторически теория пределов сформировалась позднее в 19 в, чем дифференциальное и интегральное исчисление (17в). Определение предела чрезвычайно сложно, поэтому в общеобразовательной школе можно обойтись без строгой его формулировки. Но не зависимо от того, на каком уровне вводиться понятие надо соблюдать следующее: - Проводить мотивацию изучения, например, с помощью примеров из физики, используя генетический подход, внутренние потребности самой математики. - Везде где это возможно вводить определение, сформулировать свойства и т.д., исходя из геометрически наглядных соображений, использовать графики функции. Тема начинается с изучения понятия предела числовой последовательности. Мотивацией могут служить внутренние потребности математики, так как ранее учащиеся уже сталкивались с термином предел, предельный переход. Поэтому настало время дать четкое определение этому понятию. Актуализация должна включать следующие упражнения: 1). повторение формул нахождения расстояния между 2 точкам на числовой прямой х1(х1) х2(х2) d(x1, x2) = |x1-x2| 2) показать на числовой оси множество точек удовлетворяющие равенству а) |x-a|=b б) |x-a| где a и b – фиксированные числа. 3). Решить неравенство |x – a| < b (b > 0) -b < x-a < b -b+a < x < b+a - запись окружности вокруг точки а радиуса b Далее на основе решения последних упражнений вводится понятие окружности числа (точки). Окрестность т.а радиуса b. Затем рассматривается последовательность: аn=(2n-1)/n - Выпишем несколько первых членов последовательности a1=…=1 а2=…=3/2 a3=…=5/3 …. - Изобразите полученные числа на числовой прямой (рисуем) - Можно ли указать сотый (тысячный) член этой последовательности, a1000 ? (да) a100 =1,99 a1000=1,999 - можно ли их изобразить на числовой прямой? (Можно, изображаем) - существует ли число, к которому приближаются все члены последовательности с возрастанием номера? (да к 2) - итак, при возрастании номера n члены последовательности приближаются к числу 2. Значит, расстояние между числами и числом 2 уменьшается. Найдем, например, d(a50,2) 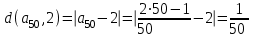 аналогично d(a100,2) - Можно ли решить обратную задачу, т.е. найти такой член последовательности (его номер n0), что d(an0, 2) < 1/200 |a0 – 2| < 1/200 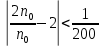 , ,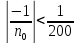 , ,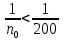 , ,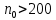 . .т.о. n0 =201, 202 ,… - Можно ли для данного расстояния найти номер? В этом случае говорят, что члены последовательности с номерами больше, чем 200 будут находиться, в окружности числа 2 с радиусом 1/200. Это записывается 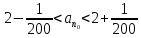 , ,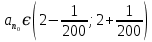 . .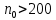 . .- Т.о. в этой окружности содержится бесконечное, число членов последовательности, а вне этой окружности – конечное множество членов, т.е. какое бы малое положительное число ε мы не задали, обязательно найдется такое число N(номер), что все члены последовательности с номерами больше, чем N будут находиться в заданной окружности числа 2 с радиусом ε. В этом случае говорят, что число 2 является пределом последовательности an. 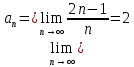 Далее рассматривается еще одна аналогичная последовательность, например: 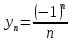 Выполняется аналогичная работа с этой последовательностью. Фактически еще раз проговаривается определение, которое далее формулируется в двух видах.
Выполняется упражнение на осознание и осмысление определения при рассмотрении конкретных числовых последовательностей. К уроку, на котором будет изучаться определение предела функций в точке, учащимся надо предложить выполнить следующее задание: 1) доказать, что lim(n-1)/3n=1/3 и т.д. 2) построить графики функций а)y=2x+1 b)y=(2x2-x-1)/(x+1), получим y=2x+1, x≠1 в) у=система: (2x2-x-1)/(x+1) при х≠1 2, при х=1 г) у=система: 2x+1, при x<1 2-x, при x  1 1На уроке вспоминается определение предела числовой последовательности и что означает неравенство |Хn - A| < ε - имеется ε-окружность точки А - А-ε < Хn < A+ε - расстояние между точками Xn и А меньше ε Мотивация. Рассматривается пример из физики:  - Если масса груза m увеличивается незначительно, то длина нити lмало изменяется. Но если масса груза близка к некоторой критической предельной массе m* (пределу прочности нити), то происходит обрыв нити. Изобразим это графически: Т 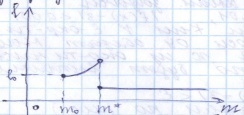 акие процессы в физике встречаются довольно часто, поэтому перед нами стоит математическая задача: акие процессы в физике встречаются довольно часто, поэтому перед нами стоит математическая задача: Найти математический аппарат (модель) с помощью которого можно описать эти процессы. Разрыв графика связан с пределом функции в точке. Рассмотрим график новой функции y = 2x+1 из д/з (строим) - С какой бы стороны (лево, право) мы по оси Ох не двигались при х →1, f(x)→3. Рассмотрим существуют ли такие значения х при которых 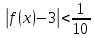 |2x + 1 – 3| < 0,1; |2x – 2| < 0,1; 2 – 0,1 < 2x < 2 + 0,1; 1,9 < 2x < 2,1 0,95 < x < 1, 05 – получилась окружность числа 1 по оси Ох. Аналогично решаются неравенства: |f(x) – 3| < 0,001, |f(x) – 3| < 0,0001 Т.е. при рассмотрение любой ε-окрестности числа 3 по оси Оу обязательно найдутся такие числа х из окрестности числа 1 по оси Ох, что будет выполнятся неравенство |f(x) – 3| < ε. (Иллюстрируют на рисунке). В этом случае говорят, что существует предел функции в точке 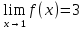 Аналогично показывается по графику другой функции. y=(2x2-x-1)/(x+1), получим y=2x+1, x≠1 (рисуем, (1, 3) – выколота). Рассуждая аналогично, получаем 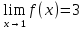 у=система: (2x2-x-1)/(x+1) при х≠1 2, при х=1 (рисуем, (2, 3) – выколота). Аналогично рассуждая полчим тот же вывод. у=система: 2x+1, при x<1 2-x, при x 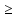 1 1(рисуем, (1, 3) – выколота). - Пусть х →1. Можно ли указать значение к которому стремится у? (Нет, нельзя, т.к. зависит от того, с какой стороны двигаемся по оси Ох). В этом случае говорят, что не существует предела функции в точке. Анализируя примеры формулируем определение. На языке ε-окресностей : Число b называется пределом функции у = f(x) при x→a , если любая ε-окрестности точки b найдется такая δ-окрестности точки а, что для всех х из этой окрестности, кроме быть может самой точки а, значения функции f(x) лежит в ε-окрестности точки b . На языке ε-δ: Число b называется пределом функции у = f(x) при x→a, если для любой ε>0, существует δ>0 ,что при всех х ≠ а, удовлетворяющих неравенству |x-a| < δ выполняется неравенство |f(x) - b|<ε. - Из приведённых определений следует, что для существования предела функции в точке, надо чтобы функция была определена во всех точках некоторой окружности данной точки, кроме быть может самой заданной точки. Для осознания и осмысления решаются задачи: 1) вставить пропущенные слова в определении 2) указать предел функции в точке 3) доказать, что функция не имеет предела в заданной точке (методом от противного). Далее по имеющимся графикам функций отвечаем на вопросы: 1) определена ли функция в точке х=1. Если да, то найти f(1) 2) существует ли предел при х→1, f(х). Если да, то указать его. 3)выполняется ли равенство lim f(x)=f(1) при x→1 Следовательно, только для функции y=2x+1 все ответы на данные вопросы положительные. И только ее график можно построить, не отрывая мел от доски. такая функции называется непрерывной, остальные разрывные. Опр. Функция y=f(x) называется непрерывной в некоторой точке а, если lim f(x) = f(a) при x→a Функция называется непрерывной на промежутке, если непрерывна в каждой точке промежутка. В учебнике Ш.А.Алимова и др. данное подробно не рассматривается, поэтому учитель сам решает в зависимости от уровня класса, на сколько углубляется в изучение данной темы. Методика введения понятия производной. Геометрический и физический смысл производной. Подходы к введению понятия производная: Логический (в классах с углубленным изучением математики): производная определяется через предел функции в точке. Исторический: производная определяется без использования понятия предела, поскольку в математике первоначально были сформированы понятия производной и интеграла, а затем, как обобщение данных понятий, понятие предела функции. Данный путь реализуется в классах общеобразовательного уровня. Для рассмотрения примеров, приводящих к определению и применению данного понятия, необходимо актуализировать следующие элементы знаний: приращение аргумента, приращение функции, свойства графика линейной функции. Определение: Производной y ' =f ' (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен. Таким образом, 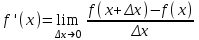 , или , или 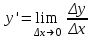 Заметим, что если при некотором значении x, например при x=a, отношение 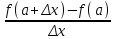 при x0 не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a. при x0 не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a. Возрастание и убывание функции. Экстремум функции. Определение 1. Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если f(x2) > f(x1) при x2 > x1.
Определение 2. Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если f(x2) < f(x1) при x2 > x1. Из этого определения следует, что у убывающей в интервале ( a, b ) функции f (x) в любой точке этого интервала приращения x и y имеют разные знаки. Определение 3. Максимумом функции f (x) называется такое значение f (x0) этой функции, которое не меньше всех значений функции f (x) в точках x, достаточно близких к точке x0 , т.е. в точках x, Значение f (x0) функции f (x), при котором выполняется вышеуказанное неравенство, называется минимальным значением функции f (x) или просто минимумом. Определение 4. Минимумом функции f (x) называется такое значение f (x0) этой функции, которое не больше всех значений функции f (x) в точках x, достаточно близких к точке x0 , т.е. в точках x, принадлежащихнекоторой достаточно малой окрестности точки x0 . Геометрический смысл производной. Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x0   f(x) 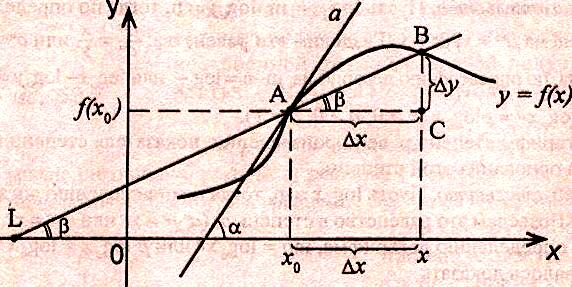 Рассмотрим произвольную прямую, проходящую через точку графика функции - точку А(x0, f (х0)) и пересекающую график в некоторой точке B(x;f(x)). Такая прямая (АВ) называется секущей. Из ∆АВС: АС = ∆x; ВС =∆у; tgβ=∆y/∆x . Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO - это угол наклона секущей АВ к положительному направлению оси Ох. Значит, tgβ = k - угловой коэффициент прямой АВ. Теперь будем уменьшать ∆х, т.е. ∆х→ 0. При этом точка В будет приближаться к точке А по графику, а секущая АВ будет поворачиваться. Предельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А. Если перейти к пределу при ∆х → 0 в равенстве tgβ =∆y/∆x, то получим 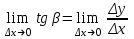 или tg =f '(x0), так как или tg =f '(x0), так как 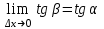 -угол наклона касательной к положительному направлению оси Ох -угол наклона касательной к положительному направлению оси Ох 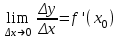 , по определению производной. Но tg = k - угловой коэффициент касательной, значит, k = tg = f '(x0). , по определению производной. Но tg = k - угловой коэффициент касательной, значит, k = tg = f '(x0).Итак, геометрический смысл производной заключается в следующем: Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0. Физический смысл производной. Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени [t0; t0+ ∆t] равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е. Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0. lim Vср (t) = (t0) - мгновенная скорость в момент времени t0, ∆t → 0. а lim = ∆x/∆t = x'(t0) (по определению производной). Итак, (t) =x'(t). Физический смысл производной заключается в следующем: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в точке x0 Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени. (t) = x'(t) - скорость, a(f) = '(t) - ускорение, или a(t) = x"(t). Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении: φ = φ(t) - изменение угла от времени, ω = φ'(t) - угловая скорость, ε = φ'(t) - угловое ускорение, или ε = φ"(t). Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня: m = m(х) - масса, x [0; l], l - длина стержня, р = m'(х) - линейная плотность. С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω2 =k/m, получим дифференциальное уравнение пружинного маятника х"(t) + ω2x(t) = 0, где ω = √k/√m частота колебаний (l/c), k - жесткость пружины (H/m). Уравнение вида у" + ω2y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решением таких уравнений является функция у = Asin(ωt + φ0) или у = Acos(ωt + φ0), где А - амплитуда колебаний, ω - циклическая частота, φ0 - начальная фаза. Общая схема исследования функции. Применение производной при исследовании функции. Понятие математического моделирования. Применение производной для нахождения наибольшего и наименьшего значения функции. Методика введения первообразной. Методика нахождения первообразных. Теме «Первообразная» предшествует тема «Первообразная и ее применение». Такая последовательность изучения материала создает предпосылки для понимания учениками взаимосвязи между операциями дифференцирования и интегрирования функций, а также основной идеи метода дифференциального и интегрального исчислений (зная функцию, можно установить характер локальной ее изменяемости в зависимости от изменения аргумента, и наоборот6 зная характер локальной изменяемости функции, можно найти либо саму функцию (при заданных начальных условиях), либо семейство функций; осознания обучающимися того факта, что аппарат производной и интеграла – основа метода математического анализа: он выступает и как язык, описывающий многие явления, процессы мира, и как инструмент, с помощью которого с учетом особенностей языка исследуются эти явления и процессы. При рассмотрении элементов интегрального исчисления реализуется идея линеаризации. С точки зрения механики скорость прямолинейного движения определяется как производная пути по времени. Если теперь рассмотреть обратную задачу – нахождения пути, пройденного точкой с заданной скоростью, то придем к функции, которую называют первообразной к исходной функции. Так как производная постоянной равна нулю, то первообразная определяется с точностью до постоянной. Если скорость меняется по закону v = v(t) и ее графиком является некоторая кривая, то путь, пройденный точкой за промежуток времени [t; t + h], приближенно равен площади прямоугольника со сторонами v(t) и h. Точное значение пути будет равно площади образовавшейся криволинейной трапеции. Если в заданную кривую v(t) вписать некоторую ломаную, то путь можно вычислить с лучшим приближением, заменив площадь криволинейной трапеции суммой площадей прямоугольников разбиения. Чем меньше будет основание прямоугольников, тем ближе сумма их площадей будет выражать площадь криволинейной трапеции. Так процесс линеаризации приводит к понятию определенного интеграла. Учебный материал строится так, что вначале вводится понятие первообразной. Таблица первообразных получается из таблицы производных. В курсе математики средней школы нет понятия неопределенного интеграла (хотя в учебнике А.Г. Мордковича этот термин используется), поэтому определенный интеграл называют просто интегралом. Введение понятия определенного интеграла осуществляется в виде предела интегральных сумм. Интегральная сумма рассматривается в общем виде (отрезки разбиения могут быть необязательно равными) и предназначена только для ознакомления с понятием интеграла. Желательно, чтобы ученики понимали, что об интегральной сумме функции на отрезке, а затем и интеграле можно говорить и в том случае, когда функция не только непрерывна и положительна, но и принимает на этом отрезке любые значения, в том числе и отрицательные, и ноль. Формула Ньютона – Лейбница вводится практически одновременно с термином «интеграл». Эта формула является главной: с ее помощью вычисляются определенные интегралы. Центральное место во всем разделе, связанном с изучением элементов интегрального исчисления, занимает вычисление площадей плоских фигур. Основной фигурой считается криволинейная трапеция. При изучении этого материала важно правильно расставлять акценты: главное здесь – построение геометрических моделей и снятие соответствующей информации с чертежа, а не вычисление интегралов. Не ради изучения интеграла считаются площади, наоборот, интеграл изучается ради вычисления площадей. Методика введения интеграла. Применение интеграла для вычисления площадей и объемов. Основная образовательная цель изучения темы "Первообразная и интеграл" может быть сформулирована так: 1) ознакомить учащихся с операцией, которая является обратной по отношению к операции дифференцирования функций; 2) познакомить с использованием метода интегрального исчисления для решения геометрических задач, некоторых задач практического содержания. В связи с этим развивающими целями будут: а) введение нового метода решения задач (в частности нахождение площади объёма фигуры) показать известную универсальность математических методов; б) показ учащимся основных этапов решения прикладных задач средствами математики. Теме "Первообразная и интеграл" предшествует тема "Производная и её применение". Такая последовательность изучения материала создаёт предпосылки для: 1) понимание учащимися взаимосвязи между операциями дифференцирования и интегрирования функций, а также основной идеи метода дифференциального и интегрального исчислений; 2) осознание учащимися того факта, что аппарат производной и интеграла - основа метода математического анализа. С одной стороны, он выступает как язык, описывающий многие явления, процессы мира. С другой - как инструмент, с помощью которого с учётом особенностей языка исследуются эти явления и процессы. Основу содержания темы составляют два типа вопросов, каждый из которых группируется около двух понятий: "Первообразная", "Интеграл". Основное внимание при изучении уделяется: 1) нахождению первообразных и вычислению интегралов на базе таблиц первообразных и правил нахождения первообразных; 2) вычислению площадей криволинейной трапеции. В качестве основных задач, решённых в процессе изучения темы, можно выделить следующие: · введение понятий первообразной и интеграла; · ознакомление учащихся с основными свойствами первообразных и правилами нахождения первообразных; · раскрытие смысла операции интегрирования как операции, обратной по отношению к операции дифференцирования заданной функции: · провести классификацию типов задач (нахождение площади криволинейной трапеции, нахождение объёма тела, задачи с физическим содержанием), показать, каким образом реализуется метод интегрального исчисления. При этом обратить внимание на выделение в процессе их решения этапов, характеризующих процесс математического моделирования. Теоретический материал включает в себя понятия первообразной и её основное свойство понятие интеграла функции; связь между понятиями "интеграл" и "первообразная", которая устанавливается с помощью формулы Ньютона-Лейбница; формула Ньютона-Лейбница как аппарат вычисления интеграла данной функции. Перечисленные понятия вводятся на дедуктивной основе, дается иллюстрация использования определения основного понятия, его свойств с помощью конкретных примеров. Задачи, помимо использования их как средства иллюстрации вводимого в рассмотрение теоретического материала, служат средством его закрепления, о чем свидетельствуют и их формулировки, например: "Найти такую первообразную функцию, график которой проходит через данную точку". Методическая схема изучения первообразной функции. В школьном учебнике были "испытаны" различные варианты введения понятия интеграла. В первых изданиях учебного пособия (под ред. А.Н. Колмогорова) интеграл определяется с помощью формулы Ньютона-Лейбница (как приращение первообразной), в более поздних изданиях применялось традиционное определение интеграла как предела интегральных сумм. Методическая схема изучения первообразной: 1) рассмотреть примеры взаимно обратных операций; 2) ввести интегрирование как операцию, обратную дифференцированию, а первообразную как результат операции интегрирования; 3) выполнить упражнения типа: "Доказать, что данная функция есть первообразная другой данной функции ", "Решить задачи на отыскание первообразной для данной функции "; 4) ознакомить учащихся с основным свойством первообразной; 5) составить таблицу первообразных; 6) ознакомить учащихся с правилами нахождения первообразных; 7) решить физические задачи с применением первообразной. Определению первообразной предшествует задача из механики: Если в начальный момент времени скорость тела равна 0, т.е., то при свободном падении тело к моменту времени пройдет путь: . Продифференцировав ее, получаем; - ускорение постоянно. Более типично для механики иное: известно ускорение точки, требуется найти закон изменения скорости и координату. Для решения таких задач служит операция интегрирования. При введении понятия первообразной пользуются аналогией с известными учащимся примерами взаимно обратных операций. Например, операция сложения позволяет по двум данным числам найти третье число - их сумму. Если же известно первое слагаемое и сумма, то второе слагаемое может быть "восстановлено" выполнением операции вычитания. Следовательно, вычитание - операция, обратная сложению, приводящая к единственному результату. Однако такое бывает не всегда. Например, возведение в квадрат числа 3 дает число 9. Пусть теперь известно, что число 9 является квадратом некоторого числа. Выполнив обратную операцию - извлечение квадратного корня - получаем два значения: 3 и -3. Дифференцирование функции приводит к новой функции, которая является производной функции Пусть теперь известно, что производная некоторой функции равна, т.е. требуется найти функцию. Операция нахождения функции по ее производной называется интегрированием. Выполняя интегрирование, можем получать следующие результаты: и т.д. Функция называется первообразными функции. Таким образом, интегрирование является операцией, обратной дифференцированию; результат операции интегрирования называется первообразной. После этого сообщается определение первообразной: функция называется первообразной для функции f(x) на заданном промежутке, если для всех x из этого промежутка. Перечисленные понятия вводятся на дедуктивной основе, дается иллюстрация использования определения основного понятия, его свойств с помощью конкретных примеров. Методика введения определения sin, cos, tg, где, а принадлежит R. Методика изучения тригонометрических функций числового аргумента. Введение тригонометрических функций начинается в старшей школе с введения элементарных понятий: числовая окружность, числовая окружность на координатной плоскости, определения синуса и косинуса числа, основное тригонометрическое тождество, определение тангенса и котангенса, тригонометрические функции числового аргумента, числовые функции углового аргумента, формулы приведения. И только после этого рассматривают функцию y=sin x, свойства и график. Свойства: D(y)=R y=sin x – нечётная y=sin x возрастает на [0;П/2], убывает на [П/2;П] ограничена снизу и сверху унаим=-1, унаиб=1 По этим свойствам строим график, таблично на [0;П], используя свойство симметричности на остальном графике. 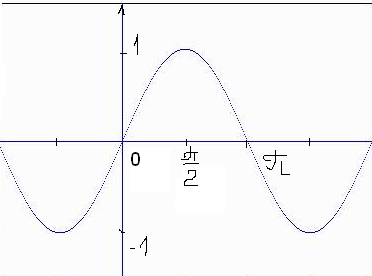 После построения: непрерывность В таком же порядке рассматриваем функцию y=cos x. Опр: Функцию f(x),xєX называют периодической, если сущ. Т≠0, что для любого xєX выполняется f(x-T)=f(x+T), T – период функции f(x), значит функции y=sin x, y=cos x – периодические. sin(x-2П)=sinx=sin(x+2П) cos(x+2П)=sinx= sin(x-2П), 2П – период функций y=sin x, y=cos x. Периодом является любое число вида kT, где k=±1;±2;±3… T – наименьший положительный период, нахождение Т по определению. Пример: Найти период функции y=sin 3x. Решение: Пусть Т – основной период f(x)=f(x+T) f(x)=sin(x) f(x+T)=sin 3(x+T)=sin (3x+3T) sin 3x=sin (3x+3T)→3T=2Пn, т.к. нужен основной период n=1 3T=2П, Т=2П/3 Основной период функции y=sin kx (y=cos kx) равен 2П/k. После изучения функций y=sin x , y=cos x знакомятся с преобразованием графиков функции y=f(x), y=mf(x), y=f(kx). Далее знакомятся с функциями y=tg x, y=ctg x. Тригонометрии в школе традиционно уделяется много внимания - сначала в курсе геометрии, затем в курсе алгебры и начал анализа. А.Г.Мордкович предлагает построить изучение темы «Тригонометрия» по следующей схеме: функция – уравнения – преобразования. Объясняется это тем, что сначала целесообразно изучить «простые модели» (таковыми являются элементарные функции), а затем переходить к изучению «сложных моделей» (таковыми в математике являются сложные выражения, которые нужно упрощать, используя формульный аппарат). Таким образом, изучение данной темы следует построить по следующей схеме: 1. рассмотрение тригонометрической формы записи действительного числа и ее свойств. Основной целью является изучить новые математические модели – числовую окружность и числовую окружность на координатной плоскости; познакомить учащихся с первым классом неалгебраических функций – тригонометрическими функциями; научить школьников находить значение тригонометрических функций некоторого аргумента по известному значению другой функции того же аргумента; дать представление о градусной и радианной мерах измерения углов. 2. Собственно тригонометрические уравнения. Основная цель – научить школьников решать простейшие тригонометрические уравнения. Сначала надо разобраться с «элементарными моделями», т.е. с простейшими тригонометрическими уравнениями и уравнениями, которые сводятся к простейшим с помощью алгебраических приемов, и только потом переходить к «сложным моделям», т.е. к уравнениям, которые надо сначала долго и упорно «раскручивать, используя рутинный аппарат формул». 3. Тригонометрическими формулами следует заняться после того, как учащиеся овладеют двумя «китами», на которых базируется курс тригонометрии: числовой окружностью и простейшими уравнениями. Основная цель – познакомить учащихся с основными тригонометрическими формулами, научить находить нужную формулу для доказательства тригонометрических тождеств, упрощения тригонометрических выражений. После того, как пройдена тема «Простейшие тригонометрические уравнения», учащимся предлагаются задания с использованием формул тригонометрии. Отсюда и вытекает для учащихся польза от изучения формул: «жуткие» уравнения принимают после преобразований вполне знакомый вид. Согласно стандарту полного общего образования в теме «Основы тригонометрии» должны быть рассмотрены следующие темы: синус, косинус, тангенс, котангенс произвольного угла; радианная мера угла; синус, косинус, тангенс, котангенс числа; основные тригонометрические тождества; формулы привидения; синус, косинус, тангенс суммы и разности двух углов; синус, косинус двойного угла; формулы половинного угла; преобразование суммы тригонометрических функций в произведение и произведения в сумму; выражение тригонометрических функций через тангенс половинного аргумента; преобразование простейших тригонометрических выражений; простейшие тригонометрические уравнения; решение тригонометрических уравнений; простейшие тригонометрические неравенства; арксинус, арккосинус, арктангенс числа; тригонометрические функции, их свойства и графики, периодичность, основной период. Методика изучения показательной и логарифмической функций. Ознакомление учащихся с показательной и логарифмической функциями начиная с изучения свойств степеней и логарифмов. Курс алгебры знакомит учащихся с понятием степени с рациональным показателем. Таким образом для любого основания степени 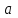 (где (где 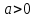 , , 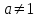 ) можно построить функцию: ) можно построить функцию: 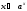 , , 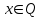 , область определения которой – множество действительных чисел. Необходимо ввести определение степени с иррациональным показателем. Используемое свойство степени с основным, например, большим единицы (возрастании), рациональное приближение иррационального числа α: r1< α< r2. Исходя из графического изображения зависимости показателя степени и значения степени, показывается, что найдется такое значение y, которое будет наибольшим среди всех ar1 и наименьшим среди всех ar2 , которое можно считать значением aα. , область определения которой – множество действительных чисел. Необходимо ввести определение степени с иррациональным показателем. Используемое свойство степени с основным, например, большим единицы (возрастании), рациональное приближение иррационального числа α: r1< α< r2. Исходя из графического изображения зависимости показателя степени и значения степени, показывается, что найдется такое значение y, которое будет наибольшим среди всех ar1 и наименьшим среди всех ar2 , которое можно считать значением aα.Затем формируется определение показательной функции: функция, заданная формулой y=ax ( 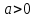 , , 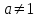 ), называется показательной функцией с основанием a, и формулируемые основные свойства: D(ax)=R; E(ax)=RТ; ax возрастает при a>1 и ax убывает при 0 ), называется показательной функцией с основанием a, и формулируемые основные свойства: D(ax)=R; E(ax)=RТ; ax возрастает при a>1 и ax убывает при 0Логарифмическая функция – новый математический объект для учащихся. К понятию логарифма учащихся подводят в процессе решения показательного уравнения ax=b в том случае, если b нельзя представить в виде степени с основанием a. Наше уравнение в случае b>0 имеет единственный корень, который называют логарифмом b по основанию a и обозначают logab, т.е. alogab=b. Одновременно с введением нового понятия учащиеся знакомятся с основным Логарифмическим тождеством. При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции: При любом 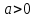 ( (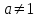 ) и любых положительных x и y, выполнены равенства: ) и любых положительных x и y, выполнены равенства:1. loga1=0 2. logaa=1 3. logaxy= logax+ logay 4. logax/y= logax- logay 5. logaxp= plogax Изучение логарифмической функции начинается с выделения определения: функцию, заданную формулой 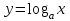 называют логарифмической функцией с основанием называют логарифмической функцией с основанием 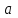 . Основные свойства выводится из свойств показательной функции: . Основные свойства выводится из свойств показательной функции:1. 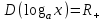 , ,2. 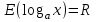 , ,3. Логарифмическая функция на всей области определения возрастает (при a>1) или убывает (при 0 Покажем, что 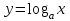 при a>1 возрастает. Пусть при a>1 возрастает. Пусть 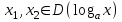 и и 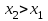 , надо доказать, что: , надо доказать, что: 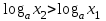 . Допустим противное, т.е. что . Допустим противное, т.е. что 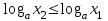 . Т.к. показательная функция . Т.к. показательная функция 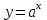 при a>1 возрастает, то из неравенства при a>1 возрастает, то из неравенства 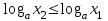 следует: следует: 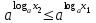 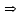 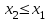 , что противоречит выбору , что противоречит выбору 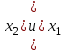 . Следовательно: . Следовательно: 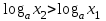 и функция и функция 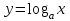 при a>1 – возрастает. при a>1 – возрастает.Т.к. при a>1 функция возрастает, то логарифмическая функция положительна при x>1 и отрицательна для 0 12.Геометрические преобразования графиков функций.  13.Методика изучения элементов комбинаторики в школе. Элементы комбинаторики — основа для вычисления вероятностей событий в широком классе вероятностных схем. Элементы методики изучения комбинаторики в школьном курсе математики были достаточно подробно разработаны, так как этот раздел изучался в школьном курсе математики в советской школе вплоть до 80-х гг. XX в. В настоящее время происходит возврат к разделу комбинаторики, так как он используется в теории вероятностей и востребован в дискретной математике, широко применяемой в различных областях знания, например в информатике. Тема «Элементы комбинаторики» может изучаться и вне контекста изучения теории вероятностей, так как она содержательно богата как в теоретическом, так и в прикладном аспектах. Основное внимание при изучении комбинаторики следует уделить задачам, поскольку объем теоретического материала чрезвычайно мал: формулы комбинаций без повторений (перестановки, сочетания, размещения). Вопрос о необходимости аккуратного вывода формул на уроках решается учителем в соответствии с логикой используемого учебника и уровнем подготовки учеников. Возможен и вариант, когда формула появляется как обобщение результата конкретной задачи. Основные проблемы возникают у учителя и школьников при решении комбинаторных задач. Они преодолеваются за счет правильно составленного набора задач по теме и обучения поиску решения (выбору соответствующей формулы). Прежде всего в набор должны быть включены несложные модельные задачи, которые позволяют решить их «вручную» — перебором всех возможных вариантов (составлением дерева вариантов). Такой способ решения позволит в дальнейшем при вычислении классической вероятности наступления события «вручную» составить пространство элементарных исходов. Подобные задачи можно найти в объяснительном тексте любого учебника. Для обучения выбору формулы можно рассмотреть с учениками следующие задачи. Задачи: В турнире участвуют 5 человек. Сколькими способами могут распределиться места между ними? Сколькими способами можно выбрать 3 ленты разных цветов из 5 лент разных цветов? Сколько трехзначных чисел можно составить из цифр 1; 2; 3; 4, если цифры в записи чисел не повторяются? Решив эти задачи с учениками, учитель делает вывод о выборе формул при решении комбинаторных задач: если в каждой комбинации участвуют все элементы множества, то это перестановки (задача 22.1). Если каждая комбинация состоит из некоторых элементов множества, то это — сочетания или размещения (задачи 22.2 и 22.3). Если в таких комбинациях важен порядок, то это — размещение (задача 22.3). Если нет, то сочетание (задача 22.2). После чего можно рассмотреть более содержательные задачи на комбинации, например такую. Задачи: Сколько четырехзначных чисел можно составить из цифр 0; 2; 5; 7; 8; 9, если цифры в записи чисел нс повторяются? В этой задаче нужно из числа размещений исключить те, первый элемент которых является нулем. Для введения правил сложения и умножения можно использовать следующие простейшие задачи. Задачи: Сколько существует способов выбора одного карандаша из коробки, содержащей 5 красных, 7 синих и 3 зеленых карандаша? Работая с этими задачами, необходимо сделать вывод, что в первом случае мы выбираем или один красный, или один синий, или один зеленый карандаш (правило сложения), а во втором случае - одну коробку конфет и одну коробку печенья (правило умножения). Этот опыт потребуется ученикам при решении задач на вычисление вероятности сложных событий. Комбинации с повторениями возможно рассмотреть на внеклассных занятиях по математике. Изучение комбинаторики важно и продиктовано самой жизнью. Классы задач, решаемые комбинаторными методами, очень многообразны. Для развития логики рассуждений, интуиции, мышления и многого другого, человеку для начала следует ознакомиться со способами решения основных задач. Обучение комбинаторике нужно начинать с решения легких комбинаторных задач методом непосредственного перебора. Операция перебора, служит основой для формирования комбинаторных понятий и хорошей подготовкой к выводу комбинаторных формул и закономерностей и раскрывает идею комбинирования. После того как ученики научаться создавать наборы из элементов заданного множества по заданному свойству, на первый план выходит задача по подсчету количества возможных наборов. Такие комбинаторные задачи решаются с помощью рассуждений, раскрывая принцип умножения. Оптимальной визуальной иллюстрацией правила умножения является дерево возможных вариантов. Важно показать его использование при решении комбинаторных задач. 14.Методика изучения элементов теории вероятностей в школе. 15.Методика изучения элементов статистики в школе. 16.Различные трактовки понятия функции. Функциональная пропедевтика в 5-6 классах  | ||||||||