Лекция 17. Методика изучения важнейших величин

• Название: Методика изучения важнейших величин
• Дата: 02.03.2023
• Размер: 0.68 Mb.
• Имя файла: Лекция 17.docx
• Тип: Лекция; #964369

Лекция 17

МЕТОДИКА ИЗУЧЕНИЯ ВАЖНЕЙШИХ ВЕЛИЧИН
Методика ознакомления с длиной отрезка и с единицами измерения длины

В начальных классах рассматриваются величины: длина, площадь, масса, емкость, время и другие. Уча­щиеся должны получить конкретные представления об этих величинах, ознакомиться с единицами их измере­ния, овладеть умениями измерять величины, научить­ся выражать результаты измерения в различных еди­ницах, выполнять арифметические действия над име­нованными числами.

Каждая изучаемая величина — это некоторое обоб­щенное свойство реальных объектов окружающего мира. Упражнения в измерениях развивают простран­ственные представления, вооружают учащихся важны­ми практическими навыками, которые широко приме­няются в жизни. Следовательно, изучение величин — это одно из средств связи обучения с жизнью.

Величины рассматриваются с 1 по 4 класс в тесной связи с изучением целых неотрицательных чисел и дро­бей: обучение измерению связывается с обучением сче­ту; новые единицы измерения вводятся вслед за введе­нием соответствующих счетных единиц; образование, запись и чтение именованных чисел изучается парал­лельно с нумерацией отвлеченных чисел; арифметичес­кие действия выполняются над отвлеченными и над именованными числами. Измерительные и графические работы как наглядное средство используются при ре­шении задач. Таким образом, изучение величин способ­ствует усвоению многих вопросов курса математики.

Первые представления о длине как свойстве предме­тов у детей возникают задолго до школы. К началу обу­чения в школе дети выделяют без ошибок линейную протяженность (длина, ширина, высота предметов, рас­стояние между ними). Они правильно устанавливают отношения: длиннее — короче, шире — уже, дальше — ближе и т.п., если различия в этом плане ярко выра­жены, а по другим свойствам предметы сходны.

Важным шагом в формировании понятия о линей­ной протяженности является знакомство с прямой ли­нией и отрезком как «носителем» линейной протя­женности, лишенным по существу других свойств. Сравнивая отрезки на глаз, дети получают представ­ление о равных и неравных отрезках.

На следующем этапе происходит знакомство с пер­вой единицей измерения отрезков — сантиметром. Для этого можно использовать мультфильм «38 попугаев» или предложить детям различные упражнения на срав­нение длины предметов на глаз, где невозможно нало­жить один предмет на другой. В этом случае подводим детей к выводу, что нужно выбрать единицу измере­ния (такой единицей может быть, например, шаг)

В результате выполнения практической работы дети сами приходят к выводу о том, что результат измере­ния длины может меняться в зависимости от выбран­ной единицы измерения (например, от длины шага). В связи с этим удобно выбрать постоянную единицу длины.

Чтобы дети получили наглядное представление о сантиметре, следует выполнить ряд упражнений. На­пример, дать задание, чтобы они сами изготовили модели сантиметра, начертили отрезки длиной 1 см в тетрадях (по клеточкам), нашли, что ширина ми­зинца примерно равна 1 см.

Далее учащихся знакомят с измерением отрезков. Чтобы дети ясно поняли процесс измерения и что по­казывают числа, получаемые при измерении, целесо­образно постепенно переходить от простейшего приема укладывания моделей сантиметра и их подсчета к бо­лее трудному — отмериванию. Только затем присту­пить к измерению способом прикладывания линейки. При работе с масштабной линейкой обращается вни­мание на правильность положения линейки при изме­рении. Следует научить детей выполнять округление результатов измерения.

Для формирования измерительных навыков вклю­чается система разнообразных упражнений. Это изме­рение и черчение отрезков; сравнение отрезков. Чтобы ответить на вопрос: на сколько сантиметров длиннее (короче) один отрезок от другого; увеличение и умень­шение их длины на несколько сантиметров.

Позднее, при изучении нумерации чисел в пределах 100, вводятся новые единицы измерения — дециметр, метр. Работа ведется аналогично той, что и при зна­комстве с сантиметром. Затем устанавливают отноше­ния между единицами измерения. Дети упражняются в измерении с помощью двух разных мерок и получа­ют в результате составные именованные числа (напри­мер, длина крышки стола 4 дм 5 см и т.д.). С этого времени приступают к сравнению именованных чисел на основе сравнения соответствующих отрезков.

Затем рассматривают преобразования именованных чисел — замену крупных единиц мелкими (3 дм 5 см = 35 см) и мелких единиц крупными (48 см = 4 дм 8 см).

Далее знакомство с единицами измерения длины продолжается: дети знакомятся с миллиметром, а позд­нее с километром.

Введение миллиметра обосновывается необходимос­тью измерять отрезки, меньше 1 см. Наглядное пред­ставление 6 миллиметре дети получают, рассматривая деления на обычной масштабной линейке или на мил­лиметровой бумаге. Сразу же устанавливается, сколь­ко миллиметров содержится в 1 см, и дети приступают к измерениям с точностью до миллиметра. Обращает­ся внимание на то, что на линейке сантиметры обозна­чены длинными черточками, а миллиметры — корот­кими, но каждые 5 мм обозначены более длинными черточками, что облегчает измерение.

При знакомстве с километром полезно провести прак­тические работы на местности, чтобы сформировать представление об этой единице измерения. Можно со­вершить экскурсию на улицу, пройти 1 км. Затем учи­тель дает задание учащимся составить таблицу рассто­яний между отдельными поселками. Потом этот мате­риал используется на уроках при составлении задач.

При изучении единиц длины основной единицей изме­рения является метр (1 м). Все остальные единицы про­изводные от метра: сантиметр составляет сотую долю метра (приставка санти означает сотая), дециметр — де­сятую долю метра, миллиметр — тысячную долю метра.

При изучении каждой новой единицы измерения длины дается соотношение и к концу изучения мер длины составляется и заучивается наизусть таблица:

1 м = 10 дм = 100 см

1 дм = 10 см = 100 мм

1 см - 10 мм

1 км = 1000 м

Методика ознакомления с массой и с единицами измерения массы

При изучении единиц массы можно придерживать­ся того же подхода: опираясь на те конкретные пред­ставления, которые есть у детей, обобщить и система­тизировать их в ходе проведения практических работ. При этом этапы формирования представлений анало­гичны тем, которые использовались при измерении длины: сравнение массы предметов по ощущению (тя­желее, легче на руке), выяснение отношения «тяже­лее», «легче» с помощью инструмента — чашечных весов, а затем уже отвешивание и взвешивание груза с помощью весов и гирь (разновесов), когда выбрана еди­ница измерения массы. Дети знакомятся сначала с ки­лограммом, затем с граммом.

При знакомстве с единицами измерения массы мож­но провести экскурсию, где детям удастся познакомиться с различными видами весов, запомнить массу некото­рых предметов (буханка хлеба, число яблок в кило­граммах и т.д.)- При этом важно научить детей учи­тывать тару при взвешивании. Если состав класса до­статочно сильный, можно познакомить с имеющими практическое значение понятиями «вес нетто» (вес гру­за без тары), «вес брутто» (вес груза вместе с тарой).

В 4 классе дети знакомятся с более крупными еди­ницами измерения массы: центнером и тонной — и по­лучают конкретные представления о том, какие пред­меты могут иметь ту или иную массу, знакомятся с соотношениями 1 ц = 100 кг, 1 т = 1000 кг, решают вопрос о том, массу каких предметов удобнее измерять в тех или иных единицах.

Новые единицы массы включаются в систему знаний об измерении величин, устанавливаются соотношения новых единиц с известными ранее. И, наконец, состав­ляется таблица единиц массы и заучивается наизусть.

После введения разных величин (длина и масса) еди­ницы длины и массы изучаются параллельно, во взаи­мосвязи друг с другом. Дети должны осознать, что еди­ницы длины и массы относятся к метрической системе мер: 1 т = 10 ц, 1 ц = 100 кг, 1 см = 10 мм и т.д. Именно это позволяет рассматривать величины в тес­ной связи с изучением нумерации.

В 4 классе изучают и преобразование именованных чисел, выраженных в единицах измерения массы, а также сравнивают составные именованные числа и выполняют арифметические действия над ними. В про­цессе этих упражнений закрепляются знания таблицы единиц массы.

Начиная со 2 класса в процессе решения простых, а затем составных задач учащиеся устанавливают и используют взаимосвязь между величинами: масса, учат­ся вычислять каждую из величин, если известны зна­чения двух других.

Формирование временных представлений у младших школьников.

Единицы измерения времени

Наиболее трудны для детей временные представле­ния. Поэтому большое значение приобретает формиро­вание конкретных представлений о каждой единице времени на основе практических работ и решения за­дач. При изучении данной величины особое значение имеет наглядность (использование календарей, моде­лей часов, секундомера, «ленты времени»).

Первые представления о времени дети получают в дошкольный период. Смена дня и ночи, смена времен года, повторяемость режимных моментов в жизни ре­бенка — все это формирует временные представления.

Временные представления у первоклассников фор­мируются, как и у дошкольников, прежде всего в про­цессе их практической (учебной) деятельности: режим дня, ведение календаря природы, восприятие последо­вательности событий при чтении сказок, рассказов, ежедневная запись в тетрадях даты работы — все это помогает ребенку увидеть изменения времени, почув­ствовать течение времени. Программа предусматрива­ет в 1 классе знакомство детей с названиями дней не­дели и их последовательностью.

Начиная с 1 класса, необходимо приступить к срав­нению знакомых, часто встречающихся в опыте детей временных промежутков. Например, что длится доль­ше: урок или перемена, учебная четверть или канику­лы, что короче по времени: занятия ученика в школе или рабочий день родителей? Такие задания способ­ствуют развитию чувства времени.

Знакомство с единицами времени способствует уточ­нению временных представлений детей. Знание коли­чественных отношений единиц измерения помогает срав­нивать и оценивать по продолжительности промежут­ки времени, выраженные в тех или иных единицах времени. Такие единицы времени, как месяц, год, сут­ки, час и минута, изучаются в 3 классе, а век и секун­да — в 4 классе. Необходимо формировать у детей кон­кретные представления о каждой единице времени, до­биваться усвоения их соотношений, научить пользо­ваться календарем и часами и с их помощью решать несложные задачи на вычисление продолжительности события, если известны его начало и конец, а также задачи, обратные данной.

Знакомя детей с месяцем и годом, учитель исполь­зует табель-календарь. По нему дети выписывают на­звания месяцев по порядку и количество дней в каж­дом месяце. Сразу же выделяют одинаковые по про­должительности месяцы, отмечают самый короткий месяц — февраль, и т.д.

Понятие о сутках раскрывается через близкие де­тям понятия о частях суток — утро, день, вечер, ночь. Кроме того, опираются на представления временной последовательности: вчера, сегодня, завтра. Дети ус­танавливают, сколько суток проходит со вчерашнего вечера до завтрашнего вечера, сколько суток прошло от начала недели до субботы, которые по счету сутки наступят, объясняют пословицу: «День и ночь — сут­ки прочь».

Следующими рассматриваются час и минута. Конк­ретные представления о соответствующих промежутках времени также формируются через практическую дея­тельность детей, через наблюдения. Чтобы ощутить вре­мя продолжительностью в 1 минуту, включают упраж­нения, с помощью которых дети узнают, что можно успеть сделать за 1 минуту. Уместно здесь объяснить смысл пословицы: «Минута час бережет».

Важным моментом на данном этапе является зна­комство с часами. Чтобы дети научились устанавли­вать время по часам, можно проводить практические упражнения, используя модель часов. Даются разные формы чтения показаний часов. С помощью модели часов решаются задачи на определение продолжитель­ности события, начала или конца его.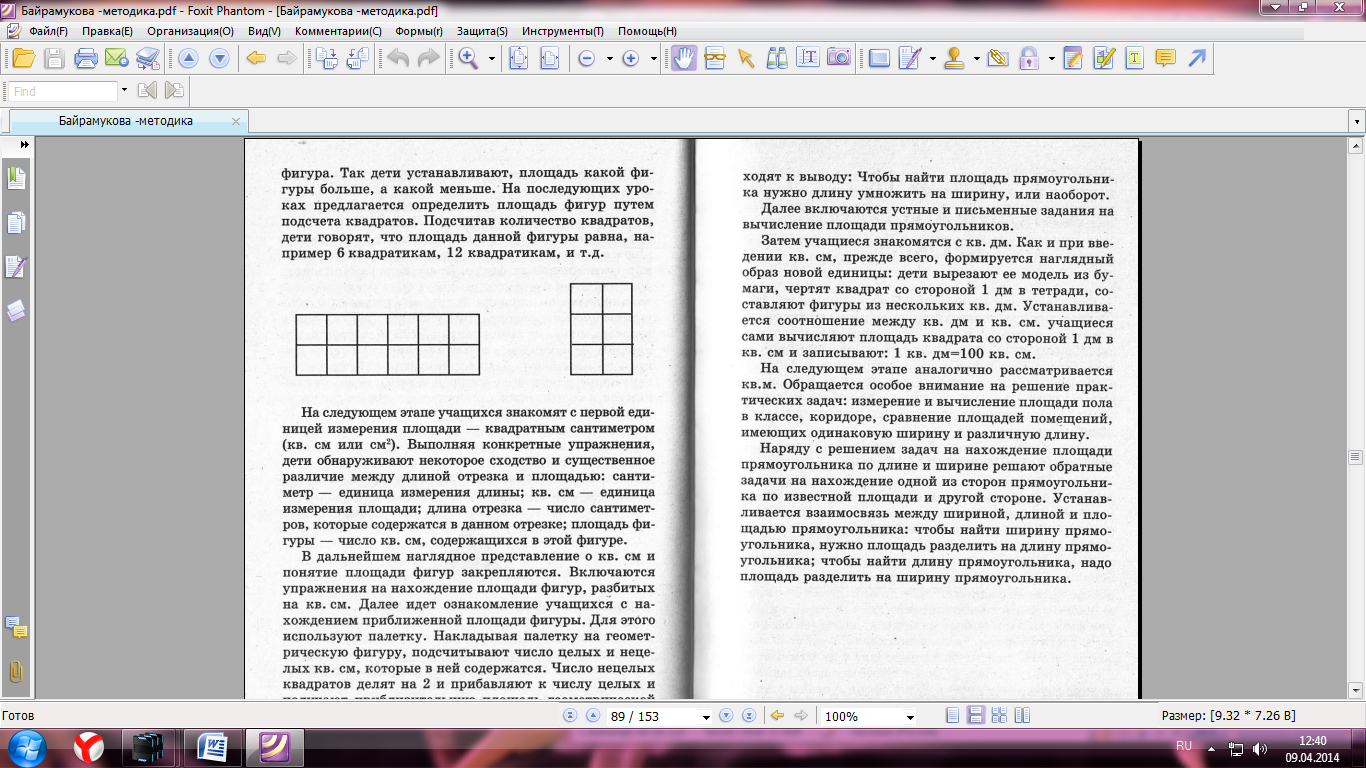

На следующем этапе учащихся знакомят с первой еди­ницей измерения площади — квадратным сантиметром (кв. см или см²). Выполняя конкретные упражнения, дети обнаруживают некоторое сходство и существенное различие между длиной отрезка и площадью: санти­метр — единица измерения длины; кв. см — единица измерения площади; длина отрезка — число сантимет­ров, которые содержатся в данном отрезке; площадь фи­гуры — число кв. ем, содержащихся в этой фигуре.

В дальнейшем наглядное представление о кв. см и понятие площади фигур закрепляются. Включаются упражнения на нахождение площади фигур, разбитых на кв. см. Далее идет ознакомление учащихся с на­хождением приближенной площади фигуры. Для этого используют палетку. Накладывая палетку на геомет­рическую фигуру, подсчитывают число целых и неце­лых кв. см, которые в ней содержатся. Число нецелых квадратов делят на 2 и прибавляют к числу целых и получают приблизительную площадь геометрической фигуры.

На следующем этапе учащиеся знакомятся с при­емом вычисления площади прямоугольника. В ходе выполнения по учебнику различных упражнений приходят к выводу: Чтобы найти площадь прямоугольни­ка нужно длину умножить на ширину, или наоборот.

Далее включаются устные и письменные задания на вычисление площади прямоугольников.

Затем учащиеся знакомятся с кв. дм. Как и при вве­дении кв. см, прежде всего, формируется наглядный образ новой единицы: дети вырезают ее модель из бу­маги, чертят квадрат со стороной 1 дм в тетради, со­ставляют фигуры из нескольких кв. дм. Устанавлива­ется соотношение между кв. дм и кв. см. учащиеся сами вычисляют площадь квадрата со стороной 1 дм в кв. см и записывают: 1 кв. дм =100 кв. см.

На следующем этапе аналогично рассматривается кв.м. Обращается особое внимание на решение прак­тических задач: измерение и вычисление площади пола в классе, коридоре, сравнение площадей помещений, имеющих одинаковую ширину и различную длину.

Наряду с решением задач на нахождение площади прямоугольника по длине и ширине решают обратные задачи на нахождение одной из сторон прямоугольни­ка по известной площади и другой стороне. Устанав­ливается взаимосвязь между шириной, длиной и пло­щадью прямоугольника: чтобы найти ширину прямо­угольника, нужно площадь разделить на длину прямо­угольника; чтобы найти длину прямоугольника, надо площадь разделить на ширину прямоугольника.

По ходу знакомства с очередной единицей времени нужно давать соотношение между единицами и заучить наизусть.

В 4 классе дети знакомятся с новыми единицами времени: секундой и веком. Сообщается, что секун­да — еще меньшая единица измерения времени, чем минута. Хорошо, если дети сами проверят, сколько шагов можно сделать за 1 с, что за 10 с можно посчи­тать от 20 до 30 и т.п.

Век — более крупная единица измерения времени, чем год (век — 100 лет). Веками измеряются длитель­ные периоды в истории стран, городов, жизнь некото­рых деревьев и животных. Данный в учебнике чертеж (шкала веков) позволяет детям находить отрезки, обо­значающие 1 век, 4 века, 20 веков и т.п. Для усвое­ния данной единицы времени полезны вопросы: какие годы находятся между черточками 19 век и 20 век? Какой сейчас год? А какой век?

Обобщением всей работы по изучению единиц изме­рения времени является составление таблицы соотно­шений между единицами времени с записью ее на клас­сной доске и в тетрадях.

1 неделя =7 дней

1 сутки = 24 часа

1 час = 60 минут

1 минута = 60 секунд

1 год =12 месяцев

1 месяц =30, 31 день — февраль=28, 29 — високос­ный год

1 век =100 лет

При изучении понятия год можно использовать сказ­ку «12 месяцев».

В связи с изучением данной темы полезно провести внеклассное занятие, на котором поставить задачу – расширить знания детей о времени и его измерении, пробудить интерес у учащихся к этому материалу. Это могут быть рассказы о том, как человек измеряя время в далеком прошлом, о первых календарях и часах, и др.

С площадью геометрической фигуры дети знакомят­ся в 4 классе.

Прежде всего, площадь выделяется как свойство плоских предметов среди других их свойств. В процес­се изучения геометрического материала у детей уточ­няются представления о площади как о свойстве плос­ких геометрических фигур. Более четким становится понимание того, что фигуры могут быть различными и одинаковыми по площади. В процессе решения задач с геометрическим содержанием учащиеся знакомятся с некоторыми свойствами площади. Они убеждаются, что площадь не изменяется при изменении положения фи­гуры на плоскости. Дети многократно наблюдают со­отношение между всей фигурой и ее частями, упраж­няются в составлении различных по форме фигур из одних и тех же заданных частей.

Ознакомление с площадью проходит так: Учитель берет треугольник и круг, накладывает одну фигуру на другую и говорит: «В этом случае говорят, что пло­щадь треугольника меньше площади круга или пло­щадь круга больше площади треугольника».



Однако не всегда так легко установить, какая из двух фигур имеет большую площадь или они одинако­вы по площади. Чтобы показать это учащимся, можно предложить им сравнить прямоугольник и квадрат, незначительно отличающиеся по площади: например: квадрат — 4·4 см, прямоугольник — 5·3 см. Снача­ла дети пытаются определить на глаз, затем способом наложения. Однако оба способа не помогают детям решить вопрос. Выслушав все ответы, учитель пово­рачивает другую сторону фигур и предлагает сосчи­тать, сколько одинаковых квадратов содержит каждая фигура. Так дети устанавливают, площадь какой фи­гуры больше, а какой меньше. На последующих уро­ках предлагается определить площадь фигур путем подсчета квадратов. Подсчитав количество квадратов, дети говорят, что площадь данной фигуры равна, на­пример 6 квадратикам, 12 квадратикам, и т.д.