Методика подготовки и проведения интегрированных. Методика подготовки и проведения интегрированных занятий по математике с другими дисциплинами. КосолаповаКалиновская Оксана Львовна, Учитель математики мбоу Гимназия 183
 Скачать 25.07 Kb. Скачать 25.07 Kb.
|
|
Методика подготовки и проведения интегрированных занятий по математике с другими дисциплинами. Косолапова-Калиновская Оксана Львовна, Учитель математики МБОУ «Гимназия №183», г. Казань Нестандартное занятие – это импровизированное учебное занятие с нетрадиционной структурой. Термин нетрадиционная форма занятия включает в себя нетрадиционные: Подготовку и проведение занятия; Структуру занятия; Взаимоотношение и распределение ролей и обязанностей между преподавателями и студентами; Подбор и критерии оценки учебных материалов; Методику оценки деятельности студентов; Анализ занятия [3:12-13]. Интеграция – это глубокое взаимопроникновение, слияние в одном учебном материале обобщенных знаний в той или иной области. Интегральные занятия дают студенту широкое представление о мире, в котором он живет, о взаимосвязи явлений и предметов о существовании мира материальной и художественной культуры. Особую значимость приобретает образное мышление. Развивают творческую активность обучающихся. Такие занятия позволяют использовать содержание всех учебных дисциплин, привлекать данные из различных областей науки, культуры, искусства. Структура интегрированных занятий. В форме интегрированных занятий целесообразно проводить – обобщающие уроки, на которых раскрываются проблемы двух или нескольких предметов. Интегрированные занятия могут вести два и более преподавателей. Педагогическая и методическая технология интегрирования занятий может быть различной, однако в любом случае необходимо их моделирование. Закономерности интегрированных занятий. Занятие подчинено авторскому замыслу. Стержень занятия – его основная мысль. Занятие – единое целое, его этапы – фрагменты целого. Этапы и компоненты занятия в логико-структурной зависимости. Дидактический материал соответствует замыслу [2:197-199]. Соблюдение указанных закономерностей означает, что занятие можно рассматривать как научно-деловое построение, в котором важны комплекс знаний и умений, свободное оперирование ими, соотношение изученного и изучаемого, соединение отдельных зачетов в одно общее, предупреждение недочетов. Анализ интегрированного занятия. Объект интеграции. Содержание и компоненты интеграции. Направление и объем интегрируемых дисциплин – в чем он выражается. Уровень интеграции содержания в курсе или занятие. Тема интегрированного занятия, проблема, цель. Деятельность преподавателя и студентов по подготовке к интегрированному занятию. Формы проведения интегрированного занятия, виды деятельности преподавателей и студентов. Сотрудничество преподавателей на интегрированном занятии. Результат деятельности студентов на интегрированном занятии. Подготовка любой нетрадиционной формы занятий требует от преподавателя больших затрат сил и времени, поскольку он обычно выступает в роли организатора. Для успешной подготовки нетрадиционного занятия и его проведения преподаватель должен обладать рядом личностных качеств и соответствовать некоторым требованиям, основными из которых являются: Хорошее знание предмета и методики; Творческий подход к работе, изобретательность; Осознанное отношение к использованию нетрадиционных форм занятий в учебном процессе. Приложение. План интегрированного занятия по дисциплинам «Математика» и «Экономика». Тема занятия: «Экономика – точная наука?!» Эпиграф занятия: «Благосостояние народа зависит от прогресса математики». (Б.Наполеон) Структура занятия. 1. Организационный момент. Основная проблема, которая должна решиться на занятие: «Зачем будущему специалисту экономики и бухгалтерского учета математические знания в объёме, определяемым Федеральным государственным образовательным стандартом специальности 080114 Экономика и бухгалтерский учет (по отраслям). Для этого надо ответить на следующие вопросы: Почему инфляция зависит от эмиссии денег? Почему повышение размера оплаты труда незамедлительно приводит к росту цен? Почему самая высокая цена не обеспечивает продавцу самых больших доходов? Нужно знать не только экономику, но и математику. 2. Актуализация знаний. - решение задач экономики с применение ранее полученных математических знаний (каждая фирма представляет презентацию по решению задачи): 1)В Лидии цены выросли на 20%. Объем продаж увеличился с 30 млр. до 33 млр. купонов. Скорость обращения не изменилась. На сколько процентов изменилось предложение денег? 2)Банк ежегодно увеличивает на одно и тоже число процентов сумму, имеющуюся на вкладе к моменту начисления процентов. На сколько процентов ежегодно увеличивается сумма, если за два года она возросла с 2000 до 2420 рублей? 3)Учителям повысили заработную плату. Доходы остальных групп населения не изменились. Количество выпускаемых холодильников после повышения заработной платы учителей не возросло. Изменилась ли средняя цена на холодильники 4)Законопослушный предприниматель закупил гвоздей по цене 3р 80коп за килограмм. Максимальная торговая наценка по законодательству равна 60%. Как показал опыт, функция спроса за данный товар может быть представлена в виде зависимости Q(P) = - P2 – P +110, где Q – объем продаж (кг за рабочий день), Р – цена (руб/кг). Какую наибольшую выручку может получить предприниматель за первый рабочий день, продавая гвозди по постоянной цене? б) тест «Проверь себя». 3. Закрепление знаний. 1) Дайте определение производной функции. 2) Вычислите производные sinx, х2, х3, 3х2, -2х3, sin1, х, ln100. 3)Сформулируйте теорему Ферма (наибольшее и наименьшее значение функции на отрезке). 4)Найдите и наименьшее значение функции у=3х2 – 6х на отрезке 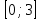 . .5)Производственные мощности позволяют предприятию «Линотрон» выпускать не более 600 тонн ваты в год. Зависимость величины совокупных издержек Сt (в тыс.рублей) от годового объёма производства Q (в тоннах) имеет вид Ct (Q) = 10Q + 1000. Связь между годовым объёмом продаж ваты, который совпадает с объёмом годового производства, и ценой на вату Р (в тыс. рублей за тонну) описывается функцией Q(Р) = - 2 Р2 - 4 Р +798. Цена на вату устанавливается 1 января 1995 года и пересматривается лишь 1 января следующего года. Найдите с точностью до 1% рентабельность производства по издержкам, если за 1995 год предприятие получит максимально возможную прибыль. (11%) 4. Подведение итогов. « В каждом знании столько истины, сколько математики!»(И.Кант). Достаточно открыть любой учебники экономики, он «нашпигован» хитрыми формулами, графиками, задачами. А потому, экономика – точная наука! Библиографический список. 1. Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям/ (Н.Ш.Кремер и др.); под ред.проф.Н.Ш.Кремера. – 3-е изд. – М.: ЮНИТИ-ДАНА, 2008. – 479 с. 2. Епишева О.Б. Общая методика преподавания математики в средней школе. Курс лекций. – Тобольск. Изд-во ТГПИ им.Д.И.Менделеева.1997.–327 с. 3. Карпушина Н. Нетрадиционная форма урока: замысел, организация, анализ. //Математика. -1998. - №9. – 12,13 С. |
