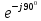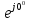курсач. Методика расчета электрических цепей постоянного тока
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
2. МЕТОДИКА РАСЧЕТА ЛИНЕЙНЫХ ОДНОФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА Электрическая схема цепи однофазного переменного тока изображена на рисунке 2.1. Исходные данные для выполнения расчета: R1 = 8 Ом; XС1= 6 Ом; XL2 = 12 Ом; R2 = 9 Ом; ХC3 = 10 Ом; U = 127 В. Необходимо: определить токи методом проводимостей; найти токи символическим методом; рассчитать мощности S, Р, Q, п  остроить топографическую векторную диаграмму токов и напряжений. остроить топографическую векторную диаграмму токов и напряжений.Рисунок 2.1 - Схема для расчета однофазной электрической цепи переменного тока 1. Расчет линейной однофазной электрической цепи переменного тока методом проводимостей Рассчитаем проводимости на параллельном участке цепи. Активные проводимости: g2= 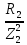 = = 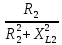 = = 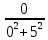 = 0; = 0;g3= 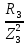 = = 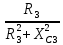 = = 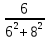 = 0,06 (См). = 0,06 (См).Реактивные проводимости: b2= 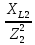 = = 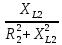 = = 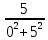 = = 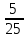 = 0,2 (См); = 0,2 (См);b3= 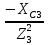 = = 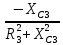 = = 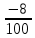 = -0,08 (См). = -0,08 (См).Полную проводимость на участке 23 определим по формуле y23 = 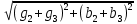 = = 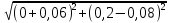 = = = 0,134164 (См). Полная проводимость ветви 23: у2 = 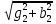 = = 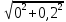 = 0,2 (См); = 0,2 (См);Полная проводимость ветви 253: у3 = 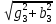 = = 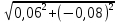 = 0,1 (См). = 0,1 (См).Рассчитаем полное сопротивление участка 23: Z23 = 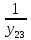 = = 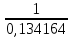 = 7,45356 (Ом). = 7,45356 (Ом).Определим активное и реактивное сопротивления параллельного участка 23: R23 = 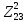 · g23= 7,453562· 0,06 = 3,33333 (Ом); · g23= 7,453562· 0,06 = 3,33333 (Ом);X23 = 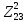 · b23= 7,453562· (0,2 – 0,08) = 6,66667 (Ом). · b23= 7,453562· (0,2 – 0,08) = 6,66667 (Ом).Сопротивление Х23 - положительное, т. е. является индуктивным. Теперь в схеме все сопротивления включены последовательно и поэтому полное сопротивление всей цепи: Z = 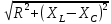 = = 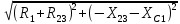 = = = 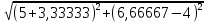 = 8,47960 (Ом). = 8,47960 (Ом).Ток в цепи определяем по закону Ома: I = I1 = 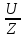 = = 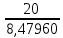 = 2,28582 (А). = 2,28582 (А).Для того чтобы найти токи I2, I3, определим напряжение на этом участке: U23= I1·Z23= 2,28582·7,45356 = 17,0375 (В). Токи I2, I3 находим по закону Ома: I1 = U23· y2 = 17,0375·0,2 = 3,4075 (A); I1 = U23· y2 = 17,0375·0,1 = 1,70375 (A). 2. Расчет линейной однофазной электрической цепи переменного тока символическим методом Символический метод расчета основан на использовании комплексных чисел. Если ток и напряжение изменяются по синусоидальному закону i= Im·sin(t+ i) и и = Um·sin(t+ u), то их также можно изобразить векторами и, следовательно, записать комплексными числами: 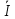 = I· = I·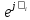 ; ;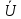 = U· = U·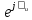 . .где 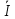 и и 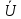 - комплексы тока и напряжения; I и U - модули комплексов тока - комплексы тока и напряжения; I и U - модули комплексов тока I = 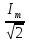 и напряжения U= и напряжения U= 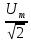 , они же действующие значения; i, u– аргументы , они же действующие значения; i, u– аргументыкомплексов токов и напряжения, они же начальные фазы тока и напряжения. Точка над величинами указывает, что ток и напряжение изменяются по синусоидальному закону с определенной частотой . Комплекс полного сопротивления цепи 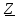 определяется отношением комплекса напряжения к комплексу тока: определяется отношением комплекса напряжения к комплексу тока: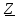 = Z = Z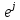 = Z·cos+ j·Z·sin, = Z·cos+ j·Z·sin,где Z - модуль комплекса полного сопротивления; - угол сдвига фаз между током и напряжением. Вещественная часть комплекса полного сопротивления есть активное сопротивление R, а коэффициент при мнимой единице j - реактивное сопротивление X: 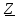 =R ± j·X. =R ± j·X.Знак перед мнимой единицей указывает на характер цепи. Знак «+» соответствует цепи индуктивного характера, а знак «-» - цепи емкостного характера (см. таблицу). Любую цепь переменного тока можно рассчитать по законам постоянного тока, если все величины представить в комплексной форме. В этом и заключается достоинство символического метода расчета. Таблица 2.1 - Полное сопротивление ветвей цепи в комплексной форме
На основании вышеизложенного рассчитаем схему, изображенную на рисунке 2.1. Н  ачертим схему замещения однофазной цепи переменного тока (рисунок 2.2). ачертим схему замещения однофазной цепи переменного тока (рисунок 2.2).Рисунок 2.2 - Схема замещения однофазной цепи переменного тока Комплексы сопротивлений участков (по номерам токов) и полного сопротивления цепи будут равны: 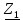 =R1 – j =R1 – j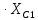 = 5 – j·4 = = 5 – j·4 = 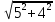 · · = 6,40312· = 6,40312·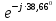 (Ом); (Ом);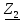 =+ j =+ j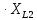 = + j·5 = 5· = + j·5 = 5·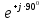 (Ом); (Ом);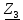 =R3 – j =R3 – j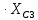 =6 – j·8 = 10· =6 – j·8 = 10·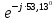 (Ом). (Ом).Комплекс сопротивления участка 23 цепи: 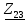 = =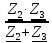 = =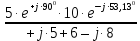 = = 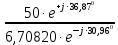 = == 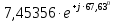 =2,81265 + j·6,90251 (Ом). =2,81265 + j·6,90251 (Ом).3. МЕТОДИКА РАСЧЕТА ТРЕХФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА 3.1. Расчет трехфазной цепи переменного тока при соединении фаз приемника звездой Для данных, приведенных в таблице 3.1, необходимо: рассчитать сопротивления элементов схемы замещения приемников; начертить схему включения приемников в трехфазную сеть; определить фазные токи каждого приемника и ток в нулевом проводе; рассчитать мощности; построить векторную диаграмму. Таблица 3.1 — Исходные данные
Линейное напряжение сети Uлин = 220 В. Выполним расчет сопротивлений элементов схемы замещения приемников: № 1: Найдем sin1. Берем со знаком « 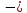 », т.к. характер нагрузки емкостной. », т.к. характер нагрузки емкостной.sin1 = 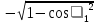 = = 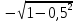 = = 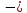 0,866025; 0,866025; Z1 = 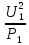 · cos 1 = · cos 1 =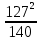 · 0,5 = 57,6036(Ом); · 0,5 = 57,6036(Ом); R1 = Z1 · cos1= 57,6036 · 0,5 = 28,8018 (Ом); X1 = Z1 · sin1 = 57,6036 · ( 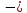 0,866025) = 0,866025) = 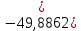 Ом); Ом);1 = arccos 0,5 = arcsin( 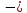 0,866025) = 0,866025) = 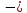 600; 600;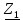 = R1 + j · X1 = Z1 · = R1 + j · X1 = Z1 · 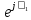 = 28,8018 = 28,8018 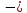 j · 49,8862 = 57,6036· j · 49,8862 = 57,6036·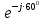 (Ом). (Ом).№ |

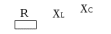 зображение на схеме
зображение на схеме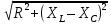 ·
·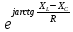 =
=
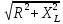 ·
·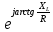 = Z·
= Z·
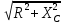 ·
·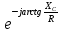 = Z·
= Z·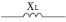
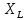 ·
·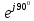
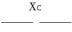
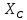 ·
·