курсач. Методика расчета электрических цепей постоянного тока
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Методика расчета электрических цепей постоянного тока Расчет простых электрических цепей постоянного тока со смешанным соединением сопротивлений методом эквивалентных преобразований Для схемы электрической цепи, изображенной на рисунке 1.1, определить токи в ветвях цепи методом эквивалентных преобразований, составить баланс мощностей. Исходные данные представлены в таблице 1.1.
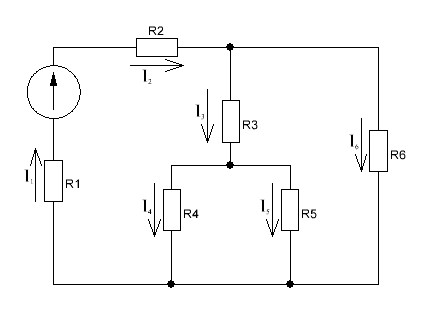 Рисунок 1.1 — Схема электрической цепи постоянного тока Расчет электрической цепи постоянного тока методом эквивалентных преобразований основан на применении свойств последовательного и параллельного соединения элементов. Свойства последовательного соединения сопротивлений: I = I1 = I2 = …; U = U1 +U2 +…; R = R1 + R2+ ... . Свойства параллельного соединения сопротивлений: I = I1 +I2 +…; U = U1 = U2 = …; 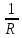 = = 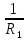 + + 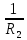 +… . +… .На схеме электрической цепи постоянного тока, представленной на рисунке 1.1, указываем направления токов в ветвях в соответствии с направлением ЭДС. Для определения токов в ветвях используем метод эквивалентных преобразований. Найдем эквивалентное сопротивление цепи относительно источника ЭДС. Рекомендуется поэтапное преобразование последовательно и параллельно соединенных сопротивлений, начиная с ветвей, наиболее удаленных от источника ЭДС. Сопротивления R4 и R5 соединены параллельно, следовательно, сопротивление R45равно: 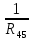 = = 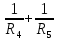 = = 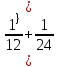 = = 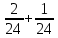 = =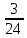 ( (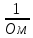 ); );R45 = 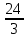 = 8 (Ом). = 8 (Ом).Свернем исходную схему (рисунок 1.1). Получаем схему цепи, изображенную на рисунке 1.2. В схеме цепи сопротивления R3 и R45 соединены последовательно, следовательно, сопротивление R345 можно рассчитать по формуле R345 = R3 + R45 = 12 + 8 = 20 (Ом). 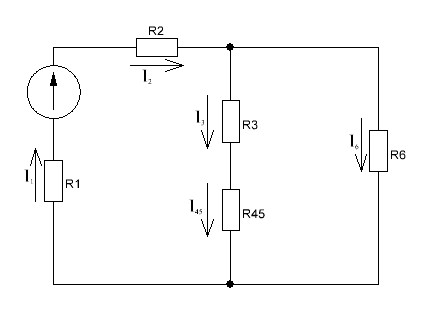 Рисунок 1.2 — Преобразованная схема электрической цепи постоянного тока Получаем схему цепи, изображенную на рисунке 1.3. В схеме цепи сопротивления R6 и R345 соединены параллельно: 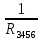 = = 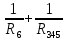 = = 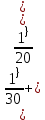 = = 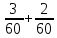 = =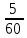 ( (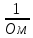 ); );R3456= 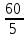 = 12 (Ом). = 12 (Ом).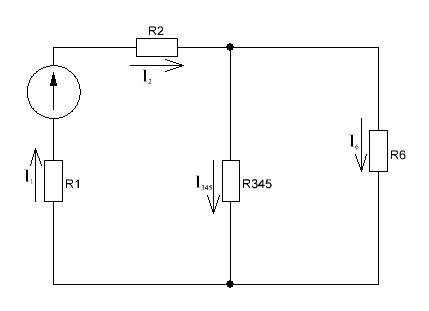 Рисунок 1.3 — Преобразованная схема электрической цепи постоянного тока Получаем схему цепи, изображенную на рисунке 1.4. В схеме цепи сопротивления R1, R2 и R3456соединены последовательно, следовательно, общее сопротивление цепи можно рассчитать по формуле R = R1 + R2 + R3456 = 10 + 5 + 12 = 27 (Ом) 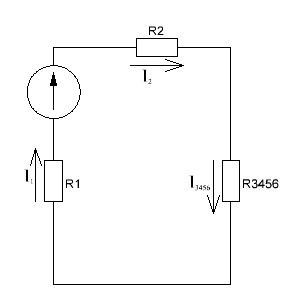 Рисунок 1.4 - Преобразованная схема электрической цепи постоянного тока Получаем схему цепи, изображенную на рисунке 1.5. 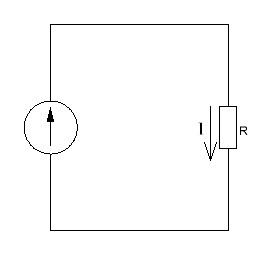 Рисунок 1.5 — Преобразованная схема электрической цепи постоянного тока Определяем токи в ветвях электрической цепи. По закону Ома для схемы цепи, изображенной на рисунке 1.5, ток I равен: I = 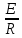 = = 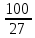 = 3,7037 (А). = 3,7037 (А).Разворачиваем схему, изображенную на рисунке 1.5, и переходим к схеме, приведенной на рисунке 1.4. I = I1 = I2 = I3456. Для определения токов в других ветвях цепи находим напряжения на этих ветвях. Напряжение U1 и U2 для схемы цепи, изображенной на рисунке 1.4, определим по закону Ома: U1 = I1 R1 = 3,7037 10 = 37,037 (В) U2 = I2 R2 = 3,7037 5 = 18,5185 (В) Напряжение U3456 для схемы цепи, изображенной на рисунке 1.4, определим по закону Ома: U3456 = I3456 R3456 = 3,7037 12 = 44,4444 (В) = U6 = U345 . По закону Ома в схеме цепи, приведенной на рисунке 1.3: I6 = 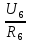 = = 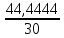 = 1,4815 (А); = 1,4815 (А);I345 = I3 =I45 = 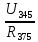 = = 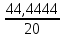 = 2,2222 (А). = 2,2222 (А).По закону Ома в схеме цепи, изображенной на рисунке 1.2: U45 = I45 R45 = 2,2222 8 = 17,7776 (В) = U4 = U5. По закону Ома в схеме цепи, приведенной на рисунке 1.1: I4 = 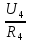 = = 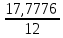 = 1,4815 (А); = 1,4815 (А);I5 = 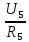 = = 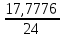 = 0,7407 (А). = 0,7407 (А).Составляем уравнение баланса мощностей: РИСТ = РПОТР. Мощность источника энергии равна: РИСТ = EI1 = 100 3,7037 = 370,37 (Вт). Мощность приемников энергии рассчитываем по формуле РПОТР = 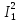 R1+ R1+ 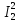 R2 + R2 + 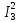 R3 + R3 + 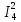 R4 + R4 + 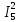 R5 + R5 + 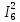 R6= R6== 3,70372 10 + 3,70372 5 + 2,22222 12 + + 1,48152 12 + 0,74072 24 + 1,48152 30 = 370,3698 (Вт); 370,37 Вт = 370,3698 Вт. Баланс мощностей соблюдается, следовательно, токи определены правильно. Методы расчета сложных электрических цепей постоянного тока Для электрической цепи, изображенной на рисунке 1.6, необходимо: определить токи во всех ветвях, используя метод узловых и контурных уравнений; рассчитать токи во всех ветвях методом контурных токов; найти токи во всех ветвях на основании метода узлового напряжения; определить токи во всех ветвях, используя метод наложения токов; составить уравнение баланса мощностей; построить потенциальную диаграмму для контура, содержащего два источника ЭДС. Параметры элементов электрической цепи указаны в таблице 1.2. Таблица 1.2 — Исходные данные
Расчет электрической цепи постоянного тока методом узловых и контурных уравнений Метод узловых и контурных уравнений подразумевает составление системы уравнений по первому и второму законам Кирхгофа. Он не требует никаких преобразований схемы и применяется для расчета любой электрической цепи. При расчете электрических цепей постоянного тока можно использовать следующий алгоритм. Произвольно задать направления действительных токов в ветвях электрической цепи. По первому закону Кирхгофа составить п - 1 узловых уравнений, где п — число узлов в цепи. Составить контурные уравнения для независимых контуров по второму закону Кирхгофа. Число контурных уравнений можно проверить по формуле т - п+1, где т — число ветвей в цепи. Составить систему уравнений из узловых и контурных уравнений. Количество уравнений в системе должно быть равно количеству ветвей (токов) в цепи. Решив данную систему, найти действительные токи. Если в результате расчета какие-либо токи получились отрицательными, это указывает на то, что их действительное направление противоположно выбранному. 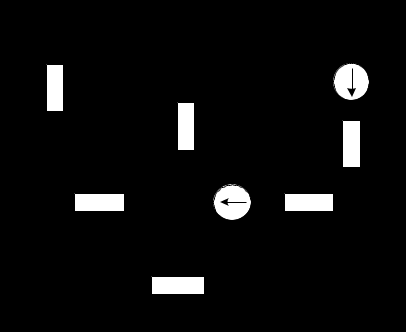 Рисунок 1.6 - Принципиальная схема электрической цепи постоянного тока Для схемы, изображенной на рисунке 1.6, указываем направления действительных токов в ветвях I1, I2, I3, I4, I5, I6. В заданной цепи шесть ветвей (т = 6), значит, в системе должно быть шесть уравнений. Сначала составляем уравнения по первому закону Кирхгофа. В цепи четыре узла (n = 4), следовательно, нужно составить три уравнения (n - 1 = 4 - 1 = 3). Например, для узлов 1, 2, 3 по первому закону Кирхгофа запишем уравнения: узел 1: –I1 + I6 – I3 = 0; узел 2: + I1 – I2 – I4 = 0; узел 3: I4 + I5 – I6 = 0. Составляем оставшиеся три уравнения по второму закону Кирхгофа для независимых контуров. Чтобы контур был независимым, необходимо в каждый следующий контур включить одну ветвь, не входящую в предыдущие. Выбираем направления обходов и составляем уравнения. При составлении уравнений учитываем следующее. Если направление ЭДС совпадает с направлением обхода контура, ЭДС записывается со знаком «+», если их направления противоположны, то ЭДС берем со знаком «–». Падение напряжения на резисторе записываем со знаком «+», если направления обхода контура и тока, протекающего через него, совпадают, а со знаком «–» - если их направления противоположны. Контур 1421 (обход против часовой стрелке): E1 = I2 R2 + I1 (R1 + R01) – I3 R3. Контур 2432 (обход по часовой стрелке): 0 = I2 R2 + I5 R5 – I4 R4. Контур 1431 (обход против часовой стрелки): E2 = I3 R3 + I6 (R6+ R02)+ I5 R5. Записываем уравнения для узлов и контуров в систему. Получили систему из шести уравнений с шестью неизвестными: 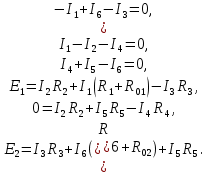 Подставляем в уравнения численные значения ЭДС и сопротивлений из таблицы 1.2: 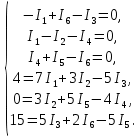 Решаем систему уравнений методом Крамера, применяя специализированные инструменты математического анализа. Заполним таблицу 1.3. Таблица 1.3 — Коэффициенты при токах из системы уравнений
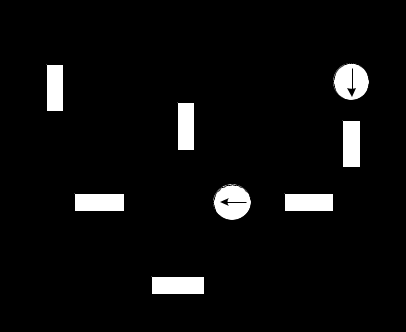 Рисунок 1.7 - Принципиальная схема электрической цепи постоянного тока Расчет электрической цепи постоянного тока методом контурных токов Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе. Достигается это разделением схемы на независимые контуры и введением для каждого контура своего контурного тока, являющегося расчетной величиной. При решении задачи данным методом можно использовать следующий алгоритм. Определить независимые контуры и выбрать в них направления контурных токов. Составить систему уравнений (количество уравнений равно количеству независимых контуров). Уравнения составить по правилу: одна сторона от знака равенства представляет собой алгебраическую сумму ЭДС, входящих в контур. По другую сторону от знака равенства стоит алгебраическая сумма из нескольких слагаемых. Первое слагаемое — это падение напряжения в данном контуре, созданное данным контурным током (произведение контурного тока и суммы всех сопротивлений, входящих в данный контур). Следующее слагаемое — это падение напряжения в данном контуре, созданное контурными токами смежных контуров (произведение смежного контурного тока на общее сопротивление двух контуров). Оно положительное, если контурные токи протекают через общий резистор в одном направлении, или отрицательное, если в разных. Решив систему, найти контурные токи. Действительный ток в смежных ветвях определить как алгебраическую сумму контурных токов, протекающих через данную ветвь. Если направления контурных токов совпадают, то действительный ток определяют как сумму токов по величине и по направлению он с ними совпадает. Если Если направления контурных токов противоположны, то действительный ток определяют как разность токов по величине и по направлению он совпадает с большим по величине током. На основании приведенного алгоритма рассчитаем схему, изображенную на рисунке 1.8. 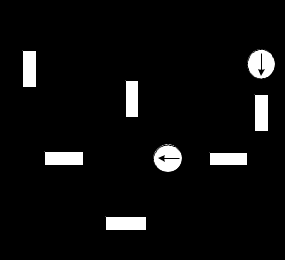 Рисунок 1.8 - Принципиальная схема электрической цепи постоянного тока Число уравнений в системе должно быть равно числу независимых контуров. В заданной цепи рассмотрим три независимых контура (1421, 2342, 1431) и введем для них контурные токи I11, I22, I33. Стрелками указываем выбранные направления контурных токов. Составляем уравнения для каждого контура. Контур 1421: E1= R1 · I11 + R2 ·(I11 + I33) +R3 · (I11 - I22). Контур 2342: 0 = R4 · I33 + R2 ·(I11 + I33) +R5 · (I22+I33). Контур 1431: E2 = R · I22 +R5 · (I22+I33)+ R3 ·(I22 – I11). Составляем систему уравнений: 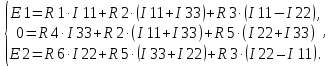 Подставляем в уравнения численные значения ЭДС и сопротивлений из таблицы 1.2: 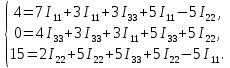 Упростим и запишем данную систему так, чтобы контурные токи во всех уравнениях располагались по порядку: 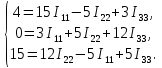 Вычислим контурные токи: I11 = 1,3048 А; I22 = 2,3349 А; I33 = -1,2991 А. Расчет электрической цепи постоянного тока методом узлового напряжения Данный метод применим к цепям с двумя узлами. Если в схеме узлов больше двух, то ее необходимо преобразовать к двум. Алгоритм расчета данным методом следующий. Преобразовать схему к двум узлам. Выбрать направление токов в ветвях к одному узлу. Рассчитать проводимость каждой ветви по формуле g = 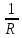 . .Определить узловое напряжение. Величину узлового напряжения определяют отношением алгебраической суммы произведения ЭДС и проводимости ветвей к сумме проводимостей всех ветвей. ЭДС источника, работающего в режиме генератора, берется со знаком «+», а источника, работающего в режиме потребителя, — со знаком «—». Uузл = 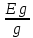 . .Определить действительные токи в ветвях по формуле I = ( ± E – Uузл) g. Приведем схему, изображенную на рисунке 2.6, к двум узлам, преобразовывая треугольник сопротивлений R1, R4, R6 в эквивалентную звезду сопротивлений R14, R46, R16. Новый узел обозначим А (рисунки 2.10, 2.11, 2.12). 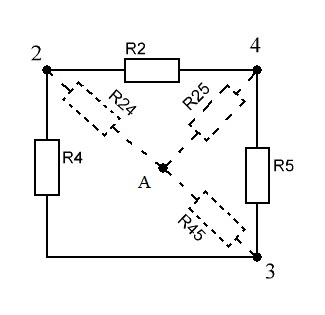 Рисунок 1.9 – Преобразование треугольника сопротивлений в звезду 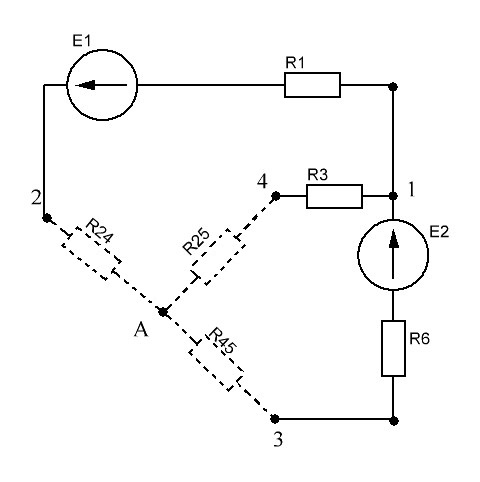 Рисунок 1.10 – Схема, преобразованная к двум узлам 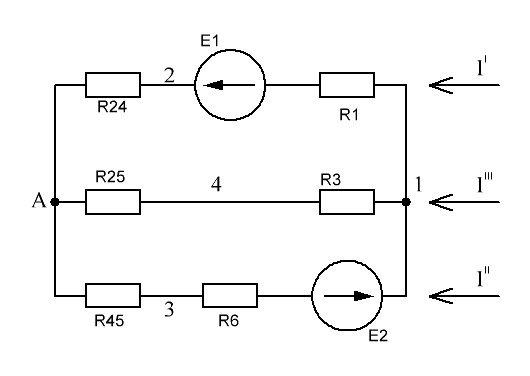 Рисунок 1.11 – Схема, преобразованная к двум узлам Рассчитаем величины сопротивлений эквивалентной звезды: R24 = 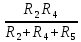 = = 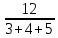 = = 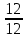 = 1 (Ом); = 1 (Ом);R16 = 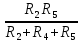 = = 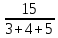 = = 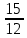 = 1,25 (Ом); = 1,25 (Ом);R45 = 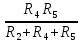 = = 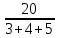 = = 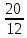 = 1,6667 (Ом). = 1,6667 (Ом).Выбираем направление токов в параллельных ветвях влево: I', I", I"'. Определим общее сопротивление каждой ветви: R' = R1+ R01 + R24 = 7 + 0 + 1 = 8 (Ом); R" = R6+ R02 + R45 = 2 + 0 + 1,6667 = 3,6667 (Ом); R'" = R3 + R25 = 5 + 1,25 = 6,25 (Ом). Рассчитаем проводимость каждой ветви: g' = 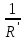 = = 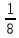 = 0,125 (См); = 0,125 (См);g'' = 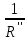 = = 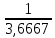 = 0,2727248 (См); = 0,2727248 (См);g''' = 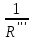 = = 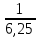 = 0,16 (См). = 0,16 (См).Определим узловое напряжение: UА1 = 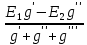 = = 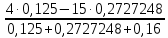 = = 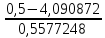 = – 6,438430 (В). = – 6,438430 (В).Находим токи в каждой ветви: I' =(E1 – UА1)·g' = (4 + 6,438430) · 0,125 = 10,43843 · 0,125 = 1,3048 (А); I'' =(-E2 – UА1)·g''= (-15 + 6,438430) · 0,2727248 = −8,56157 · 0,2727248= = −2,3349 (А); I''' =(– UА1)·g'''= 6,438430 · 0,16 = 1,0301 (А). Действительные токи равны: I1 = I' = 1,3048 А - влево; I5 = I" = −2,3349 А - вправо; I3 = I''' = 1,0301 А - влево. 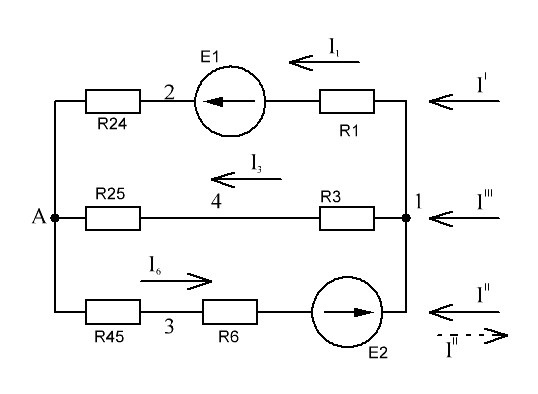 Рисунок 1.12 – Токи в каждой ветви Вернемся к исходной схеме. Выберем I6 вниз, I1и I3 влево. 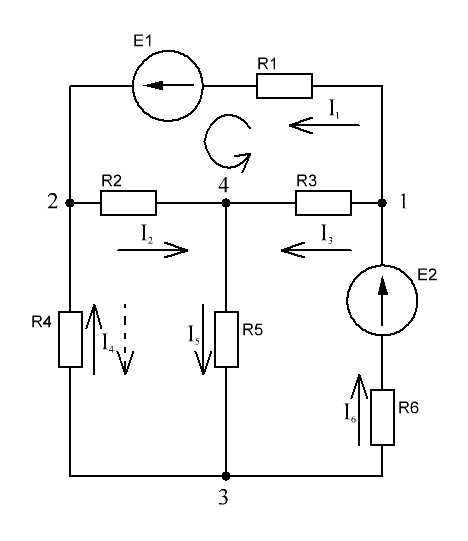 Рисунок 1.13 – Принципиальная схема электрической цепи постоянного тока Для контура 2412 составляем уравнение по второму закону Кирхгофа (обход против часовой стрелки): E1 = I1 (R1 + R01) + I2 R2 – I3 R3. Выражаем из него ток I2: I2 = 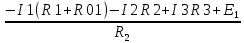 = = 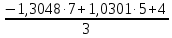 = 0,0056 (А) - вправо. = 0,0056 (А) - вправо.По первому закону Кирхгофа находим токи I4и I5: узел 4: I2 +I3 – I5 = 0; I5 = I2 + I3 = 0,0056 + 1,0301 = 1,0357 (А) - вниз; узел 2: I4 + I1 – I2 = 0; I4 = – I1 + I2= – 1,3048 +0,0056 = – 1,2992 (А) - вниз. В результате действительные токи равны: I1 = 1,3048 А; I2 = 0,0056 А; I3 = 1,0301 А; I4 = 1,2992 А; I5 = 1,0357 А; I6 = 2,3349 А. 4. Расчет электрической цепи постоянного тока методом наложения токов Метод наложения токов является одним из методов расчета сложных цепей с несколькими источниками. При решении данным методом используют следующий алгоритм решения. Составить расчетные схемы. Схемы содержат только одну ЭДС, остальные заменяют на их внутреннее сопротивление. Количество расчетных схем равно количеству источников в схеме. В каждой расчетной схеме указать направления частичных токов. Частичным называется условный ток, протекающий в ветви под действием только одного источника. Направление частичных токов в ветвях зависит от полярности источника. Используя метод преобразования схем, определить частичные токи в каждой расчетной схеме. Действительные токи найти как алгебраическую сумму частичных токов. При этом направление тока совпадает с большим по величине частичным током. Приведем исходную схему (рисунок 1.6) к двум узлам (рисунок 1.11), преобразовывая треугольник сопротивлений R2, R4, R5 в эквивалентную звезду сопротивлений R25, R45, R24. Сопротивления эквивалентной звезды рассчитаны ранее: R24 = 1 Ом; R22 = 1,25 Ом; R45= 1,6667 Ом.  Рисунок 1.11 — Схема электрической цепи, приведенная к двум узлам Для схемы электрической цепи, изображенной на рисунке 1.11, составляем расчетные схемы (рисунки 1.14, 1.15). Указываем на них направления частичных токов. Решаем первую расчетную схему (рисунок 2.17) методом эквивалентных преобразований (методом «свертывания»). 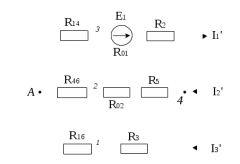 Рисунок 1.14 — Первая расчетная схема Находим общее сопротивление для первой расчетной схемы: R45,6,25,02,3 = 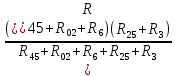 = = 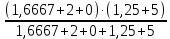 = = 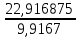 = = = 2,3109 (Ом); R' = R1 +R24 + R45,6,25,02,3 = 7 + 1 + 2,3109 = 10,3109 (Ом). Находим общий ток для первой расчетной схемы: 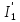 = = 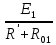 = = 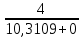 = 0,3879 (А). = 0,3879 (А). 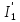 = = 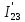 . .Рассчитываем напряжение параллельных ветвей: 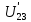 = = 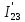 ·R45,6,25,02,3= 0,3879·2,3109 = 0,8964 (В). ·R45,6,25,02,3= 0,3879·2,3109 = 0,8964 (В).Определяем частичные токи на параллельных ветвях для первой расчетной схемы: 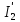 = = 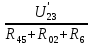 = = 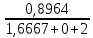 = 0,2445 (А); = 0,2445 (А);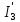 = = 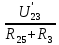 = = 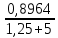 = 0,1434 (А). = 0,1434 (А).Решаем вторую расчетную схему (рисунок 2.18). Рассчитываем общее сопротивление для второй расчетной схемы: R24,01,1,25,3 = 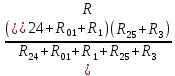 = = 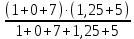 = = 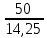 = == 3,5088 (Ом); R'' = R6+R45 + R24,01,1,25,3= 1,6667 + 2 + 3,5088 = 7,1755 (Ом). Находим общий ток для второй расчетной схемы: 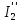 = = 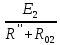 = = 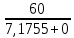 = 2,0904 (А). = 2,0904 (А). 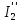 = = 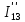 . .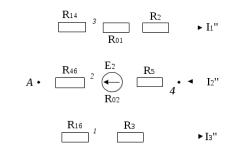 Рисунок 1.15 — Вторая расчетная схема Действительные токи находим как алгебраическую сумму частичных: I6 = 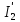 + + 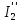 = 2,0904 + 0,2445 = 2,3349 (А) – вправо. = 2,0904 + 0,2445 = 2,3349 (А) – вправо. |
