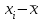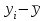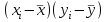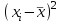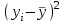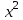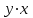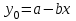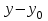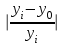Патентное исследование. Методология научных исследований и планирование эксперимента
 Скачать 222.3 Kb.
|
|
М  ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное бюджетное образовательное учреждение высшего образования «МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ)» Конструкторско-механический факультет Кафедра "Транспортные установки" ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ на тему: " Корреляционно-регрессионный анализ экспериментальных данных" Специальность: 15.03.02 «Транспортные средства специального назначения» Специализация: «Гидравлические машины, гидроприводы и гидропневмоавтоматика» Дисциплина: «Методология научных исследований и планирование эксперимента» Выполнил: студент группы 4бГП ________________ С.З. Риза-Заде Проверил: Ассистент кафедры ________________С.А. Ерусланкин Цель работы: Закрепить знания и сформировать умение проводить корреляционно-регрессионный анализ экспериментальных данных. Понятия корреляционного и регрессионного анализа экспериментальные данные: Корреляционный анализ – статистический метод оценки формы, знака и тесноты связи исследуемых признаков или факторов. Совместную изменчивость разных признаков называют «корреляция» (co-relation – связь, соотношение). В задачу статистического анализа входят выявление величины корреляционной связи и установление ее типа. Один из основных коэффициентов, измеряющих связь между варьирующими признаками х и у, является коэффициент корреляции r, который находятся в пределах от 0 до ± 1. 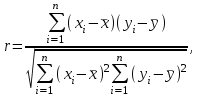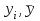Коэффициент корреляции определяется по следующему выражению:  х (1)где  – значение единичного результата и средняя арифметическая одного признака;  – значение единичного результата и средняя арифметическая другого зависимого признака.Регрессионный анализ – статистический метод исследования зависимости между зависимой переменной у и одной или несколькими независимыми переменными х1, х2,..., хn. При полном факторном эксперименте влияние факторов на результат эксперимента раскрывается с помощью уравнения регрессии. Регрессия - величина, выражающая зависимость среднего значения случайной величины у от значений случайной величины х. Уравнение регрессии выражает среднюю величину одного признака как функцию другого. Построение уравнение регрессии осуществляется в два этапа: – определение вида аналитической зависимости y=f(x); – оценка параметров выбранной модели. Для определении вида аналитической зависимости применяются три основных метода: – графический (на основе анализа поля корреляций); – аналитический, т. е. исходя из теории изучаемой взаимосвязи; – экспериментальный, т.е. путем сравнения величины остаточной дисперсии или средней ошибки аппроксимации, рассчитанных для различных моделей регрессии (метод перебора). Исходные данные: Номер мой зачетки – 170736.
Выполнение: 3.2.2. Определяем средние значения х и у.   3.2.3. Пошагово находим коэффициент корреляции. Для удобства расчет составляющих формулы (1) выполним с использованием таблицы 6. Таблица 6 Пошаговый расчет коэффициента корреляции
Рассчитываем коэффициент корреляции 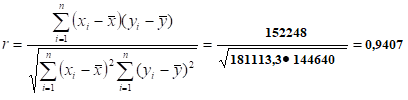 Полученное значение коэффициента корреляции показывает, что сила связи параметров х и у сильная, а характер связи – обратный. 3.2.4. Используя формулу, определяем значения коэффициентов для линейной аналитической зависимости. Для удобства выполнения расчетов подготовим данные (таблица 7). Таблица 7 Подготовка исходных данных для расчета коэффициентов уравнения регрессии
Подставляем полученные исходные данные в систему уравнений. 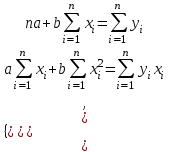 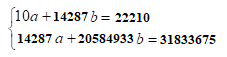 Выражаем из первого уравнения системы коэффициент a   Полученное выражение подставляем во второе уравнение системы и находим значение коэффициента b.   Определяем величину коэффициента а.  Подставляем полученные значения коэффициентов в уравнение регрессии.  3.2.5. Строим корреляционное поле экспериментальных данных и теоретическую линию, полученную по уравнению регрессии (рис. 2). 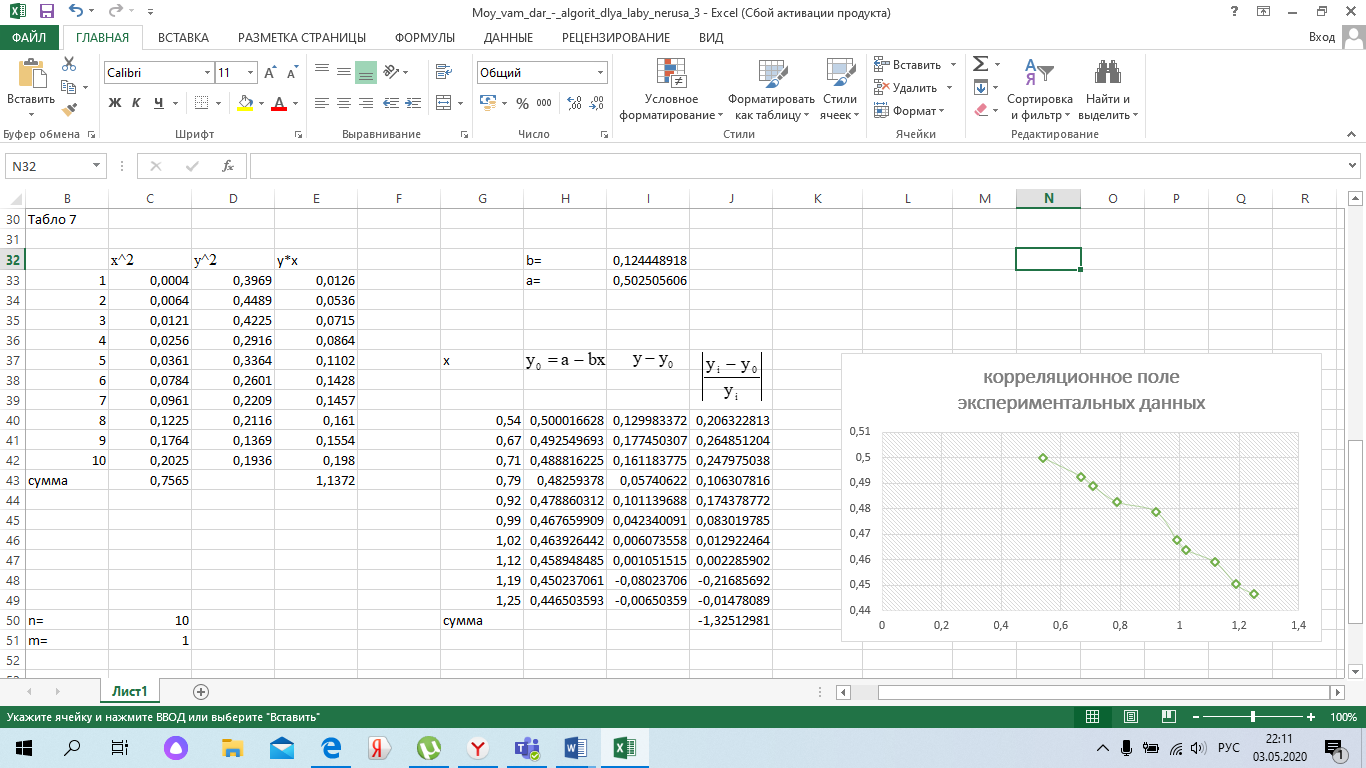 Рис. 2. Зависимость параметра у от параметра х 3.2.6. Определяем среднюю ошибку аппроксимации. Расчет произведем пошагово с использованием таблицы 8. Таблица 8 Расчет средней ошибки аппроксимации
Рассчитываем среднюю ошибку аппроксимации 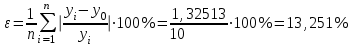 Точность аппроксимации уравнения регрессии удовлетворительна, так как ее средняя ошибка не превышает 10 %. 3.2.7. Определяем фактическое значение F-критерия Фишера 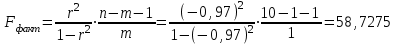 3.2.8. Определяем число степеней свободы 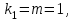 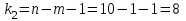 По таблице П3 приложения определяем максимально возможное значение критерия 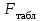 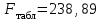 Вывод: Fфакт ˂ Fтабл, - гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии. Нет основания отклонять нулевую гипотезу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
