(код 24960) Математика. Мы помогаем учащимся со всей России!
 Скачать 160.5 Kb. Скачать 160.5 Kb.
|
 Мы помогаем учащимся со всей России! Федеральная сеть центров помощи в обучении
Аксиоматическое построение системы натуральных чисел 1. Примените законы операций и вычислите результат; каждый случай использования законов объясните: а) 7091 + (1819 + 509); ассоциативность сложения. б) (9073 + 1329) + 2671; ассоциативность сложения. в) 386 + 287 + 213 + 564; ассоциативность сложения. г) 3057 + 1561 + 1513 + 829 + 2564; ассоциативность сложения. д) (372 4) 5; ассоциативность умножения. е) 125 15 6 8; коммутативность и ассоциативность умножения. ж) 20 811 4; коммутативность и ассоциативность умножения. з) 350 44 20 50. коммутативность, дистрибутивность и ассоциативность умножения. и) 57 247 + 57 362; коммутативность, дистрибутивность и ассоциативность сложения, вычитание суммы чисел от числа. к) 37 42 + 37 36 - 78 27; – дистрибутивность сложения. л) 47 3 + 53 3; м) 5(12+25). 2. Обладает ли операция деления на множестве натуральных чисел свойством коммутативности? Свойством ассоциативности? Ответ обоснуйте. Операция деления на множестве натуральных чисел не обладает свойствами коммутативности и ассоциативности, т.к. результат действий деления зависит от порядка расположения чисел, например: Определение целого неотрицательного числа 1. Используя три подхода к определению целого неотрицательного числа, действий над числами и отношения «меньше», объясните: 3<6 0+4=4 3+2=5 5-2=3 8.2=16 12:6=2 а) Если множество А равномощно собственному подмножеству множества В и n(А) = a, n(В) = b, говорят, что число а меньше числа b, и пишут a < b: 3<6 б) Сложением целых неотрицательных чисел а и b называется бинарная алгебраическая операция, в результате которой получается целое неотрицательное число с, равное числу элементов в объединении множеств А и В: 0+4=4 3+2=5 в) Вычитанием целых неотрицательных чисел а и b называется частичная бинарная алгебраическая операция, в результате которой получается целое неотрицательное число: 5-2=3 г) Умножением целых неотрицательных чисел а и b называется бинарная алгебраическая операция, в результате которой получается целое неотрицательное число: 8.2=16 д) Пусть имеется множество А такое, что т(А) = а, и множество А разбивается на некоторое число равночисленных попарно непересекающихся подмножеств, в каждом из которых содержится по b элементов. Тогда частным с натуральных чисел а и b является число подмножеств такого разбиения, а – делимое, b – делитель, с – частное: 12:6=2 2. Обоснуйте выбор действия при решении следующих задач: а) В зоопарке 6 медведей, а верблюдов на 2 меньше. Сколько верблюдов в зоопарке? Пусть А – множество медведей, В – множество верблюдов. Мощности: n(A)=6 n(В) нужно найти По условию задачи в множестве А можно выделить подмножество С, численность которого равна 2, т.е. n(C)=2. Тогда разность множеств: А \ С = В Задача решается действием вычитания мощностей множеств: n(B) = n(А \ С) = n(А) – n(C) = 6–2 = 4 б) На каждое детское пальто нужно пришить четыре пуговицы. Сколько пуговиц нужно пришить на 7 таких пальто? Произведение двух натуральных чисел 7 и 4 – это сумма 7-ти слагаемых, каждое из которых равно 4: в) 10 тетрадей раздали 5 ученикам поровну. Сколько тетрадей получил каждый? Деление на равные части – это действие, которое связано с разъединением данного множества численностью 10 на 5 равных множеств, каждое из которых содержащих число элементов: г) В портфель положили 4 тетради в клетку и 3 тетради в линейку. Сколько тетрадей положили в портфель? Сумма двух целых положительных чисел, определяющих количества складываемых предметов, дает общее количество этих предметов: д) В одной коробке - 12 карандашей, а в другой - 9. На сколько карандашей в первой коробке больше, чем во второй? Пусть А – множество карандашей в 1-ой коробке, В – множество карандашей в 1-ой коробке. Мощности: n(A)=12 n(В)=9 По условию задачи в множестве А нужно выделить такое подмножество С, которое будет являться дополнением множества В до множества А: А \ В = С Задача решается действием вычитания мощностей множеств: n(С) = n(А \ В) = n(А) – n(В) = 12–9 = 3 е) 15 карандашей раздали ученикам по 3 карандаша. Сколько учеников получили карандаши? Деление на равные части – это действие, которое связано с разъединением данного множества численностью 15 на количество равных множеств, содержащих 3 элемента каждый: ж) В саду росло 3 дуба, а лип в 2 раза больше. Сколько лип росло в саду? Пусть А – множество дубов, В – множество лип. Мощности: n(A)=3 n(В) нужно найти По условию задачи нужно найти такое множество В, которое будет включать в себя два множества А: Задача решается действием сложения мощностей множеств: 3. Обоснуйте выбор действия при решении следующих задач: а) Купили 5 кг яблок и 4 кг груш. Сколько килограммов фруктов купили? Используем величинный подход. Масса – величина непрерывная. Длина отрезка а=5 ед. изм. показывает массу яблок, длина отрезка b=4 ед. изм. показывает массу груш, длина отрезка с показывает суммарную массу фруктов:  Неизвестная масса: с=а +b=5+4=9 ед. изм. (килограммов) б) Было 23 метра ткани. От куска ткани отрезали 6 метров. Сколько метров ткани осталось? Используем величинный подход. Длина – величина непрерывная. Длина отрезка а=23 ед. изм. показывает исходную длину, длина отрезка b=6 ед. изм. показывает отрезанную длину, отрезок с показывает остаток длины: 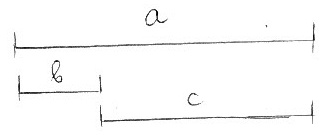 Неизвестная длина: с=а –b=23–6=17 ед. изм. (метров) в) 10 литров варенья разложили в 2-х литровые банки. Сколько банок варенья получилось? Используем величинный подход. Объем – величина непрерывная. Длина отрезка а=10 ед. изм. показывает исходный объем, длина отрезка b=2 показывает, какой объем находится в одной банке. 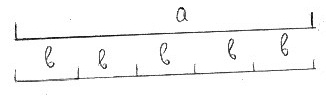 Неизвестное число банок определяется как количество равных отрезков длиной b, помещающихся в отрезке а: с=а:b= 10:2=5 (штук банок) г) Было 5 ящиков фруктов по 20 кг в каждом. Сколько килограммов фруктов было? Используем величинный подход. Масса – величина непрерывная. Длина отрезка а=20 ед. изм. показывает массу одного ящика. Длина отрезка b, составленная из 5-ти отрезков длиной а, показывает, какая масса находится во всех ящиках.  Неизвестную массу определяем как сумму длин 5-ти отрезков а: b=a+а+а+а+а=5.а=5.20=100 ед. изм. (килограммов) |
