Минимтерство развития информационных технологий и коммуникации республики узбекистан ташкентский универститет информационных технологии имени мухаммада алхоразмий
 Скачать 40.46 Kb. Скачать 40.46 Kb.
|
|
МИНИМТЕРСТВО РАЗВИТИЯ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И КОММУНИКАЦИИ РЕСПУБЛИКИ УЗБЕКИСТАН ТАШКЕНТСКИЙ УНИВЕРСТИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИИ ИМЕНИ МУХАММАДА АЛ-ХОРАЗМИЙ ОТЧЁТ №6 по предмету: Архитектура компьютера Выполнил(а):Абдумуталиев Асадбек Группа: 832-19 Принял: Яхшибоев Р.Э Ташкент – 2021 Тема: Изучение модели вычислений «операция-операнд» Цель работы: Ознакомиться с моделью вычислений в виде графа «операция-операнд» Для описания существующих информационных зависимостей в выбираемых алгоритмах решения задач может быть использована модель в виде графа «операции-операнды». Принимается: время выполнения любых вычислительных операций является одинаковым и равняется 1 (в тех или иных единицах измерения). передача данных между вычислительными устройствами выполняется мгновенно без каких-либо затрат времени (что может быть справедливо, например, при наличии общей разделяемой памяти в параллельной вычислительной системе). Представим множество операций, выполняемых в исследуемом алгоритме решения вычислительной задачи, и существующие между операциями информационные зависимости в виде ациклического ориентированного графа . 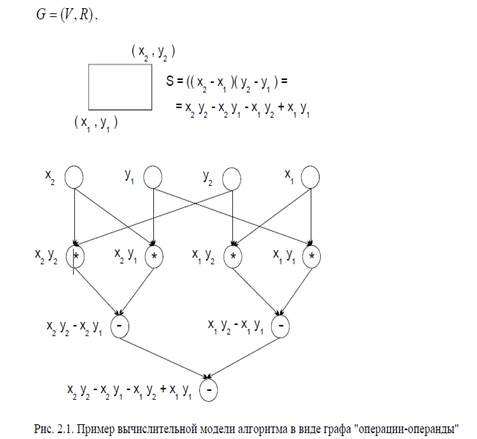 где V есть множество вершин графа, представляющее выполняемые операции алгоритма, а R есть множество дуг графа (при этом дуга ), графу только, если операция j использует результат выполнения операции i ). Для примера на рис. 2.1 показан граф алгоритма вычисления площади прямоугольника, заданного координатами двух углов. Как можно заметить по приведенному примеру, для выполнения выбранного алгоритма решения задачи могут быть использованы разные схемы вычислений и построены соответственно разные вычислительные модели. В рассматриваемой вычислительной модели алгоритма вершины без входных дуг могут использоваться для задания операций ввода, а вершины без выходных дуг - для операций вывода. Обозначим через множество вершин графа без вершин ввода, а через d(G) диаметр (длину максимального пути) графа. Описание схемы параллельного выполнения алгоритма Операции алгоритма, между которыми нет пути в рамках выбранной схемы вычислений, могут быть выполнены параллельно (для вычислительной схемы на рис. 2.1, например, параллельно могут быть выполнены сначала все операции умножения, а затем первые две операции вычитания). Возможный способ описания параллельного выполнения алгоритма может состоять в следующем. Пусть p есть количество процессоров, используемых для выполнения алгоритма. Тогда для параллельного выполнения вычислений необходимо задать множество в котором для каждой операции указывается номер используемого для выполнения операции процессора и время начала выполнения операции . Для того, чтобы расписание было реализуемым, необходимо выполнение следующих требований при задании множества : 1) один и тот же процессор не должен назначаться разным операциям в один и тот же момент времени, 2) к назначаемому моменту выполнения операции все необходимые данные уже должны быть вычислены. Время Tp выполнения параллельного алгоритма зависит от выбранного расписания и вычислительной схемы алгоритма. Рассмотрим основные показатели производительности параллельных алгоритмов. Показатели эффективности параллельных вычислений: ускорение, эффективность, масштабируемость. Ускорение (speedup), получаемое при использовании параллельного алгоритма для p процессоров, по сравнению с последовательным вариантом выполнения вычислений определяется величиной Sp(n)=T1(n)/Tp(n) т.е. как отношение времени решения задач на скалярной ЭВМ к времени выполнения параллельного алгоритма (величина n используется для параметризации вычислительной сложности решаемой задачи и может пониматься, например, как количество входных данных задачи). Эффективность (efficiency) использования параллельным алгоритмом процессоров при решении задачи определяется соотношением Ep(n)=T1(n)/(pTp(n))=Sp(n)/p (величина эффективности определяет среднюю долю времени выполнения алгоритма, в течение которой процессоры реально используются для решения задачи). Из приведенных соотношений можно показать, что в наилучшем случае Sp(n)=p и Ep(n)=1. Повышение ускорения обычно может быть обеспечено за счет увеличения числа процессоров, что приводит, как правило, к падению эффективности. И, обратно, повышение эффективности достигается во многих случаях при уменьшении числа процессоров (в предельном случае идеальная эффективность Ep(n)=1 легко обеспечивается при использовании одного процессора). При выборе надлежащего параллельного способа решения задачи может оказаться полезной оценка стоимости (cost) вычислений, определяемой как произведение времени параллельного решения задачи и числа используемых процессоров. Cp=pTp В этой связи можно определить понятие стоимостно-оптимального (cost-optimal) параллельного алгоритма как метода, стоимость которого является пропорциональной времени выполнения наилучшего параллельного алгоритма. Заключение В данной работе предоставлена информация о модели вычислений в виде графа «операция-операнд». Рассмотрен пример. А также имеется информация об основных показателей производительности параллельных алгоритмов. Список литературы: 1. https://studfile.net/preview/9100610/page:23/ 2. https://intuit.ru/studies/courses/4447/983/lecture/14931?page=11 3. https://studbooks.net/2429436/informatika/zadachi_parallelnyh_vychisleniy |
