Министерство образования и науки пермского края
 Скачать 2.1 Mb. Скачать 2.1 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ПЕРМСКОГО КРАЯ Государственное бюджетное профессиональное образовательное учреждение «Горнозаводский политехнический техникум» ИНДИВИДУАЛЬНЫЙ ПРОЕКТ по математике О, Великие математики! Обучающийся: Агафонов Данил Константинович Специальность: 15.02.08 Технология машиностроения Группа: ТМ - 108 Руководитель: Малкова Венера Александровна Горнозаводск 2018 Содержание Введение 3 Глава 1 Великие математики 5 1.1Биография математиков 5 Эварист Галуа (1811-1832) Французский математик. 5 1.2 Математические открытия 18 Глава 2 Создание стенда «О, Великие математики!» 22 2.1 Викторина «Великие математики и математические открытия» 22 2.2 Обработка результатов викторины 24 Как показал результат викторины, самый сложный вопрос для студентов нашего техникума – 1 вопрос: Главный труд этого математика «Математические начала натуральной философии». На него никто не ответил правильно. 26 На вопрос №2: По основной профессии он был юристом, а математикой занимался на досуге. - 26 2.3.Создание стенда 26 Заключение 27 1.http://www.fizmatolimp.ru/biografii.html 29 Приложение 1 29 ВведениеАктуальность исследования Математика появилась одновременно со стремлением человека изучить мир вокруг себя. Изначально она входила в состав философии - матери наук - и не была выделена как отдельная дисциплина наравне с той же астрономией, физикой. Однако с течением времени ситуация изменилась. Знаний у людей накапливалось все больше, в итоге произошло разделение точных и естественных наук. После официального "рождения" каждая из них пошла своим путем, развиваясь, укрепляя фундамент теорией, подкрепленной практикой. Казалось бы, какая практика может быть у математики, самой абстрактной из наук? Этот предмет способен описать абсолютно все процессы, происходящие на нашей планете и за ее пределами, а знание природы явления позволяет делать выводы и строить прогнозы. Отсюда можно сделать вывод, что все науки связаны между собой, наиболее очевидна эта зависимость между математикой и физикой. Поэтому в большинстве случаев великие математики и физики составляют одну группу ученых. Проблема: Изучая математику, мы очень часто сталкиваемся с именами великих ученых, но в учебнике очень мало конкретной информации о них Цель исследования: изучение биографии некоторых великих математиков и знакомство с самыми важными их открытиями. Гипотеза: студенты техникума мало знают о великих математиках и их открытиях. Задачи исследования: 1. Ознакомиться с информацией о великих математиках, их биографии и открытиях в науке. 2. Составить презентацию, содержащую портреты математиков и некоторые факты из жизни и деятельности. 3. Провести анкетирование студентов (викторину) с целью выявления знаний о великих математиках, сделавших открытия в математике. 4. Сделать выводы о результатах анкетирования 5. Создать информационный стенд о великих математиках, их биографии и открытиях в науке. Глава 1 Великие математики1.1Биография математиковЭварист Галуа (1811-1832) Французский математик. Биография: Галуа родился в Бур-ля-Рен, южном предместье Парижа. Он был вторым среди троих детей Николя-Габриэля Галуа и Аделаиды-Мари Демант. Отец был убеждённым республиканцем, и когда Эваристу исполнилось 4 года, отец стал мэром города, сохранив этот пост при реставрации монархии и далее, вплоть до 1829 года. Биография: Галуа родился в Бур-ля-Рен, южном предместье Парижа. Он был вторым среди троих детей Николя-Габриэля Галуа и Аделаиды-Мари Демант. Отец был убеждённым республиканцем, и когда Эваристу исполнилось 4 года, отец стал мэром города, сохранив этот пост при реставрации монархии и далее, вплоть до 1829 года.В возрасте 12 лет Эварист поступил в Королевский коллеж Луи-ле-Гран. В годы учёбы Галуа стал свидетелем попытки заговора учеников, придерживающихся республиканских взглядов, против руководства коллежа из-за слухов о возможном преобразовании коллежа в иезуитское училище (коим он был до революции). Заговор был раскрыт, и более ста учащихся коллежа были с позором исключен. В 15 лет он открыл для себя математику и с тех пор, по словам одного изпреподавателей, «был одержим демоном математики». Ему было неполных 18 лет, когда была опубликована его первая работа. Несмотря на свою молодость, успел сделать много открытий в математике, но, к сожалению, был убит на дуэли в 20 лет. Открытия в математике: Теория Галуа — раздел алгебры, изучающий симметрии корней многочленов. Симметрии описываются в терминах группы перестановок корней многочлена. В 17 лет опубликовал свою первую работу в журнале «Annales de Gergonne». Высказывание: Математика! Только она принесла в мою жизнь минуты счастья, которое достается очень немногим. Э. Галуа  Пьер Ферма(1601-1665) Французский математик. Биография: Пьер Ферма родился 17 августа 1601 года в гасконском городке Бомон-де-Ломань (Beaumont-de-Lomagne, Франция). Его отец, Доминик Ферма, был зажиточным торговцем-кожевником, вторым городским консулом. В семье, кроме Пьера, были ещё один сын и две дочери. Ферма получил юридическое образование — сначала в Тулузе (1620—1625), а затем в Бордо и Орлеане (1625—1631). В колледже Пьер приобрел хорошее знание языков: латинского, греческого, испанского, итальянского. Ферма славился как тонкий знаток античности. Крупную заслугу Ферма перед наукой видят, обыкновенно, во введении им бесконечно малой величины в аналитическую геометрию. Пьер де Ферма умер 12 января 1665 года в городе Кастр, во время выездной сессии суда Открытия в математике Создание теории чисел. Сформулировал теорему о возможности представления произвольного числа суммой не более четырёх квадратов Великая теорема - Для любого натурального числа n > 2 уравнение не имеет натуральных решений a, b и c. Высказывание: Природа всегда действует наиболее короткими путями. П. Ферма И  саак Ньютон(1643-1727) саак Ньютон(1643-1727)Британский физик Биография: Исаак Ньютон родился в деревне Вулсторп (англ. Woolsthorpe, графство Линкольншир) в канун гражданской войны. 1661 году Ньютон успешно окончил школу и отправился продолжать образование в Кембриджский университет. В конце 1664 года Ньютон стал бакалавром, а в 1668 году стал магистром. Ньютон стал знаменит и в январе 1672 года был избран членом Королевского общества. 28 апреля 1686 года первый том «Математических начал» был представлен Королевскому обществу. Все три тома вышли в 1687 году. С 1699 года он стал управляющим («мастером») Монетного двора. В декабре 1701 года он официально ушёл в отставку со всех своих постов в Кембридже. Исаак Ньютон умер в 1727 году во время эпидемии чумы. Открытия в математике: Универсальная арифметика Теории бесконечных рядов Анализа бесконечно малых Высказывание: Опыт - это не то, что происходит с вами; это то, что вы делаете с тем, что происходит с вами. И. Ньютон. Н  иколай Иванович Лобачевский иколай Иванович ЛобачевскийРусский математик(1792-1856) Биография: Н. И. Лобачевский родился в Нижнем Новгороде. Его родителями были Иван Максимович Лобачевский (чиновник в геодезическом департаменте) и Прасковья Александровна Лобачевская Большое влияние во время обучения в университете на Лобачевского оказал Мартин Фёдорович Бартельс — друг и учитель великого немецкого математика Карла Фридриха Гаусса. По окончании университета Лобачевский получил степень магистра по физике и математике с отличием (1811) и был оставлен при университете. В 1814 году стал адъюнктом, спустя 2 года — экстраординарным, и в 1822 году — ординарным профессором. Открытия в математике: Лобачевский пришел к выводу о возможности создания новой, непротиворечивой геометрии, которую назвал «воображаемой геометрией». Николай Иванович изменил существующую аксиому на другую. Она звучит так: “через точку, не лежащую на прямой, может проходить множество прямых параллельных с первой”. Он разработал метод приближенного решения уравнений. Также Лобачевский дал понятие о признаке сходимости рядов и о непрерывной функции. Высказывание: Ученый должен идти по непроторенным путям, несмотря на препятствия. Н. И. Лобачевский. К  арл Фридрих Гаусс(1777-1855) арл Фридрих Гаусс(1777-1855)Немецкий математик Биография: Гаусс Карл Фридрих - Иоганн Фридрих Карл Гаусс родился 30 апреля 1777г. Едва трех лет от роду он уже умел считать и выполнять элементарные вычисления. Однажды, при расчетах своего отца, который был водопроводным мастером, его трехлетний сын заметил ошибку в вычислениях. Расчет был проверен, и число, указанное мальчиком было верно. В 1784г. Карл пошел в школу. Учитель очень заинтересовался маленьким Гауссом и в 1786г. он получил из Гамбурга специальный арифметический текст. Карл покинул родительский дом в 1788г., когда поступил в школу следующей ступени. Гаусс не терял в новой школе времени даром: он хорошо выучил латынь, необходимую для дальнейшей учебы и карьеры. В 1791г. Гаусс, в качестве одаренного молодого горожанина, был представлен государю. Открытия в математике: Ему не было еще девятнадцати - доказательство того, что можно построить правильный 17 - угольник циркулем и линейкой. Метод Гаусса — классический метод решения системы линейных алгебраических. Он открыл характеристику поверхности (гауссову кривизну), которая не изменяется при изгибаниях, тем самым заложив основы римановой геометрии. Гаусс доказал, основную теорему теории поверхностей. П  етер Густав Лежён Дирихле(1805-1859) етер Густав Лежён Дирихле(1805-1859)Немецкий математик Биография: Биография Дирихле родился в вестфальском городе Дюрене в семье почтмейстера. Его предки были выходцами из бельгийского городка Ришле, этим обусловлено происхождение необычной для немецкого языка фамилии. Часть фамилии «Лежён» имеет аналогичное происхождение — деда называли «молодым человеком из Ришле ». В 12 лет Дирихле начал учиться в гимназии в Бонне, спустя два года — в иезуитской гимназии в Кёльне, где в числе прочих преподавателей его учил Георг Ом. С 1822 по 1827 г. жил в качестве домашнего учителя в Париже, где вращался в кругу Фурье. Он умер в Гёттингене, через несколько месяцев после смерти своей жены Ребекки. Открытия в математике: Он ввёл такое понятие, как «условная сходимость» и определил её признак. Доказал теорему о прогрессии. Значительно развил теорию потенциала. Внёсший существенный вклад в математический анализ, теорию функций и теорию чисел. Доказал теорему о существовании бесконечно большого числа простых чисел во всякой арифметической прогрессии из целых чисел, первый член и разность которой числа взаимно простые. Е  вклид (ок. 365 — 300 до н. э.) вклид (ок. 365 — 300 до н. э.)Греческий математик Биография: О жизни этого ученого почти ничего не известно. До нас дошли только отдельные легенды о нем. Первый комментатор «Начал» Прокл (V век нашей эры) не мог указать, где и когда родился и умер Евклид. По Проклу, «этот ученый муж» жил в эпоху царствования Птолемея I. Некоторые биографические данные сохранились на страницах арабской рукописи XII века: «Евклид, сын Наукрата, известный под именем «Геометра», ученый старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира». Его называли ”Отец Геометрии” Открытия в математике: Алгоритм Евклида Главный труд Евклида - "Начала" (по-другому "Элементы"). Все книги Евклида основываются на аксиомах - утверждениях, не требующих доказательств. Одиннадцатая аксиома - Если дана прямая и точка не лежащая на ней, то можно провести только одну прямую, проходящую через точку и не пересекающуюся с данной прямой Евклид первый начал изучать свойства простых чисел - и доказал, что их множество бесконечно. Евклид сформулировал закон прямолинейного распространения света и закон отражения, а также теорему о делении с остатком. Высказывание: Если теорему так и не смогли доказать, она становится аксиомой. Евклид. Н  ильс Хенрик Абель(1802-1829) ильс Хенрик Абель(1802-1829)Норвежский математик Биография: Рождение и учёба родился в семье пастора. Детство Абеля было омрачено слабым здоровьем, а также пьянством и постоянными раздорами его родителей. В школе, благодаря учителю Берту Михаэлю Хольмбоэ, увлёкся математикой. В 1821 году Абель поступил в университет Христиании (ныне Осло), где преподаватели, ознакомившись с его ранними работами, решили установить ему стипендию из личных средств, «дабы сохранить для науки это редкое дарование». Чтобы облегчить жизнь матери, Нильс Хенрик взял одного из братьев к себе и стал подрабатывать репетиторством. Две болезни на ложились друг на друга, и в 1829 году Нильс Хенрик Абель умер Открытия в математике: Абель закончил блестящее исследование древней проблемы: доказал невозможность решить в общем виде (в радикалах) уравнение 5-й степени. В алгебре Абель нашёл необходимое условие для того, чтобы корень уравнения выражался «в радикалах» через коэффициенты этого уравнения. Он первый определил эллиптические функции как функции, обратные эллиптическим интегралам, распространил их определения на общий комплексный случай и глубоко исследовал их свойства. Высказывание: Несомненно, ты считаешь, что плохо растрачивать столько времени на путешествие, но я не думаю, что это можно назвать словом "растрачивать" Н. Х. Абель  Готфрид Вильгельм Лейбниц(1646-1716) Немецкий философ Биография: Отфрид Вильгельм родился в семье профессора лейпцигского университета Фридриха Лейбница и Катерины Шмюк. Когда мальчику было 8 лет, его отец умер, оставив после себя большую личную библиотеку. Свободный до со теки — это сокровищницы всех богатств человеческого духа туп к книгам и врождённый талант позволили молодому Лейбницу уже к 12 годам самостоятельно изучить латынь и взяться за изучение греческого языка. В 15-летнем возрасте Готфрид сам поступил в тот же Лейпцигский университет, где когда-то работал его отец. Спустя 2 года переходит в Йенский университет, где изучает математику. 4ноября 1716 г., вследствие ухудшения здоровья, Готфрид В. Лейбниц умирает. Открытия в математики: Анализ — дифференциальное и интегральное исчисление. Он обосновал необходимость регулярно мерить у больных температуру тела. Новый метод максимумов и минимумов Используя геометрическое истолкование отношения dy/dx, он кратко разъясняет признаки возрастания и убывания, максимума и минимума, выпуклости и вогнутости, а также точки перегиба. П  ифагор (570-495г до н.э) ифагор (570-495г до н.э)Греческий философ Биография: Его отцом был некий Мнесарх из Самоса, человек благородного происхождения и образования. Родился на острове Самос около 580 года до н. э. (по другим источникам, в 586 до н. э.). Пифагор объездил весь свет и собрал свою философию из различных систем, к которым имел доступ. Так, он изучал эзотерические науки у брахманов Индии, астрономию и астрологию в Халдее и Египте. Основал общество в Кротоне, италийском городе, находившемся в тесных сношениях с Самосом. Он был ученее всех своих современников Биография Пифагора Пифагор жил в Кротоне, но несомненно, что умер он в Метапонте, куда переселился вследствие враждебного отношения кротонцев к его союзу. Открытия в математики: В геометрии: знаменитая и любимая всеми теорема Пифагора, а также построение отдельных многогранников и многоугольников. Высказывание: Лесть подобна оружию, нарисованному на картине: она доставляет приятность, а пользы никакой. Пифагор С  офья Ковалевская(1850-1891гг) офья Ковалевская(1850-1891гг)Русский математик Биография: Родилась 15 января 1850 года в Москве в имение Палибино Отец: Василий Васильевич Корвин-Круковский, генерал Мать: Елизавета Федоровна Корвина-Круковская, человек искусства. В течении двух с половиной лет она усвоила всю арифметику, затем был изучен обширный курс алгебры и на шестом году обучения была освоена геометрия Софья хотела поступить в университет, но доступ женщинам во все российские университеты был закрыт. Высшее образование она могла получить только за границей. Открытия в математике: Она открыла третий классический случай разрешимости задачи о вращении твёрдого тела вокруг неподвижной точки, которую начали Леонард Эйлер и Ж. Л. Лагранж. Она доказала существование аналитического (голоморфного) решения задачи Коши для систем дифференциальных уравнений с частными производными, исследовала задачу Лапласа о равновесии кольца Сатурна, получила второе приближение. Решила задачу о приведении некоторого класса абелевых интегралов третьего ранга к эллиптическим интегралам. Высказывание: Стоит мне только коснуться математики, как я опять забуду всё на свете. С. Ковалевская Ф  алес Милетский(конец VII - начало VI века до нашей эры) алес Милетский(конец VII - начало VI века до нашей эры)Греческий философ Биография: Сообщается, что Фалес был торговцем и много путешествовал. Некоторое время жил в Египте, в Фивах и Мемфисе, где учился у жрецов, изучал причины наводнений, продемонстрировал способ измерения высоты пирамид. Считается, что именно он «привез» геометрию из Египта и познакомил с ней греков. Его деятельность привлекла последователей и учеников, которые образовали милетскую (ионийскую) школу. Предание рисует Фалеса не только собственно философом и учёным, но также «тонким дипломатом и мудрым политиком»;. Сообщается, что Фалес был торговцем и много путешествовал. Некоторое время жил в Египте, в Фивах и Мемфисе, где учился у жрецов, изучал причины наводнений, продемонстрировал способ измерения высоты пирамид. Считается, что именно он «привез» геометрию из Египта и познакомил с ней греков. Его деятельность привлекла последователей и учеников, которые образовали милетскую (ионийскую) школу. Открытия в математике: Ему принадлежит открытие следующих теорем: Вертикальные углы равны. В равнобедренном треугольнике углы, лежащие при основании, равны. Теорема о равенстве двух треугольников по стороне и двум прилежащим к ней углам. Высказывание: Блаженство тела состоит в здоровье, блаженство ума — в знании. Ф. Милетский К  олмогоров Андрей Николаевич олмогоров Андрей Николаевич(1903-1987) Советский математик Биография: Биография Ранние годы Андрей Николаевич Колмогоров родился 12 апреля (25 апреля по новому стилю) 1903 года в Тамбове, где его мать задержалась по пути из Крыма домой в Ярославль. Андрей Николаевич Колмогоров воспитывался в Ярославле 3 сёстрами матери, одна из них, Вера Яковлевна Колмогорова, официально усыновила Андрея и в 1910 году переехала с ним в Москву для определения в гимназию. Тётушки Андрея в своём доме организовали школу для детей разного возраста, которые жили поблизости, занимались с ними, для ребят издавался рукописный журнал «Весенние ласточки». В нём публиковались творческие работы учеников — рисунки, стихи, рассказы. В нём же появлялись и «научные работы» Андрея — придуманные им арифметические задачи. Здесь же мальчик опубликовал в пять лет свою первую работу по математике. Открытия в математике: Исследования и открытия в области: Метрическая теория функций. Дескриптивная теория множеств. Математическая логика. Функциональный анализ Дифференциальные уравнения. Теория приближений. Высказывание: Я всегда считал, что истина — главное. А.Н.Колмогоров 1.2 Математические открытияВ отличие от других наук, математика, как представительница чистого разума, развивается поступательно, вне зависимости от увлечений человечества на том или ином историческом промежутке времени, от революций и катаклизмов общества. Иногда математики любят ставить проблемные вопросы, на решение которых уходят столетия. Теорема есть некое математическое утверждение, правильность которого требует построения логической цепочки доказательств, основанной на использовании законов формальной логики с привлечением аксиом – истин, принимаемых как само собой разумеющееся, очевидное и доказательств не требующее. Особого интереса заслуживают теоремы, доказательства которых вызывают сомнение или отсутствуют. Такое бывает у непререкаемых авторитетов. Ландау, например, на лекции по теоретической физике в спешке мог пропустить звено логической цепочки «как очевидное», тогда как другим теоретикам «очевидное» могло не даваться многие годы, вызывая в голове ступор. Юрист по профессии и математик по увлечению (в наше время у юристов подобные увлечения – нонсенс) Пьер Ферма (1601-1665) в письме другу, написанном в 1636 году, выдвинул любопытное утверждение из теории чисел, впоследствии получившее название Великой теоремы Ферма. На полях он оставил следующее сопровождение: «Я располагаю изумительным доказательством, но оно слишком велико для размещения на полях». То есть великий ученый прямо заявил, что доказал свою теорему. Потомкам пришлось 360 лет разбираться с тем, действительно ли Ферма доказал, или просто соврал. Благо еще удалось бы показать, что теорема неверна, найти один единственный опровергающий пример, но, несмотря на все усилия, сделать этого не удавалось. И формулировка то проще некуда: уравнение Xn+Yn=Zn не имеет целочисленных решений при n>2. При n=2 эта теорема (так называемая теорема Пифагора, предложенная ненавистником бобов более двух тысячелетий тому назад) имеет бесконечное множество решений. История доказательств Великой теоремы трагична и полна драматизма. Складывается впечатление, будто ехидный Ферма бросил вызов потомкам (открыл ящик Пандоры), а когда речь идет о деле чести, можно представить, как болезненно переживали математики-профессионалы подобную «легкомысленность» в последующие столетия. Можно без преувеличения сказать, что у математиков начался массовый психоз: «почему я не могу доказать то, что доказал Ферма черт знает в какие примитивные времена?» Увлечение превращалось в цель и смысл жизни. Некоторые в буквальном смысле свихнулись на этом. Перед теоремой пасовали даже такие гиганты мысли, как Гаусс, Леонард Эйлер, доказавший теорему для n=3 и 4, Лежандр (n=5), Дирихле (n=6)… После того, как в 1907 году состоятельный немецкий любитель математики, наподобие Нобеля, завещал 100 тысяч марок тому, кто докажет Великую теорему, и вовсе начался массовый ажиотаж. Выскочек без образования презрительно называли ферматистами, а говорить о теореме Ферма в высшем математическом свете стало признаком дурного тона, вроде как нецензурно выругаться. Однако в тиши кабинетов и великие прикладывались к «запретному зелью». Мало-помалу появились доказательства для степени n<100, n<619… все невероятно сложные и длинные. В эти смутные времена в Японии жил математик Ютака Танияма. Когда ему исполнилось 28 лет, он выдвинул гипотезу (впоследствии получившую название гипотезы Танияма-Шимура-Вейла), что каждой эллиптической кривой соответствует определенная модулярная форма. Гипотеза, казалось, не имеет отношения к теории чисел, она соединяла понятия двумерных и четырехмерных форм: уравнения двух абсолютно разных математических объектов можно разложить в одинаковые математические ряды. После выступления Танияма на международном математическом конгрессе, состоявшемся в Токио в1955 году, и демонстрации соответствия нескольких эллиптических кривых модулярным формам, многие увидели в этом не более чем забавное совпадение. Через три года Танияма покончил жизнь самоубийством, и о гипотезе забыли. А в 1985 году произошла революция – немец Герхард Фрей опубликовал следующее заявление: «Если доказать гипотезу Танияма, тем самым будет доказана и Великая теорема Ферма». Заявление Фрея через год удалось строго доказать профессору калифорнийского университета Риббету. Поскольку, однако, у математиков уже сложилась аллергия на теорему Ферма, возиться с доказательством гипотезы Танияма, из которой следует верность теоремы Ферма, из соображений сложности не хотелось. Чем гипотеза Танияма должна быть проще теоремы Ферма? Поток гениев, однако, не остановить. Как настоящий ученый, английский профессор математики Эндрю Уайлс, зная историю, не обольщался результативностью своих изысканий в области доказательства гипотезы Танияма. Позже он признавался, что работу над Великой теоремой скрывал даже от жены. И все-таки 23 июня 1993 года он набрался храбрости, надел на голову петлю и на математической конференции по теории чисел в Кембридже громогласно объявил о достижении цели. Такой наглости никто из присутствующих не ожидал от не очень известного математика. Тотчас подключилась пресса. Состоялась публичное доказательство теоремы Танияма, а следовательно и теоремы Ферма. Ошибок никто не обнаружил. Следовательно, масштабное событие произошло: Великая теорема доказана. Но, по закону подлости, за два дня до публикации, хитрый коллега Уайлса Кац, заметил, что «один фрагмент рассуждений опирается на систему Эйлера, на самом деле таковой не являясь». Это была катастрофа. Бедный Уайлс понял, что проиграл, и ему оставалось либо повеситься, чтобы не остаться навсегда осмеянным потомками, либо бросить занятия математикой, сменить имя, сделать пластическую операцию и уехать на край земли, где математические проблемы людям, как говорится, по барабану. Уайлс впал в депрессию: как смотреть коллегам в глаза? Он отказывался от пищи и здоровье его ухудшалось. Но в сентябре 1994 года, размышляя над узким местом доказательства Уайлса, его коллега Тейлор из Оксфорда неожиданно обнаружил, что если заменить систему Эйлера на теорию Ивасава, то все сойдется. Около года математики изучали непротиворечивость доказательства Уайлса с замечанием Тейлора, и летом 1995 года в ведущем математическом журнале «Анналы математики» было опубликовано доказательство гипотезы Танияма, занявшее целый номер. Итак, в 1995 году мир признал, что Эндрю Уайлс доказал Великую теорему Ферма. Уайлс оказался тем счастливчиком, которому удалось нанести последний нокаутирующий удар по проблеме. Но не следует забывать, что за ним стоят все великие математики предыдущих столетий. Если кому-то покажется незначительность этого события, достаточно вспомнить, что математика стоит в авангарде всех научных достижений, а решение казалось бы «легкомысленной задачи» порождает целые направления в развитии математики. Леонардо да Винчи однажды заметил, что «наукой можно назвать только математически подтвержденное учение». Так все-таки доказал Ферма свою теорему, или это была гипотеза? Возможно, ему показалось, что доказал, но на самом деле ошибся. Сознательно соврал, упоенный красотой открытия? И этого исключить нельзя. Все же большинство математиков склоняются к мысли, что во времена Ферма нельзя было придумать альтернативное доказательство, как нельзя в эпоху дилижансов и рыцарских турниров изобрести атомную бомбу. Ферма не доказал, но гениально угадал! С точки зрения морали, из этой очень поучительной истории следует хотя бы тот маленький вывод, что, внимая пламенной риторике ведущих авторитетов в своей области, каждый имеет право усомниться в справедливости сладкоречивых слов говорящего. Глава 2 Создание стенда «О, Великие математики!»2.1 Викторина «Великие математики и математические открытия»Я изучил биографии Великих математиков и историю математических открытий. После этого я составил вопросы викторины по этой теме. Викторина для студентов ГБПОУ «ГПТ» Автор-составитель: Студент группы ТМ-108 Агафонов Д.К. Вопросы: Главный труд этого математика «Математические начала натуральной философии» a) Пифагор б)Архимед в)Ньютон г)Гаусс По основной профессии он был юристом, а математикой занимался на досуге а)Евклид б)Ньютон в)Вейерштрасс г) Ферма Впервые вычислил число и доказал, что оно одинаково для любого круга а) Пифагор б) Архимед в) Евклид г) Гаусс Его считали математиком-универсалом, так как он сделал множество открытий в самых разных областях математики а) Архимед б) Евклид в) Пифагор г) Чебышев Кому принадлежат слова « Для того, чтобы быть настоящим математиком, нужно быть поэтом в душе» ? а) Колмогоров б) Ковалевская в) Чебышев г) Гаусс Ввёл многие понятия и символы, употребляемые в математике и сейчас а) Лейбниц б) Лобачевский в) Гаусс г) Колмогоров Имел титул одного из семи мудрецов Греции а) Фалес б) Архимед в) Пифагор г) Гаусс Основатель научных школ по теории вероятностей и теории функций а) Лобачевский б) Фалес в) Колмогоров г) Чебышев Один из создателей математического анализа, проективной геометрии а) Чебышев б) Паскаль в) Колмогоров г) Гаусс Его «великая теорема» - одна из самых популярных теорем математики а) Гаусс б) Ферма в) Ньютон г) Декарт Написал большой труд по геометрии « Начала» (13 книг) а) Архимед б) Евклид в) Чебышев г) Гаусс Создал новую геометрическую систему, известную под названием геометрии … Его называли «Коперником геометрии» а) Вейерштрасс б) Лобачевский в) Евклид г) Ньютон. 2.2 Обработка результатов викториныСобрав ответы студентов на вопросы викторины, я обработал данные и получил следующий результат: количество набранных баллов и точность ответа на поставленный вопрос. Количество набранных баллов За каждый правильный ответ можно получить 1 балл. Максимальное количество баллов – 12. В исследовании принимали участие все группы 2 курса и группа ТМ – 108 (1 курс).
Самое большое количество баллов набрали студенты групп ТМ – 108 и ТП - 210 (6 баллов) 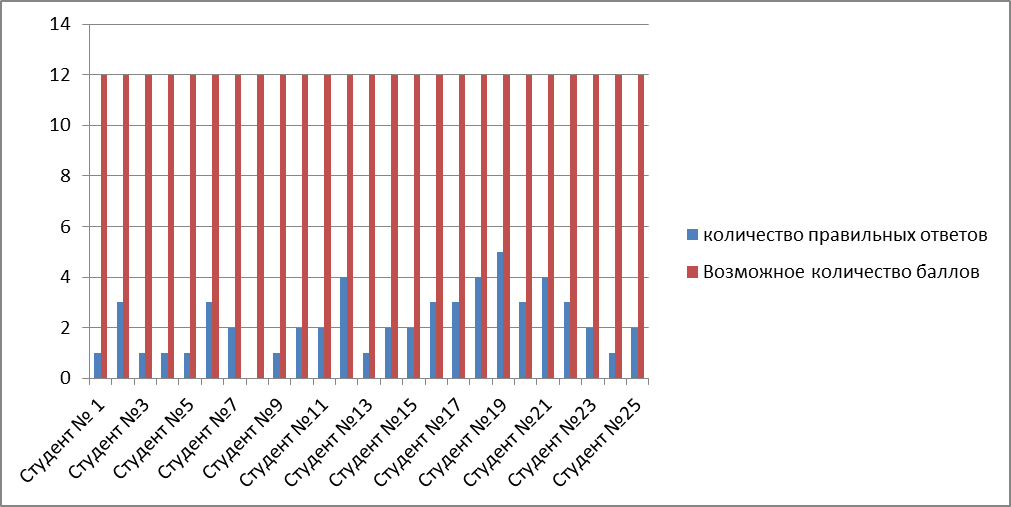 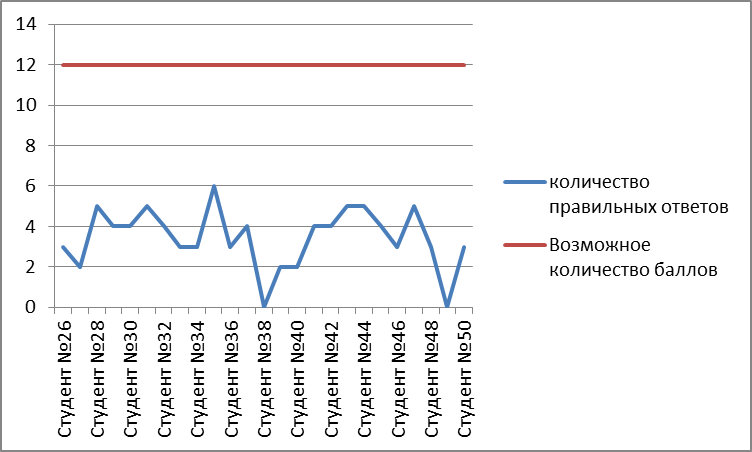 Правильные ответы на вопросы
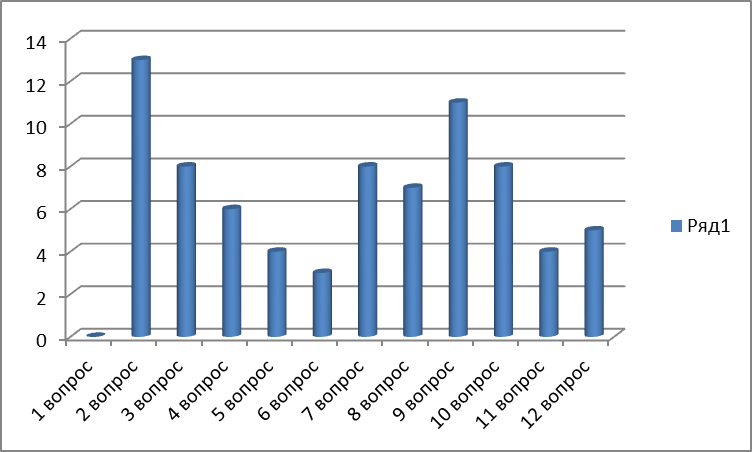 Как показал результат викторины, самый сложный вопрос для студентов нашего техникума – 1 вопрос: Главный труд этого математика «Математические начала натуральной философии». На него никто не ответил правильно.На вопрос №2: По основной профессии он был юристом, а математикой занимался на досуге. -ответили правильно 13 студентов. 2.3.Создание стендаПроанализировав результаты викторины, мы решили создать стенд в кабинет математики. Для начала мы определились с количеством и Именами математиков, которые будут на нашем стенде. Выбор наш пал на ученых, которые внесли наибольший вклад в создание алгебры и геометрии школьного курса (10-11 класс). У нас получилось 19 математиков. Теперь я изучил и поработал с информацией об этих ученых. Я оставил краткую биографию, портрет, открытие и высказывание математика. Следующим этапом стало создание самого стенда, подходящего по размерам, дизайну. На стенде нужно разместить 19 файлов формата А4. Я измерил длину и ширину этого файла. Я решил расположить их в форме прямоугольника 4 х 5. Недостающий файл на стенде, я компенсирую эпиграфом и актуальностью моей темы. Для стенда я взял термоплиту, оклеил ее клейкой пленкой, края спрятал под пластиковые уголки. Наклеил кармашки и вставил в них информацию о выбранных Великих математиках. Также прикрутил уголки для того, чтобы стенд можно было повесить на стену. Заключение Жизнь великих учёных так тесно переплелась с наукой, что уже невозможно представить математику без Пифагора, а Лобачевского – без математики. Но всё же мы надеемся, что факты из их биографий составят более полные образы учёных, которым ничто человеческое не чуждо. Математика – уникальная наука. Она способствует выработке адекватного представления и понимания знания. “Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства” – писал Леонардо да Винчи. В ходе своего исследования, я достиг поставленной цели. Все поставленные задачи я выполнил, а именно: 1. Ознакомился с информацией о великих математиках, их биографии и открытиях в науке 3. Провел анкетирование студентов (викторину) с целью выявления знаний о великих ученых, сделавших открытия в математике 4. Сделал выводы о результатах анкетирования, построил таблицы и графики 5. Создал информационный стенд о великих математиках, их биографии и открытиях в науке. Список использованных источников http://www.fizmatolimp.ru/biografii.html http://obrazovaka.ru/category/matematiki http://fb.ru/article/170806/velikie-matematiki-i-ih-otkryitiya https://math-city.nethouse.ru/articles Приложение 1 Ответы к викторине
|
