Методы системного анализа решение ЗЛП. МС индивидуальное задание №1 Голубев Д.Р. Б04-011-1. Минобрнауки россии федеральное государственное бюджетное

• Название: Минобрнауки россии федеральное государственное бюджетное
• Анкор: Методы системного анализа решение ЗЛП
• Дата: 02.12.2021
• Размер: 62.84 Kb.
• Имя файла: МС индивидуальное задание №1 Голубев Д.Р. Б04-011-1.odt
• Тип: Документы; #289128

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное

образовательное учреждение высшего образования

«Ижевский государственный технический университет

имени М.Т.Калашникова»

(ФГБОУ ВО «ИжГТУ имени М.Т.Калашникова»)

Кафедра «Системный анализ и управление качеством»

Индивидуальное домашнее задание №1

Вариант №6

Выполнил:

Студент группы Б04-011-1

Голубев Д.Р.

Проверил:

Кандидат ф.-м.н, доцент

Королев С.А

Ижевск, 2020

СОДЕРЖАНИЕ

Содержательная постановка задачи………………………………………………...3

Концептуальная постановка задачи………………………………………………...3

Математическая постановка задачи………………………………………………...3

Выбор метода решения…………………………………………………….……..…5

Проверка корректности и адекватности модели…………………………………...5

Проведение численных исследований……………………………………………...5

Вывод…………………………………………………………………………………5

1. Содержательная постановка задачи

Разработать математическую модель, описывающую движение заряженной частицы в магнитном поле.

Модель должна определить:

· Нахождение начальной скорости частицы

· Нахождение решения задачи

Исходные данные:

· Удельный заряд частицы

· Индукция магнитного поля

· Угол поворота вектора скорости

· Относительное изменение радиуса траектории частицы

· Путь, пройденный частицей

2. Концептуальная постановка задачи

· Объект исследования - частиц с удельным зарядом в однородном магнитном поле (камере Вильсона);

· Частицу будем считать абсолютно твердым телом сферической формы;

· Поле со временем выключают;

· Движение частицы будем описывать с помощью силы Лоренца, которая обеспечивает движение по окружности с центростремительным ускорением, и сила сопротивления со стороны окружающего водяного пара.

Угол поворота вектора скорости меняется на 90 градусов.

3. Математическая постановка задачи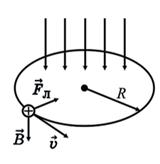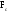




Рис. 1 Математическая модель движения частицы.

На частицу действуют 2 силы: сила Лоренца F_Л , которая обеспечивает движение по окружности с центростремительным ускорением и сила сопротивления со стороны окружающей среды.

Уравнение движения под действием F_Л:

, (1)

где v – скорость, q – заряд, m – масса, R – радиус кривизны траектории движения частицы.

(2)

при малом относительном изменении радиуса кривизны (ΔR/R=E/100%=0.1%):

, (3)

где v₀ – начальная скорость частицы.

Сила сопротивления F_c=kv, где k – константа.

Уравнение движения частицы вдоль траектории имеет вид:

kvdt=-mdv (4)

Поскольку vdt=dS (отрезок пройденного частицей пути)

(5)

(6) (7)

Отсюда:

(8)

После выключения магнитного поля на частицу действует только F_с, поэтому:

, а (9)

Решение уравнения движения в конечных приращениях будет иметь вид:

(10)

Исходя из (8) и (10) найдем начальную скорость v₀: (11)

4. Выбор метода решения: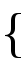

Аналитический метод, система уравнений решается методом подстановки: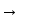




5. Проверка корректности и адекватности модели.

Вследствие простоты модели адекватность обосновывается применением известных законов и оценкой результатов расчетов



6. Проведение численных исследований

Исходные данные: d=10⁸ Кл/кг; B=10^-2 Тл; E=5%; L=30см

Найти: v₀ - ?



Вывод: Была составлена математическая модель движения заряженной частицы в магнитном поле, найдена скорость вхождения в магнитное поле (начальная скорость v₀). Выведенные формулы были проверены, результаты вычислений являются адекватными.