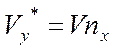Материалы к динамике полёта с формулами++++. Система уравнений движения Углы, определяющие положение летательного аппарата относительно вектора скорости Угол атаки
 Скачать 1.48 Mb. Скачать 1.48 Mb.
|
|
Система уравнений движения Углы, определяющие положение летательного аппарата относительно вектора скорости Угол атаки α - угол между связанной осью и проекцией вектора скорости на плоскость симметрии ЛА. Угол скольжения β - угол между вектором скорости и плоскостью симметрии ЛА. Знаки углов атаки и скольжения определены на рис. 4. Углы, определяющие положение летательного аппарата относительно Земли По определению нормальной и связанной систем координат положение ЛА относительно Земли определяется углами между осями связанной и нормальной системы координат. Угол тангажа υ–угол между связанной осью и горизонтальной плоскостью ; Угол рыскания ψ –угол между осью и проекцией связанной оси на горизонтальную плоскость ;
Угол крена γ – угол между связанной осью и осью смещенной в положение, соответствующее нулевому углу рыскания. Знаки углов определены на рис. 3. Воздушная скорость летательного аппарата – скорость центра масс (начала О связанной системы координат) относительно воздушной среды, не возмущенной летательным аппаратом. Земная скорость летательного аппарата – скорость центра масс (начала О связанной системы координат) относительно выбранной земной системы координат. Путевая скорость летательного аппарата – проекция земной скорости летательного аппарата на горизонтальную плоскость. Траекторные углы Угол пути ψ – угол между осью и путевой скоростью летательного аппарата (рис.5) В продольном движении центра масс на самолет как на любое тело, действуют четыре силы, условно приложенные в центре масс. Эти силы фактически являются суммой сил, действующих на различные элементы самолета.
1. Сила тяжести (земная система координат) 2. Подъемная сила 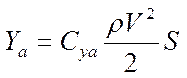 (скоростная с-ма координат) (скоростная с-ма координат)3. Сила сопротивления 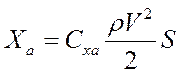 (скорост. с-ма координат) (скорост. с-ма координат)4. Сила тяги двигателей - режим работы двигателей. Система уравнений движения Уравнения движения записываются в проекциях на скоростную систему координат
Поскольку , равно центростремительному ускорению - мал, - мал, то уравнения (1), (2) можно переписать в виде:
Для определения ЛТХ нужно добавить переход от скоростной системы к земной, а также отдельное уравнение для расхода топлива.
Получим систему из дифференциальных уравнений (опуская индекс «а», т.е. , ):
- секундный расход топлива двигателя, задается в виде: 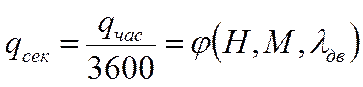 , , Из решения уравнений (1)-(6) можно найти показатели ЛТХ: Эти уравнения решаются, как правило, методами численного интегрирования, для чего необходимо записать еще ряд аналитических и графических зависимостей:
Система уравнений (1) – (13) содержит 15 неизвестных, т.е. две неизвестных должны быть заданы и называются управлениями. Для типового профиля полета задаются: 1)
Взлет: 2) Набор высоты: 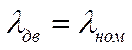 . .3) Крейсерский полет: а.) б.) 4) Снижение (планирование): 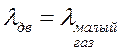 . .5) Заход на посадку: На предварительных этапах проектирования система уравнений (1) – (13) обычно решается приближенными методами. Для этого вводятся допущения для режимов 2, 3, 4: , . Параметры скорость и угол наклона траектории меняются медленно для транспортных магистральных самолетов. Кроме того, в ряде случаев можно считать, что угол мал, т.е. , .
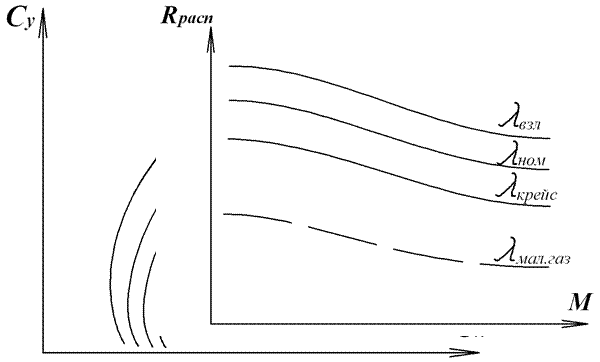
3. Расчет летно-технических характеристик (ЛТХ) Расчет основных ЛТХ включает: - определение эксплуатационной области высот и скоростей полета: максимальной и минимальной скорости, практического потолка; - расчет расхода топлива, времени и дальности полета на участках набора крейсерской высоты 2, снижения 4, крейсерского полета 3, в том числе расхода топлива на взлет 1, предпосадочный круг и посадку 5. (рис. - типовой профиль полета); - определение общей практической дальности и продолжительности полета. 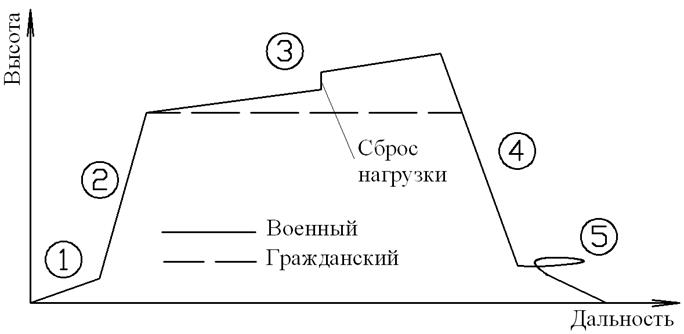 Типовой профиль полета
Часто уравнения (1) и (2) преобразуют:
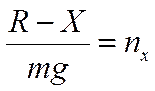 - продольная перегрузка, - продольная перегрузка,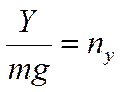 - поперечная перегрузка. - поперечная перегрузка.Тогда получим уравнения движения, выраженные через перегрузки:
Остальные уравнения (3)-(13) остаются в том же виде. Упрощение уравнений (1) и (2)
Умножим обе части уравнения (1) на :
В уравнении величина по внешнему виду соответствует 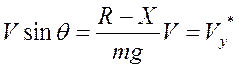 описывает «фиктивную» вертикальную скорость набора высоты (ее называют также избыточной удельной мощностью) описывает «фиктивную» вертикальную скорость набора высоты (ее называют также избыточной удельной мощностью)
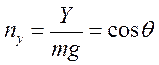 ( , полет горизонтальный). ( , полет горизонтальный).Это условие соответствует «квази»-горизонтальному полету с постоянной скоростью (т.к. ). Таким образом, для участков профиля полета 2 – набор высоты, 3 – крейсерский полет 4 – снижение для расчетов параметров И уравнения (1) и (2) из дифференциальных превращаются в алгебраические
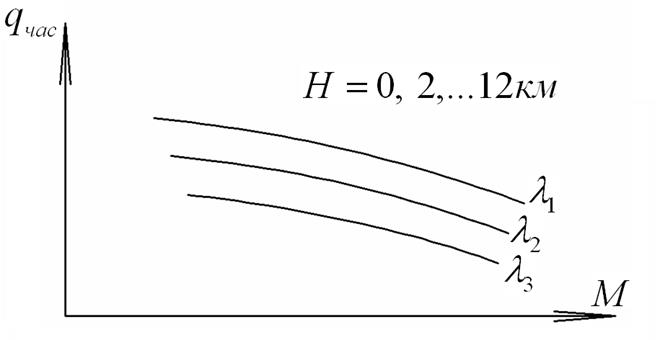
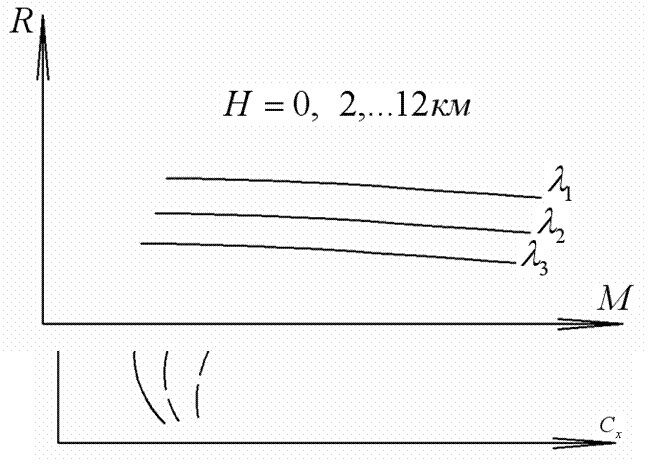
Остальные уравнения остаются в прежнем виде. Первым этапом расчетов является построение совмещенных графиков потребных тяг (сопротивления самолета) и располагаемых тяг силовой установки. В уравнении 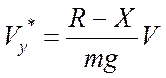 , ,где - располагаемая тяга двигателя, - тяга, потребная для горизонтального полета.
Исходные данные (для среднемагистрального с-та):
|

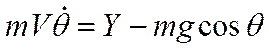
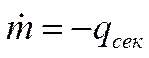
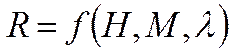
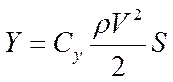
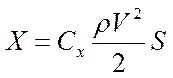
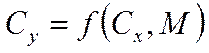
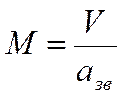
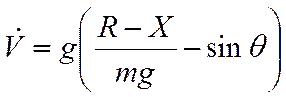
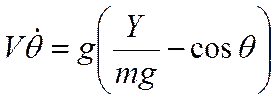
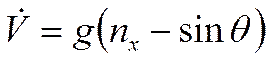
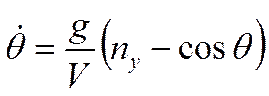
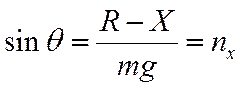
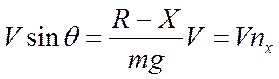
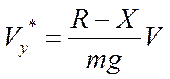 или
или