ДЗ 3 Аналитическая химия. ДЗ 3 аналит. мирэа российский технологический университет
 Скачать 148.76 Kb. Скачать 148.76 Kb.
|
Институт тонких химических технологий им. М.В. Ломоносова Кафедра аналитической химии им. И.П. Алимарина Домашнее задание №3 «Статистическая обработка результатов анализа» Вариант № 11
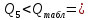 промахов нет промахов нетРассчитаем среднее значение: 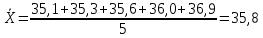 мг/мл мг/мл Рассчитаем стандартное отклонение и относительное стандартное отклонение: 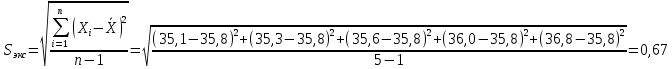 мг/мл мг/мл 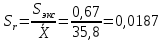 В данном случае Sr методики задано, следует проверить по 2-критерию, достигнута ли требуемая воспроизводимость: 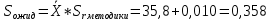 мг/мл мг/мл 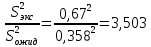 Сравним с табличным значением критерия и сделаем вывод о достижимости требуемой воспроизводимости: 2(p=0,95; f=n-1=4) = 9,488 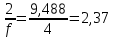 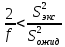 Поскольку табличное значение критерия меньше, чем рассчитанное для выборки Sr методики, то требуемая воспроизводимость не достигнута. Рассчитаем доверительный интервал: поскольку требуемая воспроизводимость не достигнута, то рассчитываем доверительный интервал по следующей формуле: 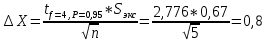 мг/мл мг/мл Запишем полную запись результатов: 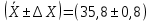 мг/мл (P=0,95; n=5) мг/мл (P=0,95; n=5)Оценим величину случайной погрешности: Абсолютная случайная погрешность: 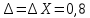 мг/мл мг/млОтносительная случайная погрешность:  Оценим правильность анализа и величину систематической погрешности: Рассчитаем экспериментальное значение коэффициента Стьюдента 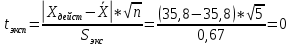 Сравним с табличными значением критерия и сделаем вывод о наличии правильности в анализе: 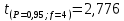 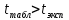 (2,776>0) – систематическая погрешность на фоне случайной не выявлен, анализ выполнен верно. (2,776>0) – систематическая погрешность на фоне случайной не выявлен, анализ выполнен верно.II. Обработка второй серии Поскольку, для второй серии задано среднее значение и стандартное отклонение, то нам следует рассчитать только относительное стандартное отклонение и доверительный интервал: 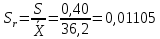 мг/мл мг/млТ.к. Sr методики не задано, поэтому рассчитаем доверительны интервал по известной формуле: 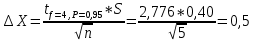 мг/мл мг/млЗапишем полную запись результатов: 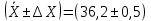 мг/мл (P=0,95; n=5) мг/мл (P=0,95; n=5)Оценим величину случайной погрешности: Абсолютная случайная погрешность: 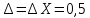 мг/мл мг/млОтносительная случайная погрешность: 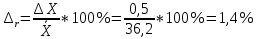 Оценим правильность анализа и величину систематической погрешности: Рассчитаем экспериментальное значение коэффициента Стьюдента 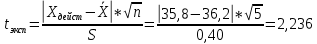 Сравним с табличными значением критерия и сделаем вывод о наличии правильности в анализе: 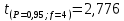 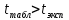 ( (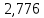 > >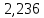 ) – систематическая погрешность на фоне случайной не выявлен, анализ выполнен верно. ) – систематическая погрешность на фоне случайной не выявлен, анализ выполнен верно.Задание №2 Для того чтобы выяснить значимо ли расхождение между результатами определений двух серий следует использовать критерий Фишера (F–критерий) для проверки однородности дисперсий и t–критерий (значение коэффициента Стьюдента) для проверки принадлежности средних одной генеральной совокупности. Проверка однородности дисперсий по критерию Фишера: Рассчитаем экспериментальное значение критерия Фишера (S2 ˃ S1): S2 (из первой серии)=0,67 мг/мл S1 (из второй серии)=0,40 мг/мл 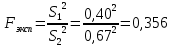 Сравним с табличным значением критерия и сделаем вывод об однородности дисперсий: F(P=0,95; f1=4; f2=4) =6,388 Fтабл > Fэксп (6,388>0,356) – стандартные отклонения принадлежат одной выборке. Проверка принадлежности средних значений одной генеральной совокупности, используя экспериментальное значение коэффициента Стьюдента: Рассчитаем средневзвешенное стандартное отклонение: 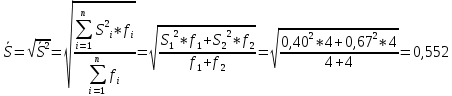 мг/мл мг/млРассчитаем экспериментальное значение коэффициента Стьюдента: 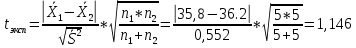 Сравним с табличным значением критерия и сделаем вывод о принадлежности средних значений одной генеральной совокупности: t(P=0,95; f=n1+n2-2=8)=2,306 tтабл > tэксп (2,306>1,146) – средние значения принадлежат одной выборке. Рассчитаем среднее значение: 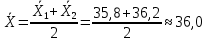 мг/мл мг/млРассчитаем доверительный интервал: 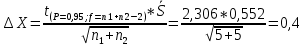 мг/мл мг/млПолная запись результатов: 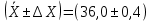 мг/мл (P=0,95; n=10) мг/мл (P=0,95; n=10)Задание №3 Расчеты будем проводить на примере первой выборки. При снижении погрешности анализа вдвое, доверительный интервал также должен уменьшиться вдвое: 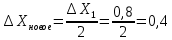 мг/мл мг/млДля простоты дальнейших расчетов примем, что стандартное отклонение практически не изменяется с увеличением числа параллельных определений. Рассчитаем «критическое» значение отношения: 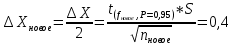 мг/мл мг/мл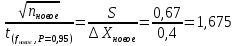 Составим таблицу и подбираем значение nновое и t(P = 0.95; f ) таким образом, чтобы соотношение было больше или равно 1,675: 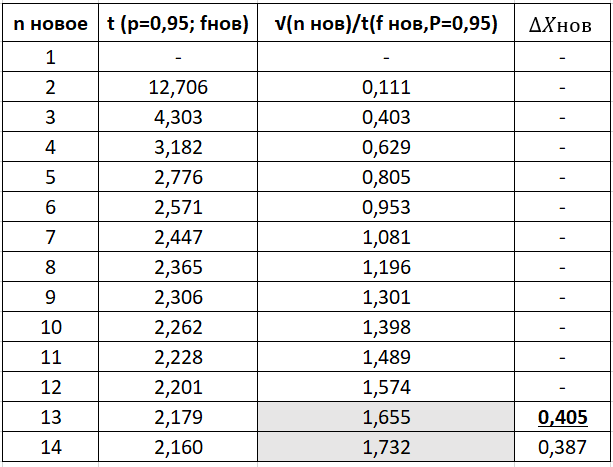 Проверка осуществляется по формуле: 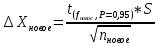 Следовательно, для снижения погрешности анализа вдвое нам следует провести 13 параллельных измерений. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


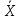 = 36,2 мг/мл
= 36,2 мг/мл