Документ. Мнемотехника на уроках математики
 Скачать 148.37 Kb.
|
|
«Мнемотехника на уроках математики» В современной трактовке мнемоника обозначает совокупность приемов и методов запоминания информации, применяемых в той или иной системе. Важнейшие принципы мнемотехники. В основе развитой памяти лежат два основных фактора- воображение и ассоциация. Для того, чтобы запомнить что-то новое, вам необходимо соотнести это новое с чем-то, т.е. провести ассоциативную связь с каким-то уже известным фактором, призвав на помощь своё воображение. Ассоциация-это мысленная связь между двумя образами. Причина, заставившая обратиться к мнемотехнике- это громоздкие логические рассуждения на уроках математики, и сложная терминология а как следствие этого- у учащихся потеря интереса к уроку, к предмету. Текст учебника математики отличается от других учебников тем, что он насыщен формулировками. Дети с большим трудом запоминают формулировки теорем, правил и алгоритмов выполнения того или иного действия, они их не учат дословно, упуская порой важные слова или искажая смысл. Для заучивания формул и правил важно научить школьников пользоваться мнемоническими правилами. Мнемоника - искусство запоминания - помогает выучить громоздкие формулы или правила, переводя их на язык смешных ассоциаций, созвучных фраз или стихов. Основные приёмы: Нахождение ярких необычных ассоциаций (картинки, фразы) ,которые соединяются с запоминаемой информацией. Всем известно БИССЕКТРИСА-это крыса, Которая бегает по углам И делит угол пополам. ВЫСОТАпохожа на кота, Который, выгнув спину, И под прямым углом Соединит вершину И сторону хвостом. МЕДИАНА- обезьяна,> Лазает по сторонам И делит их пополам> 2. В формулах приведения можно спросить у ослика: «Надо ли менять название функции на кофункцию?» Если угол а прилежит к вертикальному диаметру (90°  a), (270° a), то ослик будет кивать вдоль вертикальной оси и отвечать «да», а если угол а прилежит к горизонтальному диаметру, то ослик поворачивает голову слева направо и отвечает «нет». Вторая часть правила требует определить знак первоначальной функции от сложного аргумента.Еще одно шуточное правило для запоминания формул приведения: Если ГО, то О, Если ВЕ, то МЕ. Если ось ГОризонтальная, то функция Остаётся неизменной, например: sin (π+x) = -sin (x). Если ось ВЕртикальная, то функция МЕняется на кофункцию, например: tg (3π/2-x) = ctg (x). (Необходимо также определить знак приведенной функции) Правило, помогающее запомнить название осей координат :ось Ординат (при произношении буквы О движение губ показывает вертикальную ось, а при произношении буквы А- горизонтальную ось , ось Абцисс ). В качестве инструмента для синтезирования сложной информации, а учителю – в качестве среза оценки понятийного и словарного багажа учащихся можно предложить составить синквейн. Слово «синквейн» происходит от французского «пять». Это стихотворение из пяти строк,
Теорема Пифагора Геометрия, 7 класс. Пифагор, наверное, любил играть в пятнашки. Помните такую игру? В квадратной коробочке нужно передвигать маленькие квадратики с числами. Сделайте «пятнашки» из четырех одинаковых прямоугольных треугольников разного цвета, которые можно свободно перемещать в квадратной коробочке. Получится наглядное пособие для демонстрации теоремы Пифагора, а также для тренировки воображения. Математические образы – это схемы, графики, геометрические фигуры. Чтобы запоминать математические понятия, нужно тренировать свое воображение манипулировать математическими образами.
На (рис.1) исходное положение треугольников. Четыре треугольника образуют черный квадрат в центре. Смещайте пальцем желтый треугольник в сторону голубого треугольника. А красный и зеленый – в нижний правый угол (рис. 2). В результате перестановки треугольников площадь черного квадрата распределилась между площадями двух других черных квадратов, меньших по размеру. Такие перестановки треугольников нужно уметь делать в своем воображении, с помощью визуального мышления. Представьте исходное положение треугольников (рис. 1). Мысленно переместите желтый треугольник. Мысленно переместите красный и зеленый треугольники. Представьте конечное положение треугольников (рис. 2). Формула площади треугольника «читается» по картинке прямоугольника. Площадь треугольника равна половине площади прямоугольника. 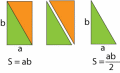 Из четырех одинаковых прямоугольных треугольников составляем большой квадрат (рис. 4), в центре которого также получается квадрат. По картинке видно, что площадь сине-зеленого квадрата равна ( a + b)^2. Ведь сторона квадрата образована двумя катетами разных треугольников, a и b. |
