Основные понятия теории множеств и способы их задания. Парадокс Рассела. Операции над множествами: объединение, пересечение, разность и симметрическая разность, дополнение. Свойства операций и принцип двойственности (правила Моргана).
Ответ:
Множество – это совокупность некоторых объектов, называемые элементами множества.
Способы задания множества: 1)Перечисление элементов 2)Характеристический предикат. � = �/
�(�)
Задания множества с помощью
«порождающей» (генерирующей» процедуры (алгоритма).
Парадокс Рассела: "Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли K само себя в качестве элемента? Если да, то, по определению K, оно не должно быть элементом K — противоречие. Если нет — то, по определению K, оно должно быть элементом K — вновь противоречие".
Операции над множествами:
Объединение множеств А и В будем называть множество С, содержащее те и только те элементы, которые принадлежат множеству А или множеству В. (С= А∪ В)
Пересечение множества А и В будем
называть множество С, содержащее только те элементы, которые принадлежат и А, и В. (С= А∩ В)
Разностью двух множеств А и В будем
называть новое множество С, обозначаемое С=А\В, которое содержит те элементы множества А, которых нет в множестве В. Множество, обозначаемое С= А△В= (А\ В) ∪ (В\ А)
Дополнение: �¯ = � � ∉ �}..
Свойства операций:
А∪ В= В∪ А А∩ В= В∩ А
Коммутативность
А∪ В ∪ С= А∪ (В∪ С)
2)
А∩ В ∩ С= А∩ (В∩ С)
Ассоциативность
А∪ В ∩ С= (А∩ С) ∪ (В∩ С)
3)
А∩ В ∪ С= (А∪ С) ∩ (В∪ С)
Дистрибутивность
4) А¯¯¯∪¯¯В¯ = А¯ ∩ В¯ Правило де
А¯¯¯∩¯¯В¯ = А¯ ∪ В¯
Моргана
А∪ В ∩ А= А
5)
А∩ В ∪ А= А
6) А∪ А= А А∩ А= А
Идемпотентность
7) А∪ ∅ = А
А∩ ∅ = ∅
8) А∪ � = � А∩ � = А А∪А¯ = �
9)
А∩А¯ = ∅
А" = А
10)
А\ В= А∩В¯
|
Сравнение множеств. Диаграммы Эйлера- Венна. Разбиения и покрытия: принцип Гейне-Бореля-Лебега – лемма «о конечном подпокрытии». Алгебра подмножеств: булеан и универсум, счетные множества и их свойства. Несчетные множества и множества «мощности континуума». Теорема Кантора.
Ответ: Сравнение множеств:
Множество А называется подмножеством множества В, если все элементы множества А содержатся во множестве В.
Два множества называются равными, если они содержат одинаковые наборы элементов.
ТЕОРЕМА:
Пустое множество Ø является подмножеством всех множеств.
Универсальное множество U содержит все множества.
Если А⊂ В, то В надмножество А.
Разбиения и покрытия: принцип Гейне-Бореля- Лебега – лемма «о конечном подпокрытии»: В любой системе интервалов, покрывающей отрезок, имеется конечная подсистема, покрывающая этот отрезок.
Множество всех подмножеств называется булеаном множества М и обозначается 2m=P(M).
Универсум — множество, содержащее все мыслимые объекты.
Множество А называется счетным, если между множеством А и множеством натуральных чисел N можно установить взаимно однозначное соответствие «на». Другими словами должен существовать алгоритм, по которому элементы этого множества могут быть переименованы. �2� = �2� = 2�/� ∋ � Свойства:
Из любого бесконечного множества X можно извлечь счетное подмножество А.
Любое множество В счетного множества А являетя конечным либо счетным.
Конечное(либо счетное) объединение счетных множеств дает в результате вновь счетное множество.
Множество рациональных чисел счетно.
Теорема Кантора: Отрезок [0;1] является не счетным множеством.
|
Отношения. Упорядоченные пары. Прямое произведение множеств, бинарные отношения (обратное,дополнение,тождественное,универсальное)
. Композиция и степень отношений, ядро отношения. Свойства отношений.
Ответ: Упорядоченной парой, обозначаемой (a,b), будем называть a и b связанных между собой свойствами:
1) if(a,b)=(c,d)(a=c)&(b=d)
2) В общем случае (a,b)≠(b,a), за исключением случая (a=b)
Прямым произведением двух множеств А и В, обозначаемым А× В, будем называть множество всех всевозможных упорядоченных пар, в которых на первое место выбирается всегда А, на второе В.
Бинарным отношением R из множества А в множество В будем определять как подмножество определенных упорядоченных пар из универсального множества пар:
Обратные
Дополнения отношения R
Тождественное отношение
Универсальное отношение
Композицией двух бинарных отношений R1⊂A �1 ⊂
� × � и �2 ⊂ � × � будем называть новое бинарное отношение R=R1°R2
ой степенью композиции R будем обозначать �� =
�°�°…°�°�
Свойства отношений: Пусть R задана на множестве А, тогда
R – называется рефлексивным, если
∀�∈�(�, �) ∈ � или ∃���, т.е. I⊂R
R – антирефлективный, если ∀�∈�(�, �) ∉
� или ¯∃¯�¯�¯�; � ∩ � = ∅
R - ни рефликтивный, ни антирефлективный, если есть хотя бы одна пара типа (a,a), но не все
R - Симметричное, если ∀�,�∈� �, � ∈
� => �, � ; � = �−1
R–антисимметричное, если ∀�,�∈� �, � ∈
� => �, � ∉ �; � ∩ �−1 ⊂ �
R - Ни симметричное, ни антисимметричное, если хотя бы 1 пара (a,b) есть перестановочный вариант, но не все.
R - Транзитивное, если ∀�,�,�∈� �, � ∈
�&(�, �) ∈ � => (�, �) ∈ �
R - Антитранзитивное, если неверно, что для любой тройки
¯∀¯¯¯¯¯¯¯¯�¯¯, ¯�¯¯∈¯¯¯�¯¯&¯¯(¯(¯�¯,¯�¯)¯¯∈¯¯�¯¯)¯=¯¯>¯¯(¯�¯¯, ¯�¯)¯∈¯¯¯
�,�,�∈�
Ни транзитивное, ни антитранзитивное, если есть хотя бы одно транзитивное замыкание, но не все ∃�,�,� �, � ∈
� &((�, �) ∈ �) => ((�, �) ∈ �)
Полное(линейное), если ∀�,�∈�((�, �) ∈
�)⋁(�, �) ∈ �
� ∪ � ∪ �−1 = � = � × � = �2
|
Функции: определения, инъекция, сюръекция, биекция. Композиция (суперпозиция или сложная функция), индуцированная функция.
Ответ: Функция �: � → �, для которого выполняется свойство ∀�∈�∃!�∈�(� � = �).
� : � → � называется инъекцией, если разные элементы множества X переводятся в разные элементы множества Y:
∀�1, �2 � � �1 ≠ �2 ⇒ (f x1 ≠ � �2 )
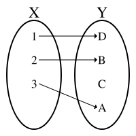
Отображение
называется сюръективным (или сюръекцией,
или отображением на), если ∀� ∈ � ∃� ∈ � � � = �
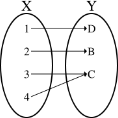
Отображение � : � → � называется биективным (или б иекцией), если оно инъективно и сюрьективно.
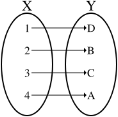
Композицией (суперпозиций или сложной функции) двух функций будет отображение �°�: � → �, где
�: � → �, �: � → �. � = � � � = � �
Теорема: Если � : � → � – функция, то
� : 2�л → 2�� и �−1 : 2�� → 2�� – тоже функция Замечание: F называется индуцированной функцией, а �−1 -переходам к прообразам.
|
 Скачать 134.15 Kb.
Скачать 134.15 Kb.