|
|
Множествами объединение, пересечение, разность и симметрическая разность, дополнение. Свойства операций и принцип двойственности правила
                      
Подстановки и их число. Группа подстановок и их графическое представление. Циклы и инверсии.
Ответ: Подстановкой из n символов (или подстановкой n-ой степени) называется любое взаимнооднозначное отображение множества этих символов на себя.
Существует n! различных подстановок n – ой степени.
Инверсией в
перестановке � называется всякая пара
индексов �, � такая, что
1 ≤ � < � ≤ � и � � > �[�].
|
Разбиения: числа Стирлинга и Белла.
Ответ: Числами Стирлинга первого рода (со знаком) �(�, �) называются коэффициенты многочлена:
�
� � = Σ � �, � ��
�=0
где � � — символ
Похгаммера (убывающий факториал):
� � = � � − 1 � − 2 …(� − � + 1)
В комбинаторике числом Белла �� называется число всех неупорядоченных разбиений n- элементного множества, при этом по определению полагают �0= 1.
|
Биномиальные коэффициенты и их свойства (бином Ньютона и треугольник Паскаля).
Ответ: Размещения – упорядоченные наборы. Сочетания – неупорядоченные наборы выбранных элементов.
Одной выборке (сочетанию) можно сопоставить путем перестановок выбранных элементов на m местах m! размещений, т.е. размещений в m! раз больше, чем сочетаний.
Т.е. для одной выборки (одного сочетания) m! размещений являются эквивалентными друг другу. Эти размещения образуют класс эквивалентности с мощностью m!
�� = �� = �!
�
� �! �−� !�!
Свойства сочетаний:
1. �� = ��−�
� �
2. �� - биномиальные коэффициенты
�
(� + �)� = �� + �0 + ���−1�1 + � � − 1 ∙ ��−2�2
+ ����−1 + �0��
�
= Σ �� ��−���
�
�=0
(� + �)3 = �0�3�0 + 3�2� + 3��2 + �3
3
�1 = �2
33 3 = � �� (a=b=1)
. 2� �=0 �
n=0 20 = 1 = �0 = 0! = 1 = 1
0 0!0! 1∙1
n=1 21 = 2 = �0 + �1 = 1 + 1 = 2
1 1
n=2 22 = 4 = �0 + �1 + �2 = 1 + 2 + 1 = 4
2 2 2
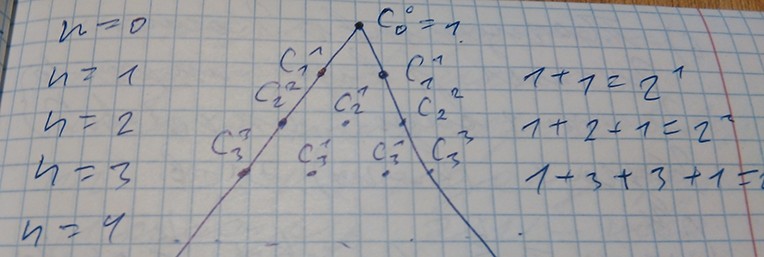
4. a = 1 (1 − 1)� = 0� = 0 = Σ� ( − 1)��� = 0
�=0 �
b = -1 lim �� = 1
�→0
5. �� = ��−1 + ��
� �−1 �−1
�! = � − 1 ! + � − 1 !
�! � − � ! � − 1 ! � − � ! �! � − � − 1
= (� − 1)! [� + � − �]
�! � − � !
= �!
�! � − � !
|
Принцип включения-исключения. Число булевых функций, существенно зависящих от всех своих переменных. Ответ: Принцип включений-исключений: Пусть у множеств А и В общая часть насчитывает k элементов. Тогда всего, в объединении множеств А и В, число элементов равно � + � − � т.е. � ∪
� = � + � − |� ∩ �|
Число различных булевых функций, зависящих от n переменных, равно 22�.
|
Производящие функции и метод неопределенных коэффициентов.
Ответ: Производящая функция последовательности �� - это формальный степенной ряд
Σ∞ ����.
�=0
Метод неопределенных
коэффициентов:
1)
Правую часть записанного равенства приводим к общему знаменателю, который совпадает со знаменателем дроби, стоящей в левой части этого равенства - ��(�), в числителе левой части получим некоторый многочлен ��(�) с неизвестными коэффициентами;
2)
Используем тот факт, что две дроби равны, когда равны их числители и знаменатели. Из того, что знаменатели левой и правой частей равенства равны, то значит, равны и числители:
�� � = �� �
3)
Два многочлена равны, если равны коэффициенты при соответствующих степенях переменной, поэтому приравниваем коэффициенты при одинаковых степенях переменной. В результате получаем систему для определения неизвестных коэффициентов.
|
Граф, псевдограф, мультиграф, подграф, надграф, частичный граф, нуль-граф.
Ответ: Граф – это множество V точек, определенным образом соединенных между собой линиями, необязательно прямыми.
Псевдограф – граф, содержащий петли или кратные ребра.
Мультиграф – псевдограф без петель. Подграф - граф, содержащий некое подмножество вершин данного графа и все рёбра, инцидентные данному подмножеству.
Добавим к графу G с n вершинами еще 1 вершину, соединенную какм-либо образом с вершинами графа. Новый граф с n+1 вершинами называется надграфом.
Частичный граф - граф, содержащий все вершины исходного графа и подмножество его рёбер.
Нуль-граф – граф, не содержащий рёбер.
|
Смежность. Инцидентность. Степень вершины. Однородный граф. Полный граф. Дополнение графа.
Ответ:
Смежность – понятие, используемое в отношении только двух рёбер либо только двух вершин.
Инцидентность – понятие, используемое только в отношении ребра или дуги и вершины: если v1, v2 вершины, а e=(v1, v2) — соединяющее их ребро, тогда вершина v1 и ребро e инцидентны, вершина v2 и ребро e тоже инцидентны. Две вершины (или два ребра) инцидентными быть не могут.
Степень вершины — количество рёбер графа G, инцидентных вершине x.
Обозначается �(�). Минимальная степень вершины графа G обозначается δ(G), а максимальная — △(G).
Однородный граф — граф, степени всех вершин которого равны, то есть каждая вершина имеет одинаковое количество соседей. Степень регулярности является инвариантом графа и обозначается.
Полный граф — простой неориентированный граф, в котором каждая пара различных вершин смежна. Дополнение графа — граф над тем же множеством вершин, что и исходный, но вершины соединены ребром тогда и только тогда, когда в исходном графе ребра нет.
|
Объединение и пересечение графов. Изоморфизм. Матрица смежности и матрица инциденций.
Ответ:
Объединением графов G1(V1, E1) и G2(V2, E2) называется граф G(V, E) =�1 ∪ �2 ,
где V = �1 ∪ �2, E = �1 ∪ �2 Пересечением графов G1(V1, E1) и G2(V2, E2) называется граф G(V, E) = �1 ∩ �2 ,
где V = �1 ∩ �2 E = �1 ∩ �2. Изоморфизм. Два графа называются изоморфными, если существует перестановка вершин, при которой они совпадают. Иначе говоря, два графа называются изоморфными, если существует взаимно-однозначное соответствие между их вершинами и рёбрами, которое сохраняет смежность и
инцидентность (графы отличаются только названиями своих вершин).
Матрица смежности – способ задания графов. Матрица смежности представляет собой квадратную таблицу размерами n⤫n, где n – число вершин графа.
Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).
| |
|
|
 Скачать 134.15 Kb.
Скачать 134.15 Kb.





















