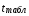Множественная линейная регрессия и корреляция
 Скачать 73.73 Kb. Скачать 73.73 Kb.
|
|
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Российский университет транспорта (МИИТ)» Институт экономики и финансов Кафедра «Математика» Кейс-задание №2 по дисциплине: «Эконометрика» на тему: «Множественная линейная регрессия и корреляция» Вариант __ Выполнил(а): студент(ка) группы _____ _________________________________ _________________________________ Проверил(а): Москва 20__ Условия задания Заданы значения зависимой переменной (Y) и пяти независимых переменных (X), характеризующих экономическую деятельность 53 предприятий. I. Корреляционный анализ 1.1. Построить корреляционную матрицу. 1.2. Проанализировать матрицу межфакторных корреляций. Выявить зависимые объясняющие переменные. Сделать выводы. 1.3. Проанализировать взаимосвязь зависимой и объясняющих переменных. Сделать выводы. 1.4. По результатам анализа (пункты 1.2, 1.3) выбрать две объясняющие переменные, наиболее тесно связанные с зависимой переменной. II. Регрессионный анализ 2.1. Построить уравнение множественной линейной регрессии по пяти объясняющим переменным. 2.2. Построить уравнение множественной линейной регрессии по двум объясняющим переменным, выбранным в пункте 1.4. Для него выполнить пункты 2.2.1 – 2.2.6. 2.2.1. Найти среднюю относительную ошибку аппроксимации. Сделать вывод. 2.2.2. Проверить критерии Фишера и Стъюдента. Найти интервальные оценки параметров уравнения регрессии. Сделать выводы. 2.2.3. Найти коэффициент детерминации. Поверить его статистическую значимость. Сделать выводы. 2.2.4. Найти коэффициент множественной корреляции. Сделать выводы. 2.2.5. Сделать вывод о качестве модели множественной линейной регрессии с двумя объясняющими переменными. 2.2.6. Для уравнения регрессии с двумя объясняющими переменными найти средние и частные коэффициенты эластичности. Оценить силу влияния объясняющих переменных на зависимую переменную. Сделать выводы. 2.3. Провести сравнительный анализ уравнений регрессии. Выбрать наилучшее уравнение регрессии. I. Корреляционный анализ 1.1. Построить корреляционную матрицу. Корреляционная матрица имеет вид
Элементы корреляционной матрицы найдены по формулам:
1.2. Проанализировать матрицу межфакторных корреляций. Выявить зависимые объясняющие переменные. Вывод: ___________________________________________________________________ ________________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ 1.3. Проанализировать взаимосвязь зависимой и объясняющих переменных. Вывод: ___________________________________________________________________ ----------------------------------------------------------------------------------------------------------- ------------------------------------------------------------------------------------------------------------- ------------------------------------------------------------------------------------------------------------ ----------------------------------------------------------------------------------------------------------- 1.4. По результатам анализа (пункты 1.2 и 1.3) выбрать две объясняющие переменные, наиболее тесно связанные с зависимой переменной. Вывод: объясняющие переменные Х и Х наиболее тесно связаны с зависимой переменной Y , потому, что Замечание. Чтобы сделать вывод по коэффициентам парной корреляции воспользуйтесь таблицей Чеддока
II. Регрессионный анализ 2.1. Построить уравнение множественной линейной регрессии по пяти объясняющим переменным. Уравнение множественной линейной регрессии с пятью независимыми переменными имеет вид 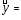 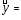 2.2. Построить уравнение множественной линейной регрессии по двум объясняющим переменным. Уравнение множественной линейной регрессии с двумя независимыми переменными имеет вид 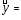 (записать уравнение в общем виде) (записать уравнение в общем виде)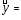 2.2.1. Найти среднюю относительную ошибку аппроксимации. Сделать вывод. Найдем среднюю относительную ошибку аппроксимации по формуле:
Вывод: ___________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ 2.2.2. Проверить критерии Фишера и Стъюдента. Сделать выводы. Проверим статистическую значимость уравнения регрессии в целом с помощью F-критерия Фишера. Расчетное значение критерия находится по формуле:
Найдем F-табличное: 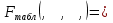 Вывод: ___________________________________________________________________ _______________________________________________________________________ Проверим статистическую значимость отдельных параметров уравнения регрессии с помощью критерия Стьюдента.
Найдем t-табличное: 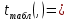 Вывод: ___________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ Найдем интервальные оценки параметров уравнения по формулам:
Вывод: ___________________________________________________________________ _______________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________ 2.2.3. Найти коэффициент детерминации. Поверить его статистическую значимость. Коэффициент детерминации находится по формуле:
Вывод: ___________________________________________________________________ _______________________________________________________________________ ________________________________________________________________________ Скорректированный коэффициент детерминации находится по формуле:
Оценим статистическую значимость коэффициента детерминации с помощью критерия Фишера. Найдем расчетное значение критерия по формуле:
Найдем F-табличное: 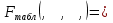 Вывод: ___________________________________________________________________ _______________________________________________________________________ 2.2.4. Найти коэффициент множественной корреляции. Простроить интервальную оценку с помощью z-преобразования Фишера. Сделать выводы. Коэффициент множественной корреляции по формуле:
Вывод: ___________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ Замечание. Чтобы сделать вывод по коэффициенту множественной корреляции воспользуйтесь таблицей
2.2.5. Сделать вывод о качестве модели множественной линейной регрессии с двумя объясняющими переменными. Вывод: ___________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ 2.2.7. Для уравнения регрессии с двумя объясняющими переменными найти средние и частные коэффициенты эластичности. Оценить силу влияния объясняющих переменных на зависимую переменную. Сделать выводы. Средние коэффициенты эластичности находятся по формуле:
Для уравнения множественной линейной регрессии с двумя переменными средние коэффициенты эластичности равны (формулы)
Средние коэффициенты эластичности
Вывод: ___________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ Уравнение множественной линейной регрессии с двумя переменными имеет вид 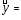 Для него найдены частные уравнения регрессии (формулы) Частные коэффициенты эластичности находятся по формулам
Вывод: ___________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ 2.3. Провести сравнительный анализ уравнений регрессии. Выбрать наилучшее уравнение регрессии.
Вывод: ___________________________________________________________________ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

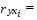
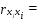
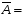
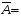
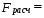
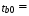
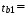
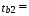
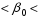
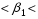
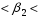
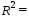
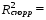
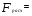
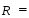
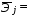
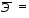
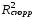
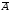
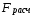
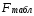
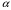
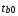
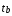 1
1