Множественная линейная регрессия и корреляция
 Скачать 166.11 Kb. Скачать 166.11 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Государственное образовательное учреждение высшего профессионального образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» Институт экономики и финансов Кафедра «Математика» Расчетно-аналитическая работа №3 по дисциплине: «Эконометрика» на тему: «Множественная линейная регрессия и корреляция» Вариант 12 Выполнила: студентка группы ЭБЭ-222 Патурян Нарек Проверила: Карпенко Н. В. Москва 2017 Условия задания Заданы значения зависимой переменной (Y) и пяти независимых переменных (X), характеризующих экономическую деятельность 53 предприятий. I. Корреляционный анализ 1.1. Построить корреляционную матрицу. 1.2. Проанализировать матрицу межфакторных корреляций. Выявить зависимые объясняющие переменные. Сделать выводы. 1.3. Проанализировать взаимосвязь зависимой и объясняющих переменных. Сделать выводы. 1.4. По результатам анализа (пункты 1.2, 1.3) выбрать две объясняющие переменные, наиболее тесно связанные с зависимой переменной. II. Регрессионный анализ 2.1. Построить уравнение множественной линейной регрессии по пяти объясняющим переменным. 2.2. Построить уравнение множественной линейной регрессии по двум объясняющим переменным, выбранным в пункте 1.4. Для него выполнить пункты 2.2.1 – 2.2.7. 2.2.1. Найти среднюю относительную ошибку аппроксимации. Сделать вывод. 2.2.2. Проверить критерии Фишера и Стъюдента. Найти интервальные оценки параметров уравнения регрессии. Сделать выводы. 2.2.3. Найти коэффициент детерминации. Поверить его статистическую значимость. Сделать выводы. 2.2.4. Найти коэффициент множественной корреляции. Простроить интервальную оценку с помощью z-преобразования Фишера. Сделать выводы. 2.2.5. Провести анализ остатков (проверить предпосылки МНК). 2.2.6. Сделать вывод о качестве модели множественной линейной регрессии с двумя объясняющими переменными. 2.2.7. Для уравнения регрессии с двумя объясняющими переменными найти средние и частные коэффициенты эластичности. Оценить силу влияния объясняющих переменных на зависимую переменную. Сделать выводы. 2.3. Провести сравнительный анализ уравнений регрессии. Выбрать наилучшее уравнение регрессии. I. Корреляционный анализ 1.1. Построить корреляционную матрицу. Корреляционная матрица имеет вид
Элементы корреляционной матрицы найдены по формулам:
1.2. Проанализировать матрицу межфакторных корреляций. Выявить зависимые объясняющие переменные. Вывод: Между факторами Х4 и Х15 существует средняя (умеренная) связь, т.к. для него абсолютное значение коэффициента парной корреляции соответственно равно 0,52 и попадает в интервал (0,5 - 0,7) шкалы Чеддока. Коррелированные факторы дублируют друг друга и одновременно не должны входить в уравнение регрессии. Между факторами Х4 и Х14, Х4 и Х7, Х4 и Х13, Х7 и Х14, Х7 и Х15, Х14 и Х15 связь слабая (абсолютные значения коэффициентов парной корреляции соответственно равны 0,49,0,35, 0,39, 0,44, 0,32 и 0,27, принадлежат интервалу (0,2; 0,5) шкалы Чеддока). Между факторами Х7 и Х13; Х13 и Х14, Х13 и Х15 связь практически отсутствует, т.к. для них абсолютные значения коэффициентов парной корреляции меньше 0,2. 1.3. Проанализировать взаимосвязь зависимой и объясняющих переменных. Вывод: Между объясняющими переменными Х15 и зависимой переменной Y1 связь отсутствует, т.к. для них абсолютные значения коэффициентов парной корреляции меньше 0,2. Между переменными X4, X7, X13, X14 и Y1 связь слабая, (абсолютное значение коэффициента парной корреляции равны 0,49, 0,20, 0,43, 0,23 принадлежат интервалу (0,2; 0,5) шкалы Чеддока). 1.4. По результатам анализа (пункты 1.2 и 1.3) выбрать две объясняющие переменные, наиболее тесно связанные с зависимой переменной. Вывод: объясняющие переменные Х и Х наиболее тесно связаны с зависимой переменной Y , потому, что Замечание. Чтобы сделать вывод по коэффициентам парной корреляции воспользуйтесь таблицей Чеддока.
II. Регрессионный анализ 2.1. Построить уравнение множественной линейной регрессии по пяти объясняющим переменным. Уравнение множественной линейной регрессии с пятью независимыми переменными имеет вид 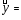 b0+b1*x4+b2*x7+b3*x13+b4*x14+b5*x15 b0+b1*x4+b2*x7+b3*x13+b4*x14+b5*x15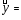 7,61+(-11,79)*x4+0,86*x7+0,0038*x13+0,01*x14+0,02*x15= 7,61+(-11,79)*x4+0,86*x7+0,0038*x13+0,01*x14+0,02*x15=2.2. Построить уравнение множественной линейной регрессии по двум объясняющим переменным. Уравнение множественной линейной регрессии с двумя независимыми переменными имеет вид 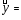 b0+b1*x4+b2*x13 b0+b1*x4+b2*x13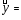 9,94+(-9,4)*x4+0,004*x13 9,94+(-9,4)*x4+0,004*x132.2.1. Найти среднюю относительную ошибку аппроксимации. Сделать вывод. Найдем среднюю относительную ошибку аппроксимации по формуле:
Вывод: так как 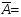 17,52% и находится в промежутке от 10 до 20, следует, что уравнение регрессии имеет хорошую точность. 17,52% и находится в промежутке от 10 до 20, следует, что уравнение регрессии имеет хорошую точность.2.2.2. Проверить критерии Фишера и Стъюдента. Сделать выводы. Проверим статистическую значимость уравнения регрессии в целом с помощью F-критерия Фишера. Расчетное значение критерия находится по формуле:
Найдем F-табличное: 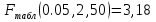 Вывод: так как Fрасч > Fтабл , то уравнение статистически значимо в целом. Проверим статистическую значимость отдельных параметров уравнения регрессии с помощью критерия Стьюдента.
Найдем t-табличное: 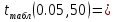 2,01 2,01Вывод: Оценки параметров b0 и b2 статистически значимы tb0 > t табл, tb2>t табл ; оценка параметра b1 - статистически не значима tb1 < t табл Найдем интервальные оценки параметров уравнения по формулам:
2.2.3. Найти коэффициент детерминации. Поверить его статистическую значимость. Коэффициент детерминации находится по формуле:
Вывод: Коэффициент детерминации показывает, что факторы Х4 и Х13 на 31% объясняют формирование значений показателя Y1. Скорректированный коэффициент детерминации находится по формуле:
Вывод: Х4 и Х13 на 28% объясняют формирование значений показателя «индекс снижения себестоимости продукции» Y1. Оценим статистическую значимость коэффициента детерминации с помощью критерия Фишера. Найдем расчетное значение критерия по формуле:
Найдем F-табличное: 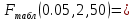 3,18 3,18Вывод: Если Fрасч > Fтабл, то уравнение статистически значимо в целом. 2.2.4. Найти коэффициент множественной корреляции. Простроить интервальную оценку с помощью z-преобразования Фишера. Сделать выводы. Коэффициент множественной корреляции по формуле:
Интервальная оценка (доверительный интервал) коэффициента множественной корреляции R находится с помощью z-преобразования Фишера 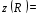 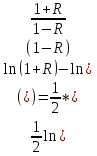 Предварительно устанавливается интервальная оценка для z в виде 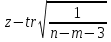 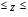 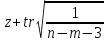 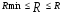 max maxВывод: Между факторами «Премии и вознаграждение на одного работника» и «Среднегодовая стоимость ОПФ» и показателем «Производительность труда» существует средняя множественная корреляционная зависимость. Замечание. Чтобы сделать вывод по коэффициенту множественной корреляции воспользуйтесь таблицей
2.2.5. Провести анализ остатков (проверить предпосылки МНК). Остатки найдем по формуле 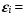 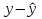 1. Проверим требованиe D теоремы Гаусса-Маркова. a) Среднее значение остатков равно:
Вывод: Математическое ожидание остатков (среднее арифметическое) равно 0, тогда первая часть требования теоремы Гаусса-Маркова считается выполненной б) На графике (рис.) точки внутри горизонтальной полосы, симметричной оси абсцисс. Рисунок. График остатков Вывод: На графике точки равномерно расположены внутри горизонтальной полосы, симметричной оси абсцисс, кроме 50 и 52 точки, которые выходят за рамки. Дисперсия остатков постоянна (остатки гомоскедастичны). Второе условие требования D выполняется. Точечная оценка дисперсии остатков 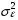 равна: равна:
Интервальная оценка дисперсии остатков находится по формуле: 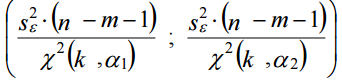 ; ; 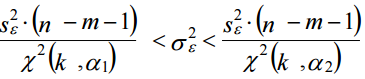  Критические значения распределения χ2 Пирсона найдем по числу степеней свободы df =50 и уровням значимости α1 =1 – α/2 =0,975 , α2 = α/2 =0,025
2. Проверим требование Е теоремы Гаусса-Маркова - для разных наблюдений остатки εi независимы. Воспользуемся критерием Дарбина-Уотсона. Вычислим статистику по формуле:
Для уравнения множественной линейной регрессии теоретические значения критерия Дарбина-Уотсона найдем по таблице критических значений, по объему выборки n=53, числу степеней свободы df=1 и уровню значимости α = 0,05.
Вывод: Поскольку dрасч=1,56 попадает в интервал (1,48:1,63), в котором автокорреляция остатков отсутствует, остатки независимы. Требование Е выполняется. 2.2.6. Сделать вывод о качестве модели множественной линейной регрессии с двумя объясняющими переменными. Вывод: Уравнение множественной линейной регрессии с двумя независимыми переменными имеет хорошую точность, статистически значимо в целом, однако не все параметры уравнения статистически значимы. Факторы на 28% объясняют ее значения. Уравнение имеет достаточно хорошее качество. 2.2.7. Для уравнения регрессии с двумя объясняющими переменными найти средние и частные коэффициенты эластичности. Оценить силу влияния объясняющих переменных на зависимую переменную. Сделать выводы. Средние коэффициенты эластичности находятся по формуле:
Для уравнения множественной линейной регрессии с двумя переменными средние коэффициенты эластичности равны (формулы)
Средние коэффициенты эластичности
Вывод: Средний коэффициент эластичности показывает, что при увеличении среднего значения фактора «трудоемкость единицы продукции» (Х4) на 1 единицу своего измерения среднее значение показателя «производительность труда» (Y1) уменьшится на 0,51%, при неизменности средне годового фонда заработной платы ППП (Х13). Средний коэффициент эластичности показывает, что при увеличении средне годового фонда заработной платы ППП (Х13) на 1 единицу своего измерения среднее значение показателя «производительность труда» (Y1) уменьшится на 0,011%, при неизменности трудоемкости единицы продукции (Х4). Уравнение множественной линейной регрессии с двумя переменными имеет вид  9,94+(-9,4)*x4+0,004*x13 9,94+(-9,4)*x4+0,004*x13Для него найдены частные уравнения регрессии (формулы) Частные коэффициенты эластичности находятся по формулам
Вывод: Частные коэффициенты эластичности показывают, что при неизменности среднегорного показателя фонда заработной платы ППП рост трудоемкость единицы продукции на 1 единицу своего измерения приводит к наибольшему росту производительности труда на предприятии 37. На предприятиях 25, 31, 46 – наименьший рост производительности труда. На предприятиях 7, 19, 41, 44, 47, 53 рост производительности такой же, как в среднем по группе предприятий. Частные коэффициенты эластичности показывают, что при неизменности трудоемкость единицы продукции рост среднегодового фонда заработной платы ППП труда на 1 единицу своего измерения приводит к наибольшему росту производительности труда на предприятии 14, 15. На предприятии 37 – наименьший рост производительности труда. На предприятиях 9, 16, 21, 40, 47 рост производительности такой же, как в среднем по группе предприятий. 2.3. Провести сравнительный анализ уравнений регрессии. Выбрать наилучшее уравнение регрессии.
Вывод: Наилучшим уравнением, наиболее адекватно описывающим исходные данные, является уравнение с 5 объясняющими переменными, так как в его случае скорректированный коэффициент детерминации имеет большее значение (0,28 > 0,21). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

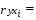
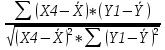 =-0,49
=-0,49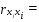
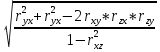
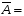
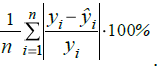
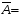 17,52%
17,52%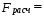
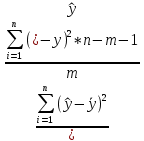
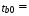
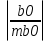 =7,77
=7,77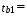
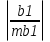 =2,98
=2,98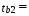
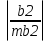 =2,24
=2,24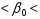 b0+mb0*tтабл
b0+mb0*tтабл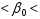 12,5
12,5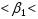 b1+mb1*tтабл
b1+mb1*tтабл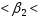 b2+mb2*tтабл
b2+mb2*tтабл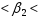 0,0072
0,0072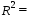
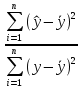
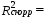
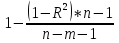
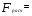
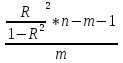
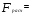 11,28
11,28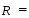
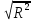
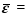
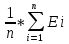 = 0
= 0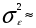
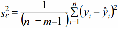
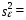 4,97
4,97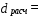
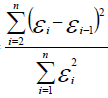
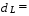 1,48
1,48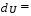 1,63
1,63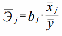
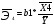
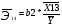
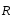
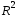
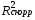
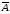
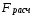
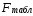
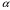
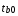
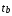 1
1