Моделирование финансовых процессов
 Скачать 0.86 Mb.
|
|
Простые проценты:    , т.к.  свойство 30 не выполняется.Сложные проценты:   ; свойство 30 выполняется.Таким образом, для финансовых платежей использование формулы простых процентов не рекомендуется т.к. результат зависит от периода времени приведения потоков платежей. Рассмотрим следующую задачу использования функций приведения. Задача: Пусть имеем два вклада: первый на период  доходной ставкой  , второй на период  доходной ставкой  . Какой из вкладов привлекателен для инвестирования?Решение: Возможны следующие варианты решения: 1) Определим  – интервал времени, к которому приводим и :из  находим  . Аналогично,  .Сравниваем  и  , и выбираем вклад с большим значением.В качестве в финансовых расчетах, как правило, берется один год.2) Приводим к периоду времени второго варианта вклада: .Сравниваем  и , и выбираем вклад с большим значением.2.2. Учет инфляции Чистая доля прибыли r при значении абсолютной валовой прибыли р, включающая инфляцию  , за тот же период определяется формулой  или  или  .Если   , то  , а при достаточно малых  ,  .2.3. Оценка потоков платежей При известной учетной ставке чистой прибыли за год, определение приведенных доходов Д, расходов Pнорму прибыли  на весь период реализации потока платежей и годовую норму прибыли ρгод по следующим формулам: ,  , ,  ,где  – величина дохода в момент времени t,  (при  – величина расхода в момент времени t),  – функция приведения к начальному (нулевому) периоду времени по сложным процентам,  – интервал осуществления платежей.В финансовом анализе время осуществления платежа имеет большое значение, так, при ежемесячных платежах важным является не только процентная ставка, а также в какой день месяца будет осуществляться платеж (в начале месяца или в конце). Определение выгод от технологии организации платежей (финансовых потоков) являются задачами специальных дисциплин. 2.4. Задание для самостоятельного выполнения По данным значениям годовой доли общей прибыли  и инфляции : 1. Определить коэффициенты приведения к периодам  ,  ,  ,  по простым и сложным процентам.2. Определить норму годовой чистой прибыли (без инфляции) –  .3. Для платежей  , осуществляемых в моменты времени  , определить приведенную норму чистой годовой прибыли.Данные для вариантов приведены в таблицах 7 и 8. Таблица 7
Таблица 8
3. УПРАВЛЕНИЕ ФИНАНСОВЫМИ РИСКАМИ Одним из инструментов понижения рисков финансовых операций является диверсификация (смешение, взаимное проникновение) операций. Рассмотрим это на примере операций с банковскими активами. Состояние активов банка необходимо оценивать с учетом их надежности, т.е. вероятности возврата кредитов. При этом следует учесть уровень надежности (риска), сумму кредита  , срок возврата кредита.Сумма «кредитных» активов банка может быть оценена по следующей формуле:  где  – вероятность того, что i-й кредит невозвратен ( ); – функция приведения суммы кредита к расчетному моменту времени, например,  , – коэффициент дисконтирования.3.1. Определение портфеля кредитов с минимальным риском Для минимизации риска банковских операций необходимо производить их хеджирование, то есть смешение с целью уменьшения риска. Как известно, производится хеджирование слабокоррелированных (или отрицательно коррелированных) финансовых операций с одинаковым сроком исполнения или сильнокоррелированных финансовых операций с разным сроком исполнения. Так, фьючерсные контракты (финансовые операции) могут хеджироваться с короткими контрактами (финансовыми операциями) одной и той же формы; операции с ценными бумагами могут хеджироваться с предоставлением кредитов предприятиям и частным лицам и т.д. Пусть  – среднее квадратичное отклонение случайной величины – возврата средств по кредиту i-го вида,  – средний процент возврата по i- му кредиту; – доля кредитов i-го вида в активах банка; – коэффициент корреляции кредитов i-го вида и j-го вида.Тогда среднее квадратичное отклонение возвратности портфеля кредитов  определяется  или, т.к.  и  , .Минимизация рисков портфеля кредитов может быть сформулирована как оптимизационная задача. Пусть определено по статическим данным для n видов кредитов среднее квадратичное отклонение возврата кредитов  , i = 1, 2, ..., n. Определить долю каждого вида кредита  в портфеле кредитов, так чтобы  , (1)при ограничениях  , (2) , i=1,2…,n , (3)где  .Решение задачи (1)-(3) (задача квадратичного программирования) дает относительные объемы средств, направленных на кредитование i-го вида финансовых операций, доставляющие минимум среднеквадратического отклонения от средней доходности портфеля, т.е. минимальные риски для портфеля операций. Если К – общий объем кредитов, то для минимизации риска следует направлять wiK средств на i-й вид кредитования. Заметим, что задача (1) - (3) имеет смысл в случае «относительно равной доходности кредитов». В более общем случае, когда каждый вид кредитования имеет свой процент доходности  – процент доходности i-го вида кредита ( ), задача (1)-(3) может быть сформулирована как двухкритериальная (многокритериальная). , (4) , (5)при ограничениях  , (6) , i=1,…,n . (7)Ограничение (6) имеет вид ограничения (3) и отличается только заменой равенства на неравенство, т.е. допускается использование не всей суммы К для кредитования. Задача (5)-(7) относится к задачам нелинейного программирования. Для численного решения оптимизационной задачи (1)-(3) (см. также (5)-(7)) можно использовать метод множителей Лагранжа. Функция Лагранжа имеет вид 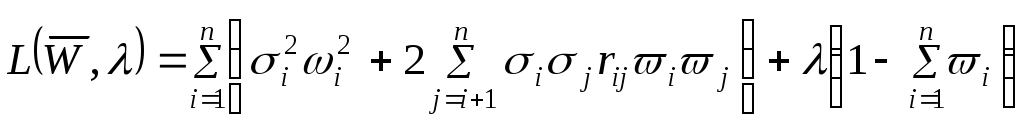 . (8)Найдем стационарные точки 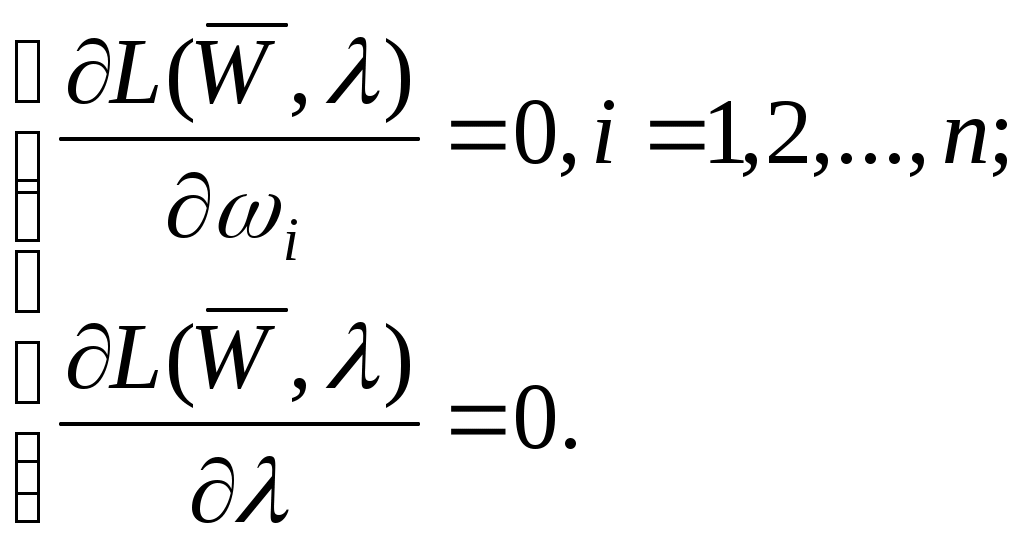 из решения системы уравнений: (9)Система (9) имеет следующий вид 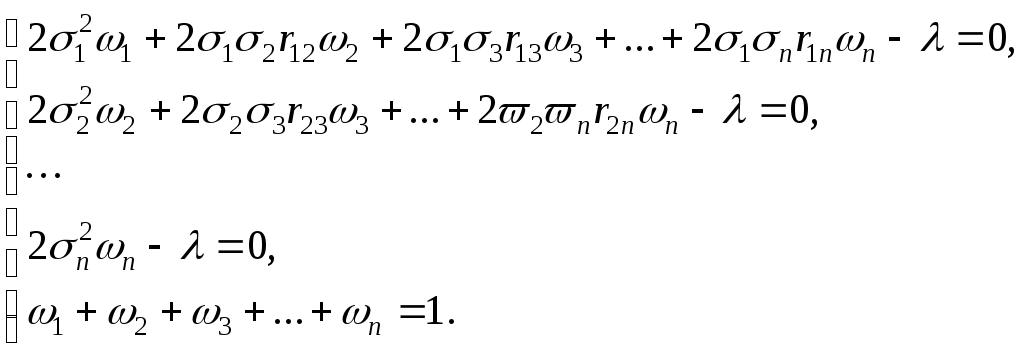 (10)Решение системы (10) ( (n+1) – уравнение и n+1 – переменных) является оптимальным, если выполняется условие 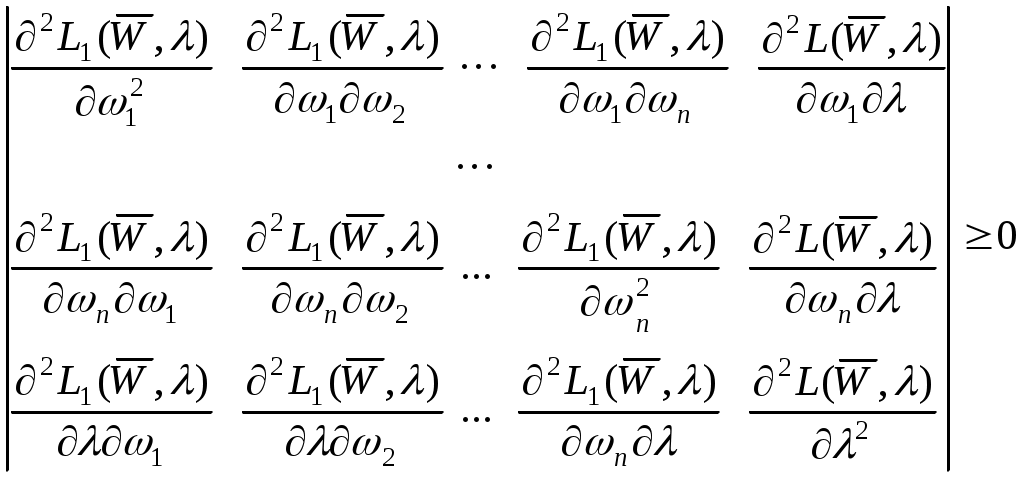 . (11)Нетрудно проверить выполнение условия (11). Задача (4)-(7) относится к классу многокритериальных задач, решение которых зависит от субъективных (экспертных) предпочтений. В общем случае задача сводится к нахождению оптимального («наилучшего») решения из множества Парето. Множество таких решений исходной многокрительной задачи, где для любого решения не существует другого решения, значения критериев на котором лучше, чем у первого. К одним из методов нахождения оптимального решения из множества Парето относится метод последовательных уступок. Вариант этого метода для задачи (4)-(7): 1.Определяем решение задачи (5)-(7). Пусть  – оптимальное значение риска.2. Определяем  – допустимая уступка ухудшения риска портфеля операций.3. Решаем задачу (4), (6)-(7), включив дополнительное ограничение:  . (12)Полученное решение является решением задачи (4)-(7) с субъективным параметром .3.2. Задание для самостоятельного выполнения Для двух видов кредитных операций по банку «Север» и банку «Юг» (таблицы 9 и 10) определить: 1. Среднее значение доходности по операции. 2. Среднее квадратичное отклонение доходности. 3. Коэффициент корреляции между операциями. 4. Средневзвешенный риск портфеля, считая что, равные доли средств направлены на каждую операцию. 5. Оптимальное распределение средств в объеме 10000 ед., доставляющее минимум риска портфеля – .6. Оптимальное распределение средств для получения максимальной прибыли при  =0,96+0.01H ,  =0,99-0,01H (где Н – номер варианта), при уровне риска портфеля не ниже  , где – оптимальный риск, вычисленный в пункте 5.7. Определить, какая из операций банка «Юг» предпочтительна для хеджирования с операцией банка «Север» (определенной по вашему варианту). Таблица 9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||