Моделирование финансовых процессов

• Название: Моделирование финансовых процессов
• Дата: 03.12.2021
• Размер: 0.86 Mb.
• Имя файла: modelir_finans_processov.doc
• Тип: Методические указания; #289993
• страница: 1 из 4

РОСЖЕЛДОР

Государственное образовательное учреждение

высшего профессионального образования

«Ростовский государственный университет путей сообщения»

(РГУПС)


Э.А. Мамаев, Б.А. Мамаева
МОДЕЛИРОВАНИЕ ФИНАНСОВЫХ ПРОЦЕССОВ
Методические указания


Ростов-на-Дону

2004



УДК 681.3.06

Э.А. Мамаев, Б.А. Мамаева

Моделирование финансовых процессов. - Ростов н/Д: Рост. гос. ун-т путей сообщения, 2004. - 32 с.

Предлагаются теоретические сведения и задания для самостоятельного выполнения по использованию математических моделей и методов в анализе финансовых процессов. Предназначена для студентов экономических специальностей.

Ил. 6. Табл. 14. Библиогр.: 6 назв.

Рецензенты: докт. экон. наук, проф. Ф.Б. Риполь-Сарагоси (РГУПС); канд. физ.- мат. наук, доц. С.А. Рухленко (РГУПС)

Мамаев Энвер Агапашаевич

Мамаева Бурлият Абдулгамидовна

Моделирование финансовых потоков

Методические указания

Редактор А.И. Гончаров

Техническое редактирование и корректура А.И. Гончаров

Подписано в печать 28.12.2004 г. Формат 60 х 84/16.

Бумага газетная. Ризография. Усл. печ. л. 1,86

Уч.-изд. л. 1,77. Тираж 60. Изд. № 188. Заказ № .

Ростовский государственный университет путей сообщения.

Ризография РГУПС

Адрес университета: 344038, Ростов н/Д, пл. Народного ополчения, 2.
© Ростовский государственный университет путей сообщения, 2004



СОДЕРЖАНИЕ
Введение

1. Детерминированные модели распределения ресурсов

1.1. Метод динамического программирования

1.1.1. Задача о распределении ресурсов

1.1.2. Задание для самостоятельного выполнения

1.2. Метод ветвей и границ

1.2.1. Оптимальный портфель инвестиций

1.2.2. Задание для самостоятельного выполнения

2. Фактор времени в моделировании финансовых потоков

2.1. Функции приведения

2.2. Учет инфляции

2.3. Оценка потоков платежей

2.4. Задание для самостоятельного выполнения

3. Управление финансовыми рисками

3.1. Определение портфеля кредитов с минимальным риском

3.2. Задание для самостоятельного выполнения

4. Динамические стохастические модели управления рисками финансовых операций

4.1. Биномиальные модели управления опционами

4.2. Задание для самостоятельного выполнения

5. Управления рисками финансовых операций. Метод Монте-Карло

5.1. Общая схема метода Монте-Карло

5.2. Задание для самостоятельного выполнения

Рекомендуемая литература



ВВЕДЕНИЕ
Финансовые потоки и процессы являются одними из динамичных областей исследований в экономике и финансах любой сферы бизнеса. Непрерывность, неопределенность (стохастика), подверженность рискам принятых решений – факторы, определяющие трудоемкость методического аппарата исследования финансовых потоков. В работе представлен математический инструментарий решения некоторых задач в этой области, приводятся задания для самостоятельного решения.

Статические модели распределения ресурсов предприятия с целью максимизации эффекта (дохода) представлены в постановках для решения методом динамического программирования (задача о распределении ресурсов) и методом ветвей и границ (задача об оптимальном портфеле инвестиций).

В динамических задачах управления финансовыми потоками определенную сложность представляет фактор времени и его учет в оценке разновременных платежей. Рассматриваются функции приведения платежей (сложные и простые проценты) и их использование в финансовых расчетах.

Неопределенность в реализации финансовых потоков рассматривается в теории финансовых рисков. Задачи минимизации рисков, оптимизации финансовых операций (портфеля) в условиях рисков связаны с элементами теории вероятности и статистического моделирования. Статистическое моделирование (метод Монте-Карло) используется в задачах управления опционами.
1. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ
1.1. Метод динамического программирования
Динамическое программирование (ДП) – это раздел математического программирования, определяющий совокупность приемов для нахождения оптимальных решений многошаговых (многоэтапных) процессов и основанный на вычислении последствий решения каждого шага по выработке оптимальной стратегии для последующих шагов. Процессы принятия решений, которые строятся по такому принципу, называются многошаговыми.

Рассмотрим управляемую систему, которая под влиянием управления переходит из начального состояния 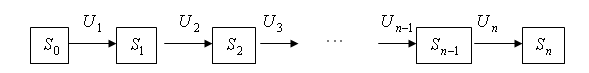в конечное . Предположим, что процесс управления системой может быть разбит на n шагов .

Пусть , … – состояние системы соответственно после 1-го, 2-го … n – го шага. Последовательное преобразование системы (по шагам) достигается с помощью некоторых мероприятий , … , которые определяют управление системой. ( – управление на k-м шаге, переводящее систему из состояния в ) (рис. 1).

Рис. 1
Управление на k-м шаге заключается в выборе значения определенной управляющей переменной.

Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом, т.е. любое неоптимальное решение на каком-либо шаге приводит к неоптимальным решениям, содержащим этот шаг. Предполагаем впредь, что состояние системы в конце к-гошага зависит только от предшествующего состояния системы и управления на данном шаге, т.е. ) – уравнение состояния.

Для применения метода ДП должны быть удовлетворены следующие условия:

1. Задача может быть интерпретирована как n-шаговый процесс управления, а показатель эффективности процесса может быть представлен в аддитивной форме, т.е. как сумма показателей эффективности на каждом шаге.

2. Структура задачи инвариантна относительно числа шагов n.

3. На каждом шаге состояние системы определяется параметрами состояния и управления, которые не зависят от числа шагов.

4. Выбор управления на k-м шаге есть функция, зависящая от предшествующего состояния и выбранного управления.

Порядок построения модели ДП и решения задачи методом ДП:

1. Выбрать способ деления на шаги.

2. Ввести параметры состояния и переменные управления на каждом шаге процесса.

3. Записать уравнение состояний.

4. Ввести показатели эффективности на k-м шаге и суммарный показатель – целевую функцию
.
5. Из ограничений задачи определить для каждого k-го шага – множество допустимых управлений на этом шаге.

6. Записать основное для вычислительной схемы ДП функциональное уравнение Беллмана
.
7. Приступить к вычислительной процедуре, включающий этапы условной и безусловной оптимизации.

Первый этап. Условная оптимизация для k-го шага

- записать уравнение Беллмана;

- определить уравнение состояния ;

- построить вспомогательную таблицу для хранения промежуточных результатов;

- результаты занести в основную таблицу.

Перейти ко второму этапу.

Второй этап. Безусловная оптимизация. Обеспечивает нахождение оптимальных управлений каждого шага обратным (к первому этапу) ходом вычислений, т.е. если допустить, что – оптимальное управление первого шага, то из уравнения находим . Находим – оптимальное управление второго шага и из уравнения находим . Аналогично расчеты продолжаем до n-го шага.
1.1.1. Задача о распределении ресурсов
Экономическая постановка. Планируется распределение средств ед. между n предприятиями (пусть ед. и ). Средства выделяются в размерах, кратных 40 ед.) Предполагается, что выделенные предприятию в начале планового периода средства приносят доход .

Будем считать, что

• 
  доход, полученный от вложения средств в предприятие, не зависит от вложения средств в другие предприятия;
  
• 
  доход, полученный от разных предприятий, выражается в одинаковых единицах;
  
• 
  общий доход равен сумме доходов, полученных от распределения средств по всем предприятиям.
  

Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарный доход был максимальным.

Математическая модель. Общий доход выражается целевой функцией
.
Переменные должны удовлетворять условию
, , .
Требуется определить переменные , которые удовлетворяют ограничениям и максимизируют целевую функцию.

Построение модели ДП

1. В качестве очередного шага будем рассматривать выделение средств -му предприятию (в размерах, кратных 40 ед.). Будем рассматривать предприятия последовательно, начиная с 3-го шага (предприятия).

2. В качестве состояния рассматриваем объем распределяемых средств на -м шаге, а в качестве управления рассмотрим объем распределяемых средств на -е предприятие, т.е. , ед. –начальное состояние.

3. Уравнение состояния .

4. Целевая функция имеет вид .

5. Множество допустимых управлений на -м шаге (множество ) задается неравенством , .

6. Уравнение Беллмана
.
Рассмотрим решение задачи при значениях функций , заданных в следующей табл.1
Таблица 1

0	0	0	0
40	8	6	3
80	10	9	4
120	11	11	7
160	18	13	11

Первый этап

Очевидно, при имеем и .

1. Рассмотрим ШАГ 3, . Тогда
.
Результаты расчетов представлены в табл. 2 (графы 1-6).

Для хранения окончательных результатов расчетов каждого шага используем табл. 3.

1. Рассмотрим ШАГ 2. . Уравнение Беллмана имеет вид
.

Таблица 2

		Итерации метода динамического программирования
			к=3,			к=2			к=1
1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	0	0	0	0	0	0	0	0	0
40	0	40	0	0	3	0	3	6	0	6	8
	40	0	3	3		6	6		8	8
80	0	80	0	0	4	0	4	9	0	9	14
	40	40	3	3		6	9		8	14
	80	0	4	4		9	9		10	10
120	0	120	0	0	7	0	7	12	0	12	17
	40	80	3	3		6	10		8	17
	80	40	4	4		9	12		10	16
	120	0	7	7		11	11		11	11
160	0	160	0	0	11	0	11	14	0	14	20
	40	120	3	3		6	13		8	20
	80	80	4	4		9	13		10	19
	120	40	7	7		11	14		11	17
	160	0	11	11		13	13		18	18

Результаты расчетов приведены в табл. 2 (графы 1-3, 7-9).

2. Рассмотрим ШАГ 3, . Уравнение Беллмана имеет вид
.
Результаты расчетов приведены в табл. 2 (графы 1-3, 10-12).
Таблица 3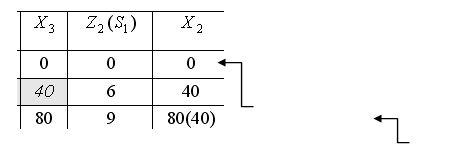


Таким образом, максимальный доход от распределения 160 ед. средств равен 20 (по табл. 3 или табл. 2 ).
Второй этап

Для определения оптимального распределения средств между предприятиями рассмотрим второй этап решения задачи.

Из табл.3 видно (см. выделенные ячейки, переходы указаны стрелками), что при , из находим ед. – средства распределяемые на предприятия 2 и 3.

Далее из табл. 3 при имеем при ед.

И, наконец, ед. ед.

Таким образом, для получения максимального дохода в объеме 20 ед. необходимо распределить 40 ед. средств в первое предприятие, 80 ед. – во второе и 40 ед. – в третье предприятие.

Заметим, что для проведения расчетов достаточно хранить информацию из табл. 1,3, а табл. 2 является вспомогательным, и результаты каждой итерации могут не храниться в памяти.
1.1.2. Задание для самостоятельного выполнения
Распределить средства ед. (Н=1,2,3, … – номер варианта) между предприятиями так, чтобы суммарный доход был максимальным, если известно, что выделенные предприятию в начале планового периода средства приносят доход , . Данные для расчетов приведены в табл. 4
Таблица4

X	f1(X)	f2(X)	f3(X)	f4(X)	f5(X)
0	0	0	0	0	0
25H	80-2H	60	30+H	20+2Н	70
50H	100	90-Н	45+H	120	135-2H
75H	110	110	70	140	145-H
100H	180-2H	130-Н	110	160+Н	150

1.2. Метод ветвей и границ
Для решения задач на дискретном множестве решений часто используется метод ветвей и границ, алгоритм которого приведем для задачи в общем виде:

,

.

Определим следующие процедуры и правила:

1. Правило R– разбиение множества любого решений на подмножества:
.
2. Множество подмножеств решений .

3. Функция верхней оценки целевой функции на множестве решений , обозначаемая , которая удовлетворяет условиям для всех , и для всех .

4. Правило выбора из подмножества подмножества для последующего разбиения – , т.е. .

5. Рекордное (текущее лучшее) решение и .

Идея метода ветвей и границ заключается в последовательном разбиении исходной задачи на подзадачи (ветвление) и поиске решения этих задач. При этом для сокращения полного перебора решений используются оценки целевой функции для подзадач (границы). В процессе решения производится исключение подзадач из рассмотрения (элиминация), если их оценка «хуже» (меньше для задачи на поиск max), чем значение целевой функции для текущего лучшего решения – рекорда . В общем виде алгоритм ветвей и границ имеет следующий вид.
Вход: Определим .
Шаг 1. Выбираем подмножество для разбиения и производим разбиение этого множества, т.е. . Изменим множество : .
Шаг 2. Определим для каждого подмножества значение , если , и , если (множество включает только один элемент).
Шаг 3. Для всех выполним:
- если и , то и ;
- .
Шаг 4. Для всех выполним .
Шаг 5. Если , то переходим на Шаг 1.
Выход: – оптимальное решение, – оптимальное значение целевой функции.
1.2.1. Оптимальный портфель инвестиций
Пусть требуется распределить ресурсов для реализации проектов, если известно – объем ресурса для реализации -го проекта, – эффект от реализации -го проекта, .

Обозначим

Требуется найти оптимальное распределение ресурса между проектами, т.е.

при ограничении
.
Рассмотрим пример реализации метода ветвей и границ для этой задачи при следующих исходных данных: 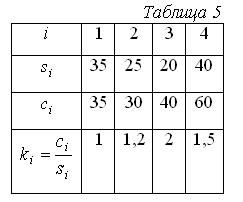, данные и представлены в табл. 5. Упорядочим проекты в порядке убывания , которые приведены в табл. 5

Упорядоченные проекты в порядке убывания эффекта на единицу ресурса представлены в табл. 6.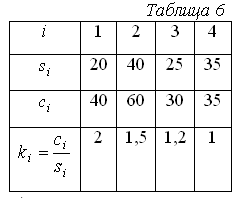

Определим правило разбиения множества решений
по некоторой переменной,
например : , и ,
т.е. в включены все решения, в которых , а в включены все решения, в которых , Для разбиения будем выбирать переменные из табл. 6 последовательно слева направо.

Определим верхнюю оценку целевой функции на множестве

с определенными 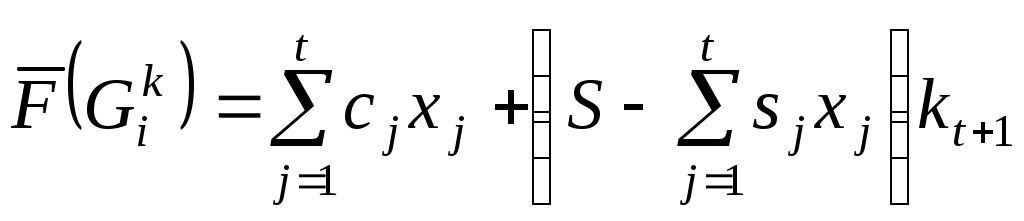первыми компонентами:
, где .
В качестве правила – выбора очередного подмножества для разбиения – примем выбор подмножества с максимальной верхней границей.

Реализация метода ветвей и границ для данной задачи в графической форме приведена на рис. 2.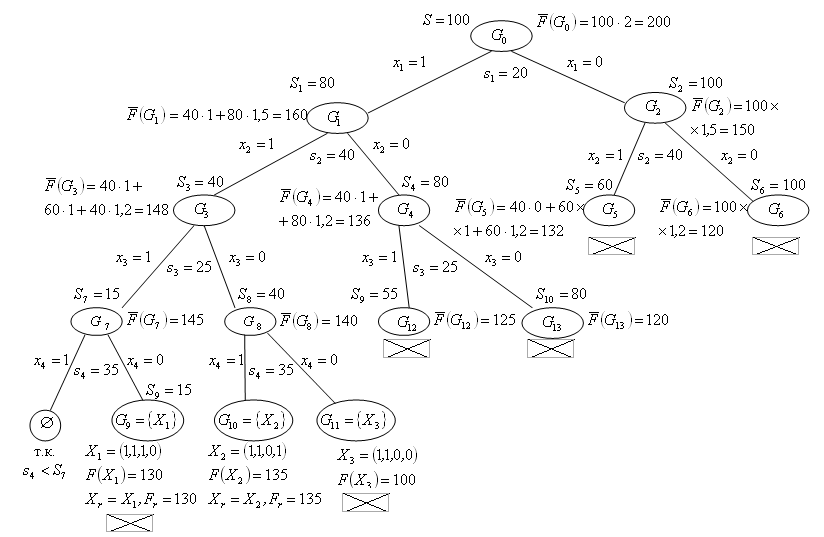


Рис.2
Н а рис. 2 через 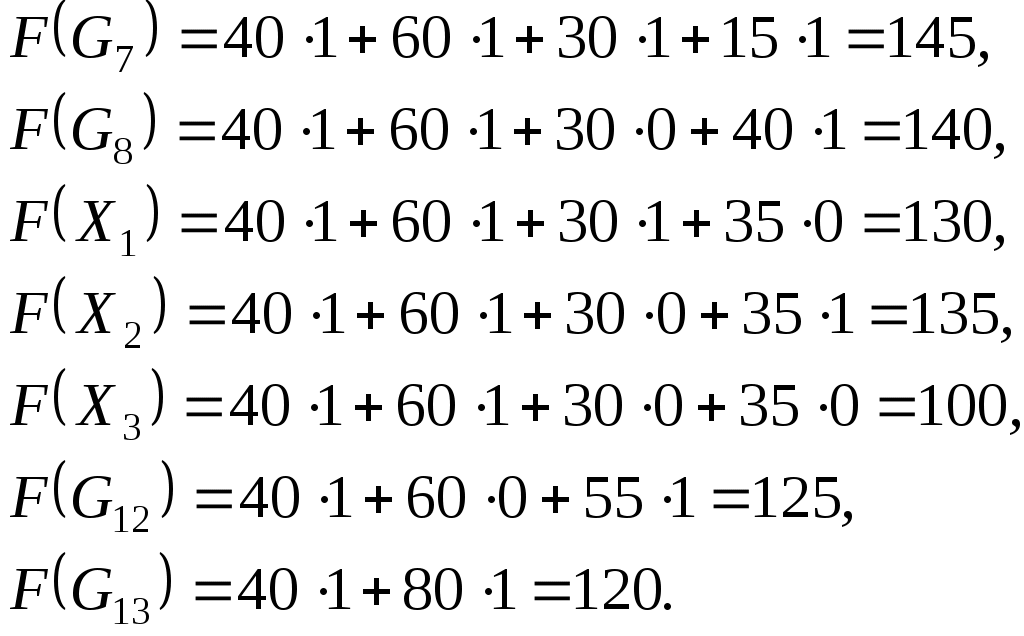обозначен «нераспределенный» ресурс для множества . Приведем в развернутом виде расчеты оценок и значений целевой функции для вершин (подмножеств):

Последовательность выбора и разбиения подмножеств решений определена их порядком, первое рекордное решение позволило исключить из рассмотрения подмножества , т.к. его оценка меньше, чем . Дальнейшее разбиение подмножества позволяет получить новое рекордное решение с , которое позволяет исключить все остальные подмножества.

Таким образом, оптимальное решение: , т. е. средства распределяются в проекты 1,2,4 или 2, 3, 4 в исходной нумерации.
1.2.2. Задание для самостоятельного выполнения
Определить оптимальный портфель инвестиций по величине заданного ресурса S=1000+20Н (Н-номер варианта) из шести проектов. Данные о потребности ресурсов проектов ( 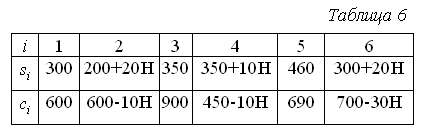) и эффектов от проектов ( ) представлены в табл. 6.

2. ФАКТОР ВРЕМЕНИ В МОДЕЛИРОВАНИИ ФИНАНСОВЫХ ПОТОКОВ
На финансовом рынке используются два понятия, связанные с учетом фактора времени в расчетах:

- дисконтирование – приведение будущих платежей к текущему периоду;

- наращивание – приведение текущих платежей к будущему периоду.

Для операций наращивания и дисконтирования используются функции приведения ( , ), где

– базисный период времени, к которому приводятся платежи;

– период осуществления платежей.
2.1. Функции приведения
Функции приведения должны удовлетворять следующим свойствам:

1⁰. ( , ) = 1;
2⁰_. ( , ) = , ( ,) = 0;
3⁰_. .
Часто функция приведения ( , ) записывается без , т.е. ( , )= , а – оговаривается по тексту.

Распространенными функциями приведения являются:
1. Функция простых процентов: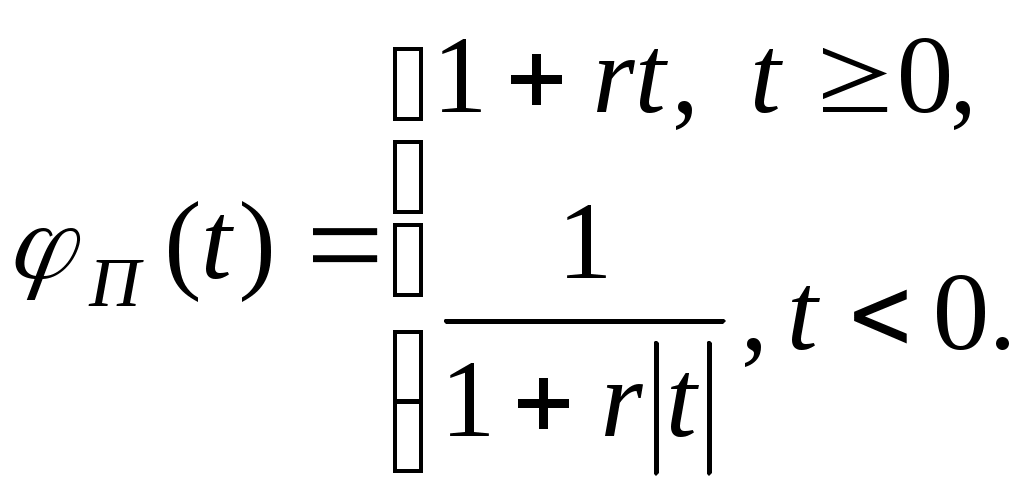

Функция сложных процентов: .

Несложно проверить, что свойства 1⁰ – 2⁰ для и выполняются, а свойство 3⁰ для простых процентов не выполняется (рис. 3).


Рис.3