Моделирование финансовых процессов
 Скачать 0.86 Mb.
|
|
4. ДИНАМИЧЕСКИЕ СТОХАСТИЧЕСКИЕ МОДЕЛИ УПРАВЛЕНИЯ РИСКАМИ ФИНАНСОВЫХ ОПЕРАЦИЙ 4.1. Биномиальные модели управления опционами Как известно, распределение дискретной случайной величины в n независимых испытаниях с двумя исходами («да», «нет») с одинаковой вероятностью исходов во всех испытаниях называют биномиальным распределением. В качестве исходов можно в финансовом анализе рассматривать увеличение и уменьшение цены активов на определенную величину за фиксированный интервал времени. Разбивая временной период на n дискретных одинаковых периодов и считая независимыми изменения цены активов, получаем цену актива как случайную величину с биномиальным распределением. Пусть p – вероятность повышения цены актива за один интервал времени. Тогда вероятность m увеличений цены актива за n интервалов времени равно  ,где  – число вариантов достижения m успехов при n попытках,  – факториал.Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины равны:  ,  ,  .Биномиальное дерево цен активов. Пусть за один интервал времени цена активов S может увеличиваться в u раз с вероятностью p иуменьшаться в d раз с вероятностью 1-p. Биномиальное дерево цен активов за 2 два интервала времени будет иметь вид, представленный на рис. 4. 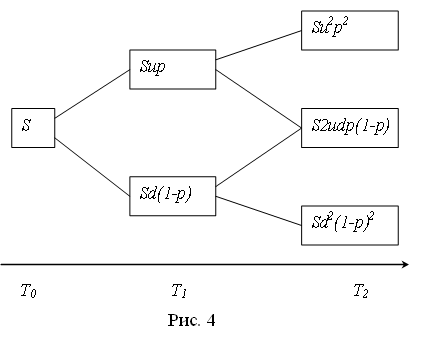 Биноминальное дерево используется в исследованиях ценообразования опционов. Опцион представляет собой контракт, заключаемый между двумя инвесторами, один из которых продает (выписывает) опцион, а другой покупает его и приобретает тем самым право (но не обязанность) в течение оговоренного в условиях опциона срока либо купить, либо продать по фиксированной цене определенное количество или значение конкретного базисного актива. В качестве базисного актива опциона могут фигурировать занесенные в биржевой список обыкновенные акции, иностранная валюта, фондовые индексы, краткосрочные депозиты, государственные облигации, фьючерсные контракты. Опцион купли (call) – соглашение на право покупки ценных бумаг в течение определенного времени по установленной цене. Опцион продажи (put) – соглашение на право продать ценные бумаги в течение определенного времени по установленной цене. К задачам управления опционами относится определение сроков и объемов операций с опционами, минимизируя связанные с активами риски. Биномиальная модель решает задачу создания безрискового портфеля посредством хеджирования длинной позиции по активу короткой позицией по ряду справедливо оцененных опционов по покупке этого актива. 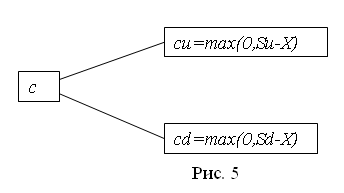 Пусть S – цена основного актива; X – цена исполнения опциона; r – безрисковая процентная став-ка (доля), R=1+r; u – коэффициент движения цены вверх; d – коэффициент движения цены вниз. Тогда за один интервал времени имеем (см. рис. 5):  – цена продажи опциона (стоимость при повышении цены); – цена приобретения опциона (стоимость при понижении цены).с –стоимость опциона. 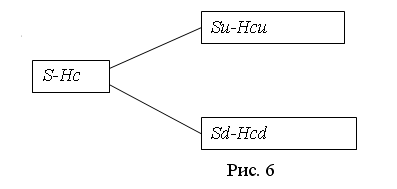 Пусть для построения полностью захеджированного опциона покупается единица актива и про-дается H опционов (рис.6). Тогда из условия Su-Hcu= Su-Hcd находим H, т.е.  .Справедливая цена продажи опционов: из условия  определяется .4.2. Задание для самостоятельного выполнения 1. Ценная бумага может подорожать в u раз в течение следующего месяца с вероятностью p1 или подешеветь в прочих условиях. Предполагая, что ежемесячные изменения цены независимы, рассчитать: 1.1 Вероятность того, что за 2 месяца цена станет больше w1S, где S – первоначальная цена. 1.2. Вероятность того, что за 3 месяца цена станет меньше w2S. 1.3. Вероятность того, что ценная бумага через год будет стоить больше w3S. 2. Определить параметры управления опционами: 2.1. Количество опционов, которое следует продать для полностью захеджированного портфеля. 2.2. Определить справедливую цену опциона. Значения параметров задания для вариантов приводятся в табл. 11 и 12. Таблица 11
Таблица 12
5. УПРАВЛЕНИЯ РИСКАМИ ФИНАНСОВЫХ ОПЕРАЦИЙ. МЕТОД МОНТЕ-КАРЛО 5.1. Общая схема метода Монте-Карло Процесс исследования финансовых рисков на основе метода Монте–Карло, статистического имитационного метода, включает следующие этапы: 1. Определение стохастической природы объекта исследования, т.е. - определение теоретических законов распределения случайных величин, статистическое исследование случайных процессов; - подтверждение гипотез о теоретических законах распределения случайных величин. 2. Имитация движения входных переменных с помощью многократного генерирования случайных чисел, корректируемых с таким расчетом, чтобы иметь такое же распределение вероятностей, как и основная переменная. Это подразумевает преобразование случайных чисел с равномерным распределением, сгенерированных компьютером, в случайные переменные с таким же распределением, что и переменные, предназначенные для моделирования. Скорректированные случайные переменные являются входными переменными. 3. Осуществление моделирования – объединение входных переменных вместе в соответствии с логикой системы, описывающей, каким образом связаны входные переменные и как получаются выходные. С помощью многократного генерирования случайных чисел мы получаем будущее значение искомой переменной. 4. Многократное повторение этого процесса позволяет найти среднюю полученных значений. Эта средняя – будущее (ожидаемое) значение моделируемой переменной. Затем для определения настоящей стоимости моделируемой переменной это будущее значение дисконтируется по соответствующей дисконтной ставке. 5. Применение техники контроля разбросанности – определение стохастической природы объекта исследования на основе полученной имитацией статистики о поведении процесса. 5.2. Задание для самостоятельного выполнения На основе статистических исследований методом Монте-Карло для биномиальной модели управления опционами определить: 1. Вероятность того, что за n дней цена опциона станет выше w1 S. 2. Вероятность того, что за n дней цена опциона будет в интервале от w2 S до w3 S. Для статистических исследований использовать 20+n испытаний. Для моделирования использовать статистические пакеты, MS-Excel и др. приложения. Значения параметров задания для вариантов приводятся в таблицах 13 и 14, где S – первоначальная цена; p1 – вероятность увеличения цены опциона; u– коэффициент увеличения цены опциона; d– коэффициент уменьшения цены опциона. Таблица 13
Таблица 14
Рекомендуемая литература 1. Уотшем Т.Дж., Паррамоу К. Количественные методы в финансах: Учебное пособие для вузов. – М.: Финансы, ЮНИТИ, 1999. – 527 с. 2. Капитоненко В.В. Финансовая математика и ее приложения: Уч.-практ. пособие для вузов. – М.: ПРИОР, 1999. – 144 с. 3. Жак С.В. Математические методы в менеджменте и маркетинге. – Ростов н/Д: ЛаПО, 1997. – 320 с. 4. Динамическое программирование. Методические указания к лабораторной работе / Э.А.Мамаев, А.И. Филоненков, Т.В. Кречет. – Ростов н/Д: РГУПС, 1998. – 20 с. 5. Экономико-математические методы и прикладные модели / Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. – 391с. 6. Ковалев В.В., Уланов В.А. Курс финансовых вычислений. -М.: Финансы и статистика, 2001. – 328 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||