ММ Чуравский. Моделирование плазменного потока. Плазменная частота. Элементарные процессы в плазме. Дебаевский радиус Выполнил студент гр мМвтм11 Чуравский Д. С
 Скачать 129.73 Kb. Скачать 129.73 Kb.
|
Плазменная частотаИтак, в плазме возможно самопроизвольное разделение зарядов на расстоянии порядка 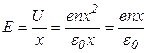 . .Второй закон Ньютона как уравнение движения: 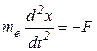 (знак «-» обусловлен тем, что сила, действующая на электрон, направлена в сторону, противоположную направлению смещения от положения равновесия, а электрон в процессе движения «проскакивает» положение равновесия – возникают колебания). Обозначим 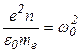 , ,тогда уравнение примет вид: 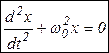 Это уравнение описывает колебательные движения с собственной круговой частотой 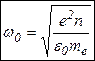 (Замечание. Величина
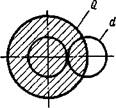
 Рисунок 1 – Падение радиоволны на ионосферу Показатель преломления ионосферы 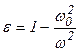 , т.е. , т.е. Элементарные процессы в плазме ЭФФЕКТИВНОЕ СЕЧЕНИЕ ВЗАИМОДЕЙСТВИЯ После возбуждения разряда ионизация в газе может происхо дить в основном двумя путями: взаимным соударением частиц и поглощением квантов энергии (фотоионизация). Одновременно идут процессы деионизации, т. е. образование нейтральных частиц при взаимодействии ионов и электронов. Длину свободного пробега частицы Л, среднее время пробега т = A/v и число столкновений частиц за 1 с v = 1/т можно свя зать с характеристиками, определяющими самый процесс столк новения частиц, введя понятие об эффективном сечении столк новения Q, которое для обычных газов часто называют газокине тическим. Для того чтобы произошло столкновение, центры молекул должны находиться на минимальном расстоянии, равном диамет ру d частицы. Принимая модель упругих шаров (рис. 2), легко видеть геометрический смысл сечения Q — это площадь круга радиусом, равным сумме радиусов сталкивающихся частиц. При учете движения обеих частиц принимают Q = V2 nd Длина пробега Л будет зависеть как от Q, так и от я — кон центрации частиц в 1 м3. Определяя относительную долю площа ди, занятой частицей, через слой газа единичной площади тол щиной dx (рис. 2.10), получим вероятность соударения на длине dx, равную nQ/1. С другой стороны, вероятность столкновения частиц при ма лом dx соответствует отношению толщины слоя dx к длине про бега Л и равна dx/X. Следовательно, dx/A. = nQdxj 1
Л= I/(nQ)
т = 1 /{vnQ). Оказывается, для молекул газокинетическое сечение Q мало зависит от их энергии (при высоких температурах). В то же вре мя чем больше размеры частиц, тем меньше их пробег. Кроме того, согласно уравнению Клапейрона А=1 /(nQ) = kT/{pQ).
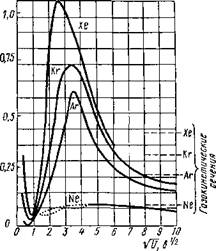
Подставляя значение 6= 1,38-10 23 Дж/К и р= 1,01X X Ю5 Па, получим Л = 1,36- 10_28(7/Q). Иногда эффективное сечение дается не для одной пары час тиц, а на 1 м3 газа. Тогда S = nQ. Наличие сил кулоновского взаимодействия между электро нами и ионами делает их соударения в плазме значительно более сложными, чем соударения нейтральных частиц. Вместо броунов ского зигзагообразного движения молекул траектория заряжен ной частицы становится извилистой, соответствующей измене ниям (флуктуациям) электрического поля в плазме. Поэтому в плазме, вообще говоря, должны учитываться все возможные сечения соударений: ион — атом— Q, a (перезарядка); ион — ион — Qu (сечение Гвоздовера); электрон — атом — Qea (сечение Рамзауэра); электрон — ион — Qei (прилипание или захват элек трона) и электрон — электрон Qee. Тогда для k видов частиц А. е = I /(EktikQek). Однако практически в сварочных дугах достаточно учитывать только Qea или Qe = Qea + Qei, так как другие сечения сравнительно малы. ЭФФЕКТ РАМЗАУЭРА Вероятность соударения Qea оценивается так называемым сечением Рамзауэра, которое в отличие от газокинетического сильно зависит от энергии электронов (рис. 3). При малых энергиях электронов в тяжелых благородных газах взаимодей ствие электронов с атомами сильно ослабляется в связи с эффектом Рамзауэра. Это объясняется волновым характером поведения электрона в процессе его упру гого взаимодействия. При определенном соотношении между длиной волны де Бройля А Б=й/(тв), соответствующей медленно движущемуся электрону, и размерами атома созда ются условия для сравительно беспрепятственного прохождения волны через атом, что дает малое сечение Qea. В условиях обычных сварочных дуг при 5000 К < Тст < < 12 000 К значения полных сечений Рамзауэра для взаимодей ствий Qe = Qea - f - Qeiy вычисленные Меккером, составляют от * (2...5) • 1016 см2 для инертных газов до 5-1014 м2 для щелочных металлов, т. е. отличаются почти в 200 раз. Возникает вопрос: когда и какие именно значения пробега или эффективного сечения следует применять в расчетах? Из рис. 2.11 видно, что эффект Рамзауэра и минимум сечения Se = nQe соответствуют энергиям электрона порядка ей « 1 эВ.
В плазме столба сварочной дуги при Т„ = 5000... 10 ООО К, как будет показано ниже, средняя энергия электронов, имеющих максвелловское распределение скоростей, равна 2kT и составляет как раз 1,0...2,0 эВ. Поэтому для плазмы в инертных газах сле дует брать Ае = 1/Se, что отвечает минимуму соответствующей данному газу кривой Рамзауэра. В переходных областях дуги температуры электронов Те и газа Тл отличны, термическое равновесие не соблюдается (Те ф Ф ТЛ) и электроны могут набирать энергию до (0,5... 1,0) и, или ив, т. е. до 10...20 эВ. На рис. 3 это примерно соответствуетгазокинетическим сечениям молекул. Средний газокинетический пробег иона в слабых полях Л, мало отличается от пробега молекул, т. е. для ионов (если диа метры иона и молекулы считать равными) В сильных полях, где и, > vH, молекулы можно считать непод вижными, тогда A,= V1>A7 Скорость электронов и в слабых полях много больше скорос ти молекул Ve vM. Кроме того, согласно кинетической теории газов электрон можно считать точкой (de <С du). Это значит, что электрон может подойти к центру молекулы на расстояние d/2, поэтому площадь круга эффективного соударения Qea будет вчет веро меньше. Учитывая это, получим газокинетический пробег электрона: Ле = л/2 -4ЛМ « 5,6ЛМ. Например, в воздухе при Т = 300 К и атмосферном давлении для газов = 1-10-7 м. В плазме при Т = 6000 К Лм будет в 20 раз больше [см. фор мулу (2.12)], а 20-5,6-ИГ7 = 10“5 м. Такое значение А[1] ( 10-5 м) часто принимают при расчете в переходных зонах дуги наряду с Л,« 107 м. Вычисленный по Рамзауэру пробег электрона в плазме Ае может отличаться от газокинетического в десятки раз. УПРУГИЕ И НЕУПРУГИЕ СОУДАРЕНИЯ Электрическое поле дуги напряженностью £ сообщает за 1 с энергию /£ электронам и ионам в 1 м3 столба. Электроны в связи с подвижностью воспринимают наибольшую часть этой энергии и в результате соударений передают ее атомам и ионам. Возможны два рода соударений — упругие и неупругие. Электрон, который близко подходит к атому, отталкивается электронным облаком, но нарушает, в свою очередь, располо жение облака. Окончательный результат зависит от скорости электрона (его энергии и направления движения). Медленный электрон легко отражается, а атомное электронное облако пре терпевает лишь незначительное возмущение; это так называемое упругое соударение. Классически его можно представить как столкновение двух идеально упругих шаров, обменивающихся кинетической энергией. Изменения потенциальной энергии атома здесь не происходит. Результатом упругих соударений электрона с тяжелыми частицами будет увеличение кинетической энергии последних, т. е. повышение температуры плазмы. Энергия тепловых электронов в сварочной дуге составляет порядка 1 эВ, так как ЮуПр = mv2/2 = (3/2)6Т, и если Т « 5800 К, a k яг 1/11 600 эВ/К, то кТ = 0,5 эВ, а (3/2) kT — 0,75 эВ. Обычно тепловую энергию оценивают значе нием kT, а не (3/2) kT. Запасаясь в возбужденных атомах, энергия вновь уходит из них в виде излучения — столб дуги светится. ПОТЕНЦИАЛ ИОНИЗАЦИИ Ионизацию можно рассматривать как крайний случай воз буждения, когда электрону сообщается энергия большая, чем самый высокий возбужденный уровень атома. Энергию, которая должна быть сообщена электрону для его ионизации, часто выражают в вольтах (точнее в электрон-воль тах) и называют соответственно потенциалом ионизации — U. Неупругие соударения частиц между собой при высоких тем пературе и плотности газа приводят к так называемой терми ческой ионизации, которая возникает за счет кинети ческой энергии частиц. После неупругого соударения оба электрона будут обладать малыми скоростями и вновь начнут ускоряться электрическим полем. Ионизация холодной плазмы осуществляется весьма неболь шим числом высокоскоростных электронов, соответствующих «хвосту» максвелловского распределения. Поэтому неупругих столкновений в сварочном столбе дуги обычно значительно мень ше, чем упругих. Энергия ионизации зависит от строения атома, т. е. от его места в периодической системе элементов. Она представляет собой периодическую функцию атомного номера элемента Z и снижается с уменьшением номера группы и уве личением номера периода таблицы Менделеева. Фотоионизация Атомы и молекулы могут возбуждаться не только при соударениях между собой или с ионами и электрона ми, но и путем поглощения квантов излучения. Такие кванты в дуге появляются при рекомбинации других сильно возбужден ных атомов. Условие фотоионизации: hv > eU„ где h = 4,13-10-15 эВ-c — постоянная Планка. Имея в виду, что частота колебаний v = с/А, где с — скорость света, можно определить длину волны Л, элек тромагнитного излучения, м, способного вызвать ионизацию ато мов: Л, = hc/(eUi) — 4,13-10—15 • 3 - 0ia/(eUl) = 12,4 • 10-7/(et/I). Чем больше потенциал ионизации элемента Ut, тем меньше требуемая Л,. Для сварочной дуги, где U, лежит в пределах 4... 25 эВ, соответствующие длины волн находятся в ультрафиолето вой части спектра. Фотоионизация в плотной плазме, видимо, незначительна по сравнению с термической ионизацией, причем выделить их доли расчетным и опытным путем пока не удается. Деионизация В любой точке стационарного разряда концент рация заряженных частиц любого типа определяется равенством скоростей образования и потерь частиц в этой точке. Иониза ция в плазме приводит к разделению зарядов, но электрическое притяжение ограничивает степень возможного разделения и плазма, как будет показано ниже, остается квазинейтральной. Наряду с ионизацией непрерывно происходят уравновешивающие ее процессы деионизации. К ним относятся рекомбинация заря женных частиц в нейтральные, захват электронов (прилипание), дрейф проводимости и диффузионные процессы, выравнивающие концентрацию (амбиполярная диффузия). Рекомбинация Скорость рекомбинации ионов, электронов н нейтральных частиц при их концентрации л,, пе, п определяется коэффициентом рекомбинации R по уравнению drh/dt = drie/dt = dn/dt — — Rn3, причем коэффициент R тем больше, чем больше плотность час тиц. Он зависит также от типа частиц, времени их жизни и раз меров ионов, от наличия близко расположенных тел (нейтраль ных атомов воздуха или охлаждающих стенок). Проводимость газового промежутка определяют прежде всего электроны как высокоподвижные частицы. Захват электронов атомами (прилипание) и ионами в процессе рекомбинации мож но в некоторых случаях рассматривать как процесс обратимый, а в других — как практически необратимый процесс. Например, процесс Na+ + e^Na° можно считать обрати мым. Если же при сварке в состав покрытия или флюса вводят плавиковый шпат СаИг, то в этом случае может происходить необратимый захват электрона фтором. Захват электронов с образованием тяжелых отрицательных ионов может осуществляться и другими атомами металлоидов, которые обладают довольно большим сродством к электрону (3...4 эВ). Дебаевский радиус Рассмотрим газообразную среду, состоящую из ионов и электронов. Распределение заряженных частиц в пространстве в достаточно большом объеме должно быть достаточно равномерным. В противном случае возникло бы электрическое поле, стремящееся сблизить разноименные заряды и сгладить неравномерность распределения.
Рассмотрим распределение плотности заряда в окрестности произвольно выбранной заряженной частицы. Такая частица будет отталкивать одноименные заряды и притягивать заряды разноименного знака (рис. 4). 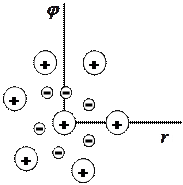 Рисунок 4 – Пример частицы. Найдем зависимость потенциала результирующего поля, созданного выбранной (пробной) частицей и ее окружением. Запишем теорему Гаусса в дифференциальной форме 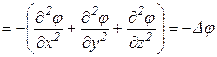 (**), где (**), где Сравнивая (*) с (**) получаем уравнение Пуассона При максвелловском распределении по скоростям связь потенциала и концентрации ионов определяется формулой Больцмана где Для электронов с учетом знака соответственно (плазму считаем равновесной): где Подставляем последние выражения в уравнение Пуассона: В случае низкотемпературной плазмы 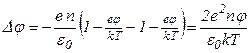 . .Решение этого уравнения: 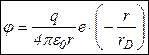 где 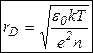 - радиус Дебая. - радиус Дебая.Физический смысл радиуса Дебая: на расстоянии, равном (Замечания. 1. Характерная длина Рассмотрим другой, упрощенный подход к решению задачи о масштабе нарушения квазинейтральности. Выделим в плазме плоский слой площадью
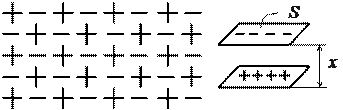 Плоский слой можно рассматривать как конденсатор, напряжение на котором 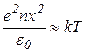 . .Получаем характерный размер области, в которой возможно отклонение от нейтральности, – дебаевскую длину 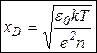 К такой же характерной длине мы пришли, рассматривая вопрос об экранировании электрического поля в плазме ( Роль длины Дебая как радиуса экранирования и как пространственного масштаба разделения зарядов выражена определением плазмы Ленгмюра: совокупность свободно движущихся разноименно заряженных частиц, т.е. ионизированный газ, называется плазмой, если длина Дебая мала по сравнению с линейным размером объема, занимаемого газом. Пока радиус Дебая мал по сравнению с размером Заключение Моделирование плазменного потока трудоемкий процесс, который изрядно зависит от ряда формул и определенных параметров. Все параметры следует учитывать, ведь исходя из всего вышеизложенного, следует отметить, что даже малейшая закономерность играет весомую роль в каждом процессе или отвечает за определенную функцию. Список литературы.
дат, 1963. Т. 1. С. 183–272.
|