курс. хищник-жертва. Моделирование в научных исследованиях стало использоваться еще в глубокой древности и постепенно захватывало все новые области научных знаний
 Скачать 224.39 Kb. Скачать 224.39 Kb.
|
Классификация моделейКлассификация – это разделение объектов на группы, имеющие один или несколько общих признаков. В зависимости от признака классификации одни и те же модели могут быть отнесены к разным классам. Классификация по области использования модели представлена на рис. 1.2. 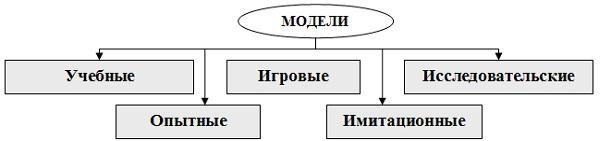 Рис. 1.2. Классификация моделей по области использования Учебныемодели– наглядные пособия, тренажеры, обучающие программы. Игровыемодели– это экономические, военные, деловые игры. Они репетируют поведение объекта в различных ситуациях. Исследовательскиемоделисоздаются для исследования процессов или явлений, например, стенды для проверки электронной аппаратуры. Опытные модели – это уменьшенные или увеличенные копии объектов. Их используют для исследования объекта и прогнозирования его будущих характеристик (например, опытная модель проектируемого автомобиля). Имитационныемоделиимитируют реальность, при этом, как правило, эксперимент многократно повторяется. Классификация по отрасли представленных в модели знаний разделяет все модели на физические, биологические, социальные, экономическиеи т. д. Классификация по способу представления моделиОтразить в модели признаки оригинала можно разными способами. Можно скопировать признаки, построив натурную (материальную) модель. Примерами натурных моделей являются макеты и муляжи – уменьшенные или увеличенные копии, воспроизводящие либо внешний вид объекта (например, глобус), либо его структуру (например, модель Солнечной системы), либо поведение (например, радиоуправляемая модель автомобиля). Можно построить модель объекта, описав его свойства на одном из языков кодирования информации – дать словесное описание, привести формулу, чертеж, рисунок. Такая модель называется информационной моделью. Замена реального объекта его формальным описанием, т. е. его информационной моделью, называется формализацией.Существуют разные формы представления информационных моделей: словесные (вербальные), графические, математические, табличные и др. (рис. 1.3). Вербальнаямодель– информационная модель в мысленной или разговорной форме. Знаковаямодель– информационная модель, выраженная знаками, т. е. средствами любого формального языка. Математическаямодель– модель, представленная с помощью математических формул. Логическаямодель– это модель, в которой представлены различные варианты выбора действий на основе умозаключений и анализа условий. Специальныемодели– это, например, химические формулы, ноты и т. д. 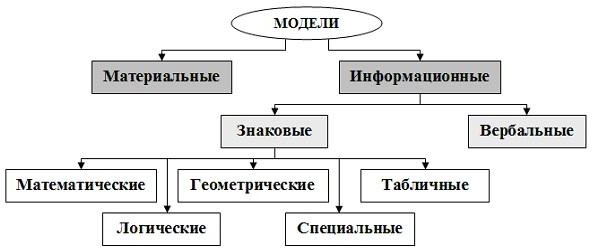 Рис. 1.3. Классификация моделей по способу представления Геометрическая модель – модель, представленная с помощью графических форм (граф, блок-схема алгоритма решения задачи, диаграмма). Граф – это множество вершин и множество ребер, соединяющих между собой все или часть этих вершин. На рис. 1.5,а показана геометрическая модель в виде графа, представляющая схему дорог, соединяющих населенные пункты. Вершины графа – это населенные пункты, ребра – дороги. Построенная модель позволяет, например, ответить на вопрос: через какие населенные пункты нужно проехать, чтобы добраться из пункта А в пункт В. Однако, эта модель не позволяет ответить на вопрос, сколько составит расстояние от одного населенного пункта до другого. На этот вопрос можно ответить с помощью модели в виде взвешенногографа, каждое ребро которого отмечено числом, равным по значению расстоянию между соответствующими населенными пунктами (рис. 1.4,б).  Рис. 1.4. Модель в виде графа Табличнаямодель– это информация о моделируемом объекте, структурированная в виде таблицы. Различают следующие типы табличных моделей: таблица типа «объект-свойство» в одной строке содержит информацию об одном объекте в виде заданного набора его свойств таблица типа «объект-объект» отражает взаимосвязи между разными объектами по какому-либо свойству таблица типа «двоичная матрица» является частным случаем таблицы «объект-объект» и отражает наличие или отсутствие связи между объектами Классификация по характеру отображаемых свойств объекта моделированияПо характеру отображаемых свойств выделяют два типа моделей: структурные– отражают структуру (устройство) моделируемого объекта, существенные для целей исследования свойства и взаимосвязи компонентов этого объекта; функциональные– отражают внешне воспринимаемое поведение (функционирование) объекта. Функциональные модели часто строятся как модели черного ящика рис. 1.5. Название «черный ящик» образно подчеркивает отсутствие сведений о внутреннем содержании объекта. 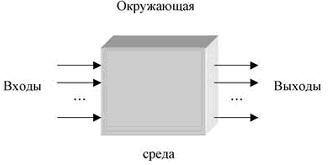 Рис. 1.5. Модель «черного ящика» Наряду с моделью черного ящика по степени информированности исследователя о моделируемом объекте, выделяют еще два вида моделей: «белыйящик»– известно все о внутреннем содержании объекта; «серыйящик»– известна структура объекта, неизвестны количественные значения параметров. Классификация с учетом фактора времениС учетом фактора времени модели можно разделить на два класса: статическиемодели– это одномоментный срез информации по объекту; динамическиемоделипозволяют увидеть изменение объекта во времени. Например, медицинская карта состояния здоровья пациента в поликлинике отражает изменение состояния здоровья человека за некоторый период времени (динамическая модель), а медицинское обследование при поступлении на работу дает картину состояния здоровья на данный момент времени (статическая модель). Классификация по характеру изменения модели во времени охватывает динамические модели и выделяет два типа моделей: непрерывные–изменяют свое состояние во времени за сколь угодно малое приращение времени; дискретные – изменяют свое состояние во времени дискретно, через определенный временной интервал. Классификация по признаку причинной обусловленности выполняется в зависимости от возможности или невозможности учета в рассматриваемой модели одного или нескольких случайных факторов, при этом выделяют два вида моделей: детерминированные – модели, в которых все воздействия и факторы определены и известны заранее; стохастические(вероятностные)– модели, в которых хотя бы один из факторов носит случайный характер. По способу реализации информационные модели делятся на компьютерные и некомпьютерные. Компьютерная модель – модель, реализованная с помощью программных средств на компьютере. Программное обеспечение, средствами которого может осуществляться компьютерное моделирование, может быть как универсальным (например, текстовые или табличные процессоры), так и специализированным, предназначенным лишь для определенного вида моделирования. 1.5. Опыт лучших учителей при преподавании моделирования Аникова Юлия Александровна, кандидат педагогических наук, педагог дополнительного образования МБУ ДО ЦДТТ «Юный автомобилист». В сентябре 2018 года в Центре детского технического творчества «Юный автомобилист» под ее руководством впервые было создано творческое объединение «3D-моделирование». Это направление интересно, перспективно, востребовано. В настоящее время в мире, да и в России, сложно найти ту отрасль экономики, где бы не использовались 3D технологии: промышленность, концептуальное моделирование, проектирование и разработки - 42%, архитектура и строительство - 18%, товары народного потребления – 14% , медицина и здравоохранение – 6% и т.д. И с каждым годом масштабность внедрения 3D-моделирование в разные отрасли экономики только увеличивается. Возникает целый ряд нерешённых педагогических вопросов: Как организовать обучение 3D-моделированию в учреждении дополнительного образования? С какого возраста принимать детей в творческое объединение? Какое компьютерное программное обеспечение использовать для работы? К настоящему времени накоплен определенный опыт преподавания 3D-моделирования на факультативах в школах и в дополнительном образовании. Интересен опыт обучения младших школьников 3D – моделированию в программной среде Autodesk Tinkercad педагогами из Кемеровского государственного университета (Можаровыми) Санкт-Петербургская педагогическая школа, в частности, Огановская Е.Ю., Гайсина С.В., Князева И.В. предлагают интегративный курс «Робототехника, 3D-моделирование и прототипирование в дополнительном образовании» (12 лет – Creo, 13 лет - Blender, 14 лет - Компас -3D). Она обобщила педагогический опыт и разработала дополнительную образовательную общеразвивающую программу «3D-моделирование». Цели: Развитие у учащихся творческих способностей, пространственного воображения и объемного видения. Формирование геометро-графической системы знаний и практических умений. Освоение методов и алгоритмов создания трёхмерных моделей реальных и абстрактных объектов в современных системах 3D-моделирования. Программа «3D-моделирование» рассчитана на один год, возраст учащихся – с 9лет. Программа рассчитана на 144 часа при 2-х часовом занятии два раза в неделю. Программа содержит 5 разделов: 1 раздел «Приёмы графического оформления чертежей». Актуальность этого раздела очевидна, так как в настоящее время во многих школах России упразднили такой учебный предмет, как «Черчение». Я считаю, что это огромное упущение. Многие ребята на входном тестировании в творческое объединение показали слабые геометро-графические знания и умения. Многие вопросы и задания поставили детей в тупик. Поэтому было принято решение начать с черчения в тетради и на формате А4. Изучали Государственные стандарты на составление и оформление чертежей ГОСТ 2.301-2.304, 2.307. Знакомились с понятия: единая система конструкторской документации, форматы, линии чертежа, масштаб, чертёжный шрифт, нанесение размеров. Правила оформления форматов, основная надпись. Аксонометрическая проекция, развёртка. 2 раздел «SketchUp - программа трёхмерной визуализации». На изучение этого раздела отводится 16 часов. За это время ребята изучают программу и выполняют 6 практических отдельных заданий: Проектирование частного загородного дома. Проектирование коттеджного посёлка. Моделирование элементов интерьера. Создание стола, стула, табурета, дивана, кровати. Моделирование тел вращения. Создание вазы, торшера, люстры. Проектирование авторского брелка с 3D-надписью. Индивидуальное задание «Мой мир» (например, проектирование комнаты моей мечты, завода будущего, капсульной башни, таможенного пункта и т.д.) Реализация 3и 4 раздела программы стала возможна благодаря тому, что Центр детского технического творчества «Юный автомобилист» несколько лет назад вошел в программу «3D-образование» и имеет бесплатный доступ ко всеем лицензионным, обновлённым продуктам компании Autodesk. Юлия Александровна, руководитель творческого объединения, ещё в 2007 году прошла обучение по основным продуктам компании Autodesk в аккредитованном центре с правом преподавания этих программ в любой стране мира. 3 раздел «Autodesk AutoCAD» -программа 2D и 3D проектирования. Ребята изучают систему автоматизированного проектирования AutoCAD на протяжении 34 часов, совершенствуют геометро-графическую подготовку, создавая технические электронные 2D-чертежи. 4 раздел посвящается одной из самых востребованных в мире систем автоматизированного проектирования «Autodesk Inventor». На изучении этого раздела отводится 40 часов. Вот перечень некоторых практических работ: Создание 3D-тел вращения: сфера, тор, цилиндр, конус. Моделирование напольной вазы, шкатулки, архитектурной колонны. Моделирование деталей с переменным сечением. Проектирование гребного винта. Проектирование болтового соединения. Создание рабочего чертежа. Заключительным разделом программы является «Творческий проект» - отводится 24 часа. Примером такого творческого проекта является «Велопарковка». Этот проект принимал участие в областном конкурсе технического творчества «Модель своими руками» в номинации «Благоустройство городской среды». В финале конкурса автор проекта получил диплом 3 степени. Итог: изучены 3 востребованные компьютерные программы – значит, было интенсивно; 38 ученических проекта на стадии завершения – значит, было продуктивно, из 5 учебных групп никто из ребят не ушёл – значит, было интересно. 2.1. Построение моделей на примерах моделирования отношений «Хищник-жертва» в природном сообществе Для исследования окружающей нас среды используют экологическое моделирование. Математические модели используют в тех случаях, когда нет естественной среды и нет естественных объектов, она помогает сделать прогноз влияния разных факторов на исследуемый объект. Данный метод берет на себя функции проверки, построения и интерпретацию полученных результатов. На основе таких форм экологическое моделирование занимается оценкой изменений, окружающей нас среды. В настоящий момент подобные формы используется для изучения окружающей нас среды, а когда требуется изучить какую-либо из ее областей, то применяют математическое моделирование. Данная модель дает возможность спрогнозировать влияние тех или иных факторов на объект изучения. В свое время был предложен тип «хищник – жертва» такими учеными как: Т. Мальтусом (Malthus 1798, Мальтус 1905), Ферхюльстом (Verhulst 1838), Пирлом (Pearl 1927, 1930), а также А. Лотки (Lotka 1925, 1927) и В. Вольтерры (Volterra 1926).Эти модели воспроизводят периодический колебательный режим, возникающий в результате межвидовых взаимодействий в природе. Одним из основных методов познания является моделировка. Помимо того, что в нем можно спрогнозировать изменения, происходящие в окружающей среде, к тому же помогает найти оптимальный способ решения проблемы. Уже давно в экологии используют математические модели, для того чтобы установить закономерности, тенденции развития популяций, помогают выделить суть наблюдений. Макет может служить образцом поведения, объекта. При воссоздании объектов в математической биологии используются прогнозирования различных систем, предусматриваются специальные индивидуальности биосистем: внутренне строение особи, условия жизнеобеспечения, постоянство экологических систем, благодаря которым сберегается жизнедеятельность систем. Появление компьютерного моделирования значительно раздвинуло рубеж способностей исследования. Возникло вероятность многосторонней реализации трудных форм, не допускающих аналитического изучения, появились новейшие направления, а еще имитационное моделирование. Рассмотрим, что же такое объект моделирования. «Объектом является замкнутая среда обитания, где происходит взаимодействие двух биологических популяций: хищников и жертв. Процесс роста, вымирания и размножения происходит непосредственно на поверхности среды обитания. Питание жертв происходит за счет тех ресурсов, которые присутствуют в данной среде, а питание хищников происходит за счет жертв. При этом питательные ресурсы могут быть как возобновляемые, так и не возобновляемые. В 1931 году Вито Вольтеррой были выведены следующие законы отношения хищник-жертва. Закон периодического цикла – процесс уничтожения жертвы хищником нередко приводит к периодическим колебаниям численности популяций обоих видов, зависящим только от скорости роста плотоядных и растительноядных, и от исходного соотношения их численности. Закон сохранения средних величин – средняя численность каждого вида постоянна, независимо от начального уровня, при условии, что специфические скорости увеличения численности популяций, а также эффективность хищничества постоянны. Закон нарушения средних величин – при сокращении обоих видов пропорционально их числу, средняя численность популяции жертвы растет, а хищников – падает. Модель хищник-жертва – это особая взаимосвязь хищника с жертвой, в результате которой выигрывают оба. Выживают наиболее здоровые и приспособленные особи к условиям среды обитания, т.е. все это происходит благодаря естественному отбору. В той среде где нет возможности для размножения, хищник рано или поздно уничтожит популяцию жертвы, в последствии чего вымрет и сам». На земле существует множество живых организмов, которые при благоприятных условиях увеличивают численность сородичей до огромных масштабов. Такая способность называется: биотический потенциал вида, т.е. увеличение численности вида за определенный промежуток времени. Каждый вид имеет свой биотический потенциал, к примеру крупные виды организмов за год могут возрасти всего в 1,1 раза, в свою очередь организмы более мелких видов, таких как рачки и т.д. могут увеличить свой вид до 1030 раз, ну а бактерии еще в большем количестве. В любом из этих случаев популяция будет расти в геометрической прогрессии. Экспоненциальным ростом численности называется геометрическая прогрессия роста численности популяции. Такую способность можно наблюдать в лаборатории у бактерий, дрожжей. В не лабораторных условиях экспоненциальный рост возможно увидеть на примере саранчи или же на примере других видов насекомых. Такой рост численности вида можно наблюдать в тех местах где у него практически нет врагов, а продуктов питания более чем достаточно. В конце концов увеличение вида, после того как численность возросла в течении непродолжительного времени, рост популяции начинал снижаться. Рассмотрим компьютерную модель размножения млекопитающих на примере модели Лотки-Вольтерры. Пусть на некоторой территории обитают два вида животных: зайцы и волки. Математическая модель изменения численности популяций в модели Лотки-Вольтерры. 2.2. Решение задачи математического моделирования хищник-жертва в Excel Цель – составить упрощенную математическую модель взаимоотношений хищника и жертвы в природном сообществе. Начальная численность популяции зайца (жертвы) – 1000 особей. Nз0 = 1000. Начальная численность популяции волка (хищник) – 20 особей. Nв0 = 20. Выжившая к концу каждого года часть популяции зайца увеличивает свою численность на 30 %. Рз = 0,3. Годовой прирост популяции волков – 10%. Рв = 0,1. Один волк потребляет по 40 зайцев ежегодно. R1в = 40. Смертность зайца по иным причинам равна нулю. Смертность волков равна нулю. Задача №1. Условие. Рассчитать, какова будет численность популяции зайца через 1,3,5 и 10 лет при полном отсутствии волков. Отобразить изменения численности зайцев в течение данного периода графически. Решение. Nз0 = 1000 Nз = Nз0 + Nз0 * Рз Рз = 0,3; Nз = ? Используем ячейки В5 – В15. Формула для вычислений : В6 = $A$1 =B5+B5*$B$1. Ячейки В7 – В15 заполняем вниз по образцу. Задача №2. Условие. Рассчитать, какова будет численность популяции зайца через 1, 3,5 и 10 лет, если начальная численность волков составляет 20 особей и не изменяется на протяжении указанного времени. Отобразить изменения численности зайцев в течение данного периода графически. Сравнить результат с результатами задачи №1. Решение. Nз0 = 1000 Nз = (Nз0 - Nв0* R1в) + (Nз0 - Nв0* R1в)* Рз Рз = 0,3 Nз = (Nз0 - Nв0* R1в) * (1+ Рз) Nв0 = 20. R1в = 40. Рв = 0. Nз = ? Для популяции волков используем ячейки F 5 – F 15. Присваиваем F5 = $C$1. Дальше копируем вниз по образцу (популяция волка не меняется по условию). Для популяции зайцев используем ячейки С5 – С15. Присваиваем С5 = $C$1. Формула: С6 = (C5-F5*$D$1)*(1+$B$1). Ячейки С7 – С15 заполняем вниз по образцу. Задача №3. Условие. Рассчитать, какова будет численность популяции зайца через 1, 3,5 и 10 лет, если начальная численность волков составляет 20 особей и возрастает на 10% ежегодно Отобразить изменения численности зайцев в течение данного периода графически. Сравнить результат с результатами задачи №1и №2. Решение. Nз0 = 1000 Nз = (Nз0 - Nв* R1в) + (Nз0 - Nв0* R1в)* Рз Рз = 0,3 Nз = (Nз0 - Nв* R1в) * (1+ Рз) Nв0 = 20. Nв = Nв0 + Nв0* Рв R1в = 40. Рв = 0,1. Nз = ? Для популяции волков используем ячейки G5 – G15. Присваиваем G5 = $C$1. G6 =G5+G5*$E$1. Для популяции зайцев используем ячейки D5 – D15. Присваиваем D5 = $A$1. Формула: D6 =(D5-G5*$D$1)*(1+$B$1). Ячейки D7 – D15 заполняем вниз по образцу. Задача №4. Условие. Рассчитать, какой должна быть начальная численность растущей популяции волков, чтобы численность зайцев была относительно стабильной (то есть равнялась приблизительно 1000) в течение первых пяти лет существования популяции. Как будет изменяться численность популяции зайца в течение следующих пяти лет? Представьте данные графически. Решение. Nз0 = 1000 Nз = Nз0 Рз = 0,3 Nз = (Nз - Nв* R1в) * (1+ Рз) R1в = 40. Nв = Nв0 + Nв0* Рв Рв = 0,1. Nв0 = ? Для популяции волков ячейки H5 – H15. В задаче требуется подобрать такое начальное количество волков, при котором численность зайцев будет минимально изменяться в течение первых пяти лет существования. Подбирать начальное число будем в ячейке Н1. Поэтому ячейке Н5 присваиваем значение $H$1. H5 = $H$1. H6 =H5+H5*$E$1. Для популяции зайцев используем ячейки E5 – E15. E5 = $A$1. Формула: E6 =(E5-H5*$D$1)*(1+$B$1). Ячейки E7 – E15 заполняем вниз по образцу. Изменяя число в ячейке Н1, подбираем значения в ячейках Е5 – Е9 примерно равные 1000. Такими значениями будут 5 и 6. Наиболее удачное значение – 6 (начальная популяция волков). Составление электронной таблицы В первую строку таблицы вносим константы, входящие в условие : A1 – начальная численность зайцев, Nз0 = 1000. B1 – ежегодное увеличение популяции зайцев, Рз = 0,3 . C1 – начальная численность волков, Nв0 = 20. D1 – количество зайцев, поедаемых одним волком за год, R1в = 40. E1 – годовой прирост численности волков, Рв = 0,1. Решение запишем в ячейки, расположенные ниже. В экологии начальным годом принято считать «нулевой» год, поэтому годы пронумеруем от 0 до 10. В ячейки B5 – F5 присваиваем $A$1 – начальная численность зайцев, Nз0. В ячейки F5, G5 присваиваем $C$1 – начальная численность волков, Nв0 . (В первом задании волки не упоминаются, ячейка H5 заполняется отдельно по условию задачи № 4) .
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
