Практическая работа. Модель Хищник-Жертва. Моделирование

• Название: Моделирование
• Дата: 14.10.2021
• Размер: 357.5 Kb.
• Имя файла: Практическая работа. Модель Хищник-Жертва.doc
• Тип: Документы; #247792

И
20.10.2021
нформатика, 11 класс К.Ю. Поляков, Е.А. Еремин

2. Моделирование

Практические работы

6. 
   Моделирование работы процессора

Уровень А.

1. 
   Напишите программу, которая моделирует работу процессора. Процессор имеет 4 регистра, они обозначаются R0, R1, R2 и R3. Все команды состоят из трех десятичных цифр: код операции, номер первого регистра и номер второго регистра (или число от 0 до 9). Коды команд и примеры их использования приведены в таблице:
   

Код операции	Описание	Пример	Псевдокод
1	запись константы	128	R2 := 8
2	копирование значения	203	R3 := R0
3	сложение	331	R1 := R1 + R3
4	вычитание	431	R1 := R1 – R3

Обратите внимание, что результат записывается во второй регистр. Команды вводятся последовательно как символьные строки. После ввода каждой строки программа показывает значения всех регистров.

Уровень B.

2. 
   Добавьте в систему команд умножение, деление и логические операции c регистрами – «И», «ИЛИ», «исключающее ИЛИ».
   
3. 
   Добавьте в систему команд логическую операцию «НЕ». Подумайте, как можно использовать второй регистр.
   

Уровень С.

4. 
   Сделайте так, чтобы в команде с кодом 1 можно было использовать шестнадцатеричные значения констант (0-9, A-F).
   

Уровень D+.

5. 
   Добавьте обработку ошибок типа «неверная команда», «неверный номер регистра», «деление на ноль».
   
6. 
   *Добавьте команду «СТОП», которая прекращает работу программы. Введите строковый массив, моделирующий память, и запишите в него программу – последовательность команд. Ваша программа должна последовательно выполнять эти команды, выбирая их из «памяти», пока не встретится команда «СТОП».
   
7. 
   **Подумайте, как можно было бы организовать условный переход: перейти на N байт вперед (или назад), если результат последней операции – ноль.
   

6. 
   Искусственный интеллект

Уровень А.

1. 
   Откройте браузер на странице quickdraw.withgoogle.com. Попробуйте выполнить задание – нарисовать несколько предметов, которые нейронная сеть попробует угадать. Сколько из нарисованных вами изображений нейронная сеть определила правильно?
   

Ответ:

2. 
   С помощью сервиса color.artlebedev.ru раскрасьте чёрно-белое изображение (можно использовать файл boat.jpg или своё изображение) и добавьте в отчёт оригинал и полученное цветное изображение.
   

   Оригинал	Цветной вариант

3. 
   С помощью сервиса www.captionbot.ai, использующего нейронные сети, постройте подпись к вашему изображению и переведите её на русский язык.
   

Оригинал	На русском языке

Уровень B.

4. 
   С помощью сервиса www.how-old.net попытайтесь определить возраст человека, который изображен на фотографии (можно использовать свою фотографию или изображение girl.jpg).
   
5. 
   С помощью сервиса hi.cs.waseda.ac.jp:8082 выполните раскраску чёрно-белого изображения.
   

Оригинал	Цветной вариант

Сравните результат с тем, который был получении в п. 2.

6. 
   С помощью сервиса bigjpg.com/ru выполните увеличение какого-нибудь изображения в 4 раза (можно использовать файл flowers.png). Добавьте в отчёт оригинал и полученное увеличенное изображение.
   

Оригинал	Увеличенное изображение

Уровень С.

7. 
   Установите практикум по искусственному интеллекту с сайта www.lbai.ru (это нужно сделать заранее).
   
8. 
   Выполните лабораторные работы 1-4
   
9. 
   Зарегистрируйтесь на сайте letsenhance.io/ru/. С помощью этого сервиса попробуйте улучшить фотографию и увеличить её в 4 раза.
   

Оригинал	Увеличенное изображение

6. 
   Математическое моделирование

При выполнении этой работы можно использовать шаблон – электронную таблицу в файле Кредит.xls.

Уровень A.

1. 
   Дядя Ваня решил взять кредит 100 тыс. рублей в банке на год под 13% годовых. Банк предложил ему выплачивать каждый месяц равные суммы (такой платёж называется аннуитетным). Сумма ежемесячной выплаты p вычисляется по формуле:
   

,

где S – сумма кредита, i – годовая процентная ставка кредита, делённая на 12; n – число месяцев, в течение которых нужно выплатить кредит.

Используя электронную таблицу или программу на языке программирования, определите, сколько всего денег выплатит дядя Ваня банку по процентам (сверх 100 тыс. рублей).

Ответ:

Уровень B.

2. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня выплатит по процентам не более 10000 руб.
   

Ответ:

Какова в этом случае будет величина ежемесячной выплаты:

3. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня будет ежемесячно выплачивать не более 9100 руб.
   

Ответ:

Какова в этом случае будет общая сумма выплат:

Уровень С.

4. 
   Существует ещё один вариант выплаты кредита, при котором выплачиваемая сумма изменяется (уменьшается) каждый месяц. Такая схема называется дифференцированными платежами. Выплаты за текущий месяц складываются из двух частей – выплат p₁ за основную часть кредита (100 тыс. руб) и выплат по процентам p₂.
   

Первая часть, p₁, всегда постоянна и определяется как сумму кредита, делённая на количество месяцев. Для примеры, который рассмотрен в начале описания этой работы,

p₁ = 100000 : 12 = 8333,33 р.

Вторая часть, p₂, зависит от номера месяца k, поэтому будем обозначать её как p_2k. Она вычисляется как оставшаяся сумма основного долга, умноженная на годовую процентную ставку кредита, делённую на 12:



Например, в первый месяц выплат (выплат ещё не было), поэтому

p₂₁ = 100000  0,13 / 12 = 1083,33 р.

Во второй месяц оставшаяся сумма долга равна

S₁ = 100000 – 8333,33 = 91666,67 р.

При этом получается другая выплата по процентам:

p₂₂ = 91666,67  0,13 / 12 = 993,06 р.

5. 
   При ставке 13% постройте график выплат дяди Вани при дифференцированных платежах. Сколько всего денег он переплатит по процентам?
   

Ответ:

Какой способ выплат выгоднее для дяди Вани:

6. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня выплатит по процентам не более 10000 руб.
   

Ответ:

Какова в этом случае будет величина выплаты в первый месяц:

7. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня будет ежемесячно выплачивать не более 9100 руб.
   

Ответ:

Какова в этом случае будет общая сумма выплат:

6. 
   Моделирование движения

При выполнении этой работы можно использовать шаблон – электронную таблицу в файле Парашютист.xls.

Уровень A.

Парашютист массой 90 кг разгоняется в свободном падении до скорости 10 м/с и на высоте 50 м раскрывает парашют, площадь которого 55 м². Коэффициент сопротивления парашюта C = 0,9.

1. 
   Постройте графики изменения скорости и высоты полета в течение первых 4 секунд;
   

Ответ:

2. 
   Определите, через какое время и с какой скоростью приземлится парашютист?
   

Время:

Скорость:

3. 
   Сравните результаты моделирования с установившимся значением скорости, вычисленным теоретически.
   

	теоретически	моделирование
Скорость приземления, м/с	5,40	5,40

Уровень B.

4. 
   Напишите программу, которая моделирует полет мяча, брошенного вертикально вверх, при
   

мм, г, м/с, с.

Остальные необходимые данные есть в тексте § 10. Выполните следующие задания:

• 
  определите время полета, максимальную высоту подъема мяча и скорость в момент приземления;
  
• 
  вычислите время полета и максимальную высоту подъема мяча, используя модель движения без сопротивления воздуха:
  

• 
  сравните эти результаты с полученными при моделировании с учетом сопротивления;
  

  	без учёта сопротивления	с учётом сопротивления	ошибка (%)
  Время полета, с
  Максимальная высота, м
  Скорость приземления, м/с

• 
  можно ли в этой задаче пренебречь сопротивлением воздуха? почему?
  

Ответ:

• 
  с помощью табличного процессора постройте траекторию движения мяча, а также графики изменения скорости, ускорения и силы сопротивления (указание: из программы сохраните данные в CSV-файл, разделив данные в каждой строке точками с запятой);
  

Скорость:

Ускорение:

Сила сопротивления:

• 
  уменьшите шаг сначала до 0,01 с и повторите моделирование; затем выполните моделирование при шаге 0,001; сделайте выводы по поводу выбора шага в данной задаче.
  

Ответ:

Уровень C.

5. 
   *Выполните моделирование движения мяча, брошенного под углом 45° к горизонту (при тех же остальных условиях, что и в задаче уровня B):
   

• 
  определите время полета, максимальную высоту и дальность полета мяча, скорость в момент приземления;
  
• 
  сравните результаты со случаем, когда сопротивление воздуха не учитывается
  

  	без учёта сопротивления	с учётом сопротивления	ошибка (%)
  Время полета, с
  Максимальная высота, м
  Дальность полета, м
  Скорость приземления, м/с

• 
  сделайте выводы.
  

Ответ:

6. 
   Моделирование развития популяции

Для выполнения работы откройте файл-заготовку Популяция.xls.

Уровень A.

1. 
   Постройте графики изменения численности популяции животных для моделей ограниченного и неограниченного роста при , и в течение первых 15 периодов. Определите, когда модель неограниченного роста перестает быть адекватной (отклонение от модели ограниченного роста составляет более 10%).
   

Ответ:

2. 
   Используя подбор параметра, определите, при каких коэффициентах модель неограниченного роста остается адекватной в течение не менее 10 периодов.
   

Ответ:

3. 
   Используя модель ограниченного роста из предыдущей задачи, выполните моделирование популяции с учетом отлова ( ). Предполагается, что животных начали отлавливать через 10 лет после начала наблюдений.
   

• 
  постройте график изменения численности животных в течение 40 периодов;
  

• 
  Определите количество животных в состоянии равновесия по результатам моделирования;
  

Ответ:

• 
  Проверьте, зависит ли это значение от начальной численности?
  

Ответ:

Уровень B.

4. 
   Определите количество животных в состоянии равновесия теоретически, из модели ограниченного роста с отловом; сравните это значение с результатами моделирования
   

Ответ:

5. 
   Определите, на что влияет начальная численность животных;
   

Ответ:

6. 
   Определите (по результатам моделирования) максимальный отлов , при котором популяция не вымирает.
   

Ответ:

Уровень С.

7. 
   *Определите максимально допустимый отлов теоретически, из модели ограниченного роста с отловом; сравните это значение с результатами моделирования
   

Ответ:

Из какого условия вы нашли это значение?

6. 
   Моделирование эпидемии

Для выполнения работы откройте файл-заготовку Эпидемия.xls.

При эпидемии гриппа число больных изменяется по формуле

,

где – количество заболевших в -й день, а – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:

,

где – общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):

.

Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.

Выполните моделирование развития эпидемии при и до того момента, когда количество больных станет равно нулю.

Уровень A.

1. 
   Постройте график изменения количества больных.
   

Ответ:

2. 
   Когда закончится эпидемия?
   

Ответ:

3. 
   Сколько человек переболеет, а сколько вообще не заболеет гриппом?
   

Ответ:

4. 
   Каково максимальное число больных в один день?
   

Ответ:

Уровень B.

5. 
   Изменяя коэффициент с шагом 0,1, определите, при каких значениях модель явно перестает быть адекватной.
   

Ответ:

Уровень C.

6. 
   *Сравните модель, использованную в этой работе, со следующей моделью:
   

, .

Постройте график изменений количества больных этой и предыдущей моделей на одном поле:

Анализируя результаты моделирования, докажите, что эта модель неадекватна.

Ответ:

Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?

Ответ:

Сравните поведение двух моделей при , и . Сделайте выводы.

Ответ:

6. 
   Модель «хищник-жертва»

Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.

Выполните моделирование биологической системы «щуки-караси»



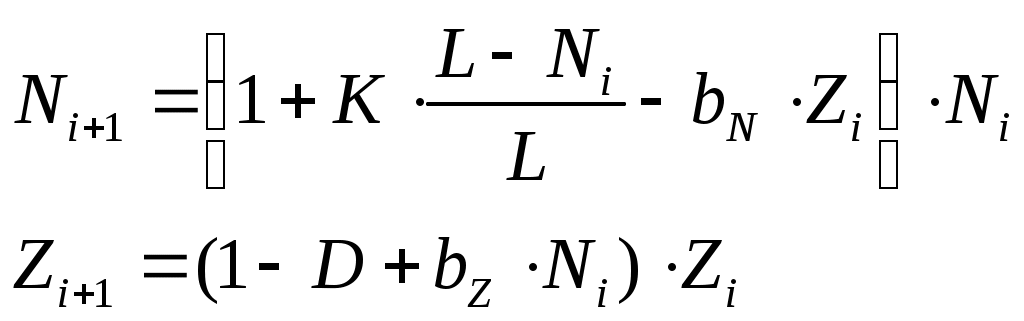
где – численность карасей

– численность щук

при следующих значениях параметров:

– коэффициент прироста карасей;

– предельная численность карасей;

– начальная численность карасей;

– начальная численность щук;

– коэффициент смертности щук без пищи;

и – коэффициенты модели.

Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.

Уровень A.

1. 
   Выполните моделирование двух популяций в течение 25 периодов. Постройте графики изменения численности карасей и щук.
   

Ответ:

2. 
   Сколько карасей и щук живут в водоеме в состоянии равновесия?
   

Ответ:

3. 
   Что влияет на количество рыб в состоянии равновесия: начальная численность хищников и жертв или значения коэффициентов модели?
   

Ответ:

Уровень B.

4. 
   На что влияет начальная численность хищников и жертв?
   

Ответ:

5. 
   Подберите значения коэффициентов, при которых модель становится неадекватна.
   

Ответ:

bN =

bZ =

Уровень C.

6. 
   Установите значения коэффициентов и . Вставьте в отчёт график, который вы увидели:
   

Как вы можете объяснить это с точки зрения биологии?

Ответ:

7. 
   Установите значения коэффициента . Найдите экспериментально наибольшее значения коэффициента b_Z (с точностью 0,001), при котором к 25 году щуки вымирают, а численность карасей достигает предельно возможного значения.
   

Ответ:

bZ =

Как вы можете объяснить это с точки зрения биологии?

Ответ:

Практическая работа № 11а.

Модель «две популяции»

Для выполнения работы откройте файл-заготовку ДвеПопуляции.xls.

Белки и бурундуки живут в одном лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая изменение численности двух популяций, имеет вид:



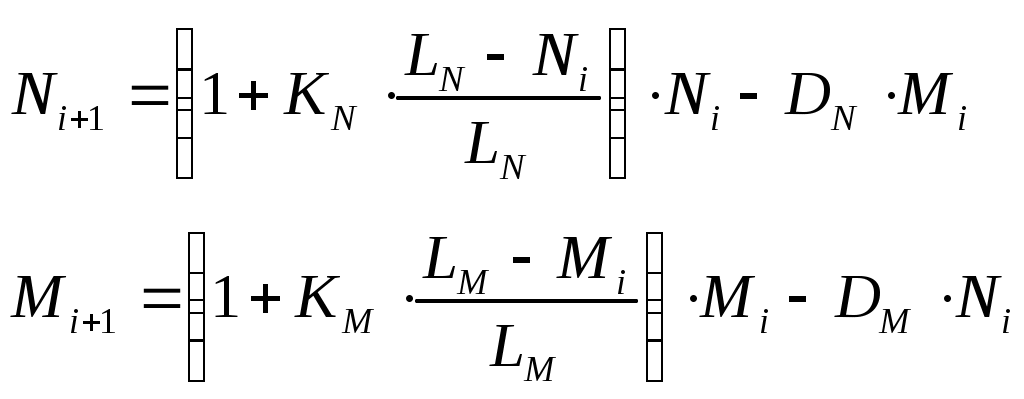
Здесь и – численность белок и бурундуков; и – их максимальные численности; и – коэффициенты прироста; и – коэффициенты взаимного влияния.

Объясните, на основании каких предположений была построена эта модель.

Ответ:

Выполните моделирование изменения численности двух популяций в течение 30 периодов при , , , , и .

Уровень A.

1. 
   Постройте графики изменения численности обеих популяций на одном поле.
   

2. 
   Является ли эта модель системной? Почему?
   

Ответ:

3. 
   Какова численность белок и бурундуков в состоянии равновесия?
   

Ответ:

4. 
   Что влияет на состояние равновесия, коэффициенты модели или начальная численность?
   

Ответ:

5. 
   На что влияет начальная численность животных?
   

Ответ:

Уровень B.

6. 
   При каком значении коэффициента через 30 лет останется 30 бурундуков? (используйте подбор параметра).
   

Ответ:

DM =

7. 
   Сколько тогда будет белок?
   

M =

8. 
   Найдите какие-нибудь значения коэффициента , при котором модель становится неадекватна. Почему вы так считаете?
   

Ответ:

DM =

Уровень C.

9. 
   *Предложите аналогичную модель взаимного влияния трех видов.
   

Ответ:

6. 
   Саморегуляция

Для выполнения работы откройте файл-заготовку Саморегуляция.xls.

Биологи выяснили, что для каждого вида животных существует некоторая минимальная численность популяции, которая необходима для выживания этой колонии. Это может быть одна пара животных (например, для ондатр) или даже тысячи особей (для американских почтовых голубей). Если количество животных становится меньше этого минимального значения, популяция вымирает. Для этого случая предложена следующая модель изменения численности:

, (*)

Эта модель отличатся от модели ограниченного роста только дополнительным множителем , где и – некоторые числа (параметры), смысл которых вам предстоит выяснить.

Уровень A.

1. 
   Выполните моделирование для 30 периодов при следующих значениях параметров модели:
   

Постройте на одном графике кривые, показывающие изменение численности по классической модели ограниченного роста и по модели (*).

Сделайте выводы и опишите, в чём проявляется саморегуляция для этих моделей.

Ответ:

2. 
   Постройте аналогичные графики для F = 500:
   

Сделайте вывод о том, как коэффициент F на саморегуляцию.

3. 
   Через 10 периодов в результате изменения природных условия число животных уменьшилось до 400 (то есть, ). Используйте значение F = 500. Выполните моделирование при этих условиях и постройте графики:
   

Опишите, чем отличается поведение двух сравниваемых моделей.

.

Как влияет изменение F на переходные процессы?

Уровень B.

4. 
   Повторите моделирование при и постройте графики:
   

Cделайте выводы:

Уровень C.

5. 
   Экспериментируя с моделями, найдите минимальную численность популяции , при которой она выживает в соответствии с моделью (*).
   

Ответ:

6. 
   Сделайте выводы о смысле коэффициента в модели (*).
   

Ответ:

7. 
   Сравните свойства саморегуляции для модели ограниченного роста и модели (*).
   

Ответ:

6. 
   Методы Монте-Карло

Уровень А.

1. 
   Используя метод Монте-Карло, приближённо определите значение числа  (см. § 12 учебника). Запишите в таблицу полученные результаты при различных значениях N:
   

N	100	1000	10000	100000	1000000
Результат ( )
Ошибка , %

Относительная ошибка в процентах вычисляется по формуле

,

где  = 3,1415926… и – приближённое значение числа , полученное в результате моделирования.

Уровень B.

2. 
   Не используя значение , с помощью метода Монте-Карло вычислите площади кругов различного диаметра:
   

   R	1	2	3	4	5
   S

3. 
   С помощью электронных таблиц постройте по этим данным зависимость S от R.
   
4. 
   Используя линию тренда, подберите функцию, которая лучше всего соответствует этой зависимости.
   

Ответ:

5. 
   Сравните эту функцию с известной вам формулой площади круга. Сделайте выводы.
   

Выводы:

Уровень C.

6. 
   Не используя значение , с помощью метода Монте-Карло вычислите объёмы шаров различного диаметра:
   

   R	1	2	3	4	5
   V

7. 
   С помощью электронных таблиц постройте по этим данным зависимость V от R.
   
8. 
   Используя линию тренда, подберите функцию, которая лучше всего соответствует этой зависимости.
   

Ответ:

9. 
   Сравните эту функцию с известной вам формулой объёма шара. Сделайте выводы.
   

Выводы:

6. 
   Системы массового обслуживания

Для моделирования обслуживания клиентов в банке предложена следующая модель:

• 
  за 1 минуту в банк входит случайное число клиентов, от 0 до (распределение равномерное);
  
• 
  на обслуживание клиентов требуется от до минут; время обслуживания определяется для каждой рабочей минуты случайным образом (распределение равномерное);
  
• 
  моделирование выполняется для интервала времени , равного 8-часам (рабочая смена).
  
• 
  число клиентов, находящихся в помещении банка, вычисляется по формуле
  

где – количество клиентов, вошедших за -ую минуту, а – количество клиентов, обслуженных за это время;

• 
  если кассир обслуживает клиента за минут, то можно считать, что за 1 минуту он сделает часть работы, равную ; если предположить, что скорость работы кассиров одинакова, то касс за 1 минуту обслужат клиентов;
  
• 
  если считать, что клиентов равномерно распределяются по кассам, так что средняя длина очереди равна , а среднее время ожидания в течение этой минуты равно
  

• 
  достаточным считается число касс, при которых среднее время ожидания превышает установленный предел не более, чем 5% рабочего времени в течение дня.
  

Используя эту вероятностную модель работы банка, напишите программу, с помощью которой определите минимальное необходимое количество касс при следующих исходных данных:

, , , .

http://kpolyakov.spb.ru