Шманева Л.В. Логика к в понятиях и терминах. Московский ФинансовоЮридический Университет мфюа

• Название: Московский ФинансовоЮридический Университет мфюа
• Дата: 24.01.2018
• Размер: 310.51 Kb.
• Имя файла: Шманева Л.В. Логика к в понятиях и терминах .docx
• Тип: Документы; #35052
• страница: 4 из 5

УМОЗАКЛЮЧЕНИЕ

УМОЗАКЛЮЧЕНИЕ — мыслительный процесс, в котором из одного или нескольких суждений, называемых посылками, выводится новое суждение, называемое следствием или заключением. Различают дедуктивные и недедуктивные умозаключения.

ДЕДУКТИВНОЕ УМОЗАКЛЮЧЕНИЕ - умозаключение, в котором из истинных посылок с необходимостью следует истинный вывод. Причем, как правило, в этом случае посылки умозаключения по степени общности превосходят заключение (непосредственные умозаключения, категорический силлогизм и его производные, условные, разделительные и условно-разделительные умозаключения).

НЕДЕДУКТИВНОЕ УМОЗАКЛЮЧЕНИЕ - умозаключение, имеющее такие связи между посылками, которые не гарантируют истинности заключения при истинных посылках (индуктивные умозаключения, умозаключения по аналогии).

ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ - это предложение, которое не может быть ложным, если оно выводится из истинных посылок. Другими словами, из посылок А₁, А₂, А₃, ..., А_n логически следует высказывание В, если это В истинно при истинности А₁, А₂, А₃, ..., А_n, или: высказывание В является логическим следованием из высказывания А, если импликация А → В является тождественно истинной формулой.

НЕПОСРЕДСТВЕННОЕ УМОЗАКЛЮЧЕНИЕ – умозаключение, в котором вывод строится на основе лишь одной посылки. К таким умозаключениям относят превращение, обращение, противопоставление предикату, умозаключение по логическому квадрату.

ПРЕВРАЩЕНИЕ — умозаключение, при котором изменяется качество посылки при одновременной замене предиката на противоречащий ему термин. Количественная характеристика суждения не меняется. Общая схема при этом такова:

(Все/Некоторые) S есть (не есть) Р →

(Все/Некоторые) S не есть (есть) не-Р.

ОБРАЩЕНИЕ — умозаключение, при котором происходит замена субъекта предикатом, а предиката — субъектом при сохранении качества суждения. Количественная характеристика заключения может быть иной по сравнению с количественной характеристикой посылки. Это зависит от распределенности терминов в исходном суждении; в случае когда термины посылки одновременно распределены или одновременно не распределены, количественные характеристики посылки и заключения совпадают. Частноотрицательное суждение не обращается. Общая схема обращения такова:

(Все/Некоторые) S есть (не есть) Р →

(?) Р есть (не есть) S.

ПРОТИВОПОСТАВЛЕНИЕ ПРЕДИКАТУ - умозаключение, в котором субъектом заключения является термин, противоречащий предикату, а предикатом — субъект посылки. Причем, посылка и заключение отличаются друг от друга качественной характеристикой. Частно-утвердительное суждение не противопоставляется предикату- Общая схема этого непосредственного умозаключения такова:

(Все/Некоторые) S есть (не есть) Р →

(?) не-Р не есть (есть) S.

УМОЗАКЛЮЧЕНИЕ ПО ЛОГИЧЕСКОМУ квадрату — умозаключение, которое строится на основе связи между суждениями, учитывающей их отношения по истинности (см. Логический квадрат)

КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ - умозаключение, в котором из двух категорических суждений выводится третье категорическое суждение, термины которого связаны определенным отношением с термином, общим для обеих посылок. Этот термин носит название среднего (обозначается буквой М). Субъект вывода называют меньшим термином (S), предикат вывода — большим термином (Р). При этом посылка, содержащая больший термин, называется большей, а посылка, содержащая меньший термин, — меньшей. Логическая форма силлогизма имеет следующий вид:

Все М суть Р.

Все S суть М.

Все S суть Р.

ОБЩИЕ ПРАВИЛА СИЛЛОГИЗМА - правила, распространяющиеся на все фигуры силлогизма. Выделяют две группы правил: правила терминов и правила посылок.

Правила т е р м и но в: 1) терминов должно быть в силлогизме только три; 2) средний термин должен быть распределен хотя бы в одной из посылок; 3) термин, не распределенный в посылке, не может быть распределен в выводе.

Правила п о с ы л о к. 1) из двух отрицательных, равно как и частных, посылок нельзя сделать никакго заключения; 2) если одна из посылок является отрицательным или частным суждением, то и заключение должно быть, соответственно, отрицательным или частным суждением.

ФИГУРА СИЛЛОГИЗМА - разновидность силлогизма в зависимости от местоположения среднего термина в посылках. Схематически эти фигуры можно изобразить так: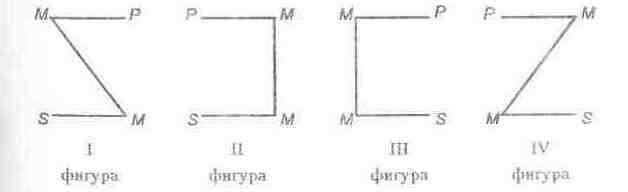



Каждая из фигур силлогизма имеет свои правила:

для I фигуры — большая посылка должна быть общей, а меньшая — утвердительной;

для II фигуры — большая посылка должна быть общей, а одна из посылок — отрицательным суждением;

для III фигуры — меньшая посылка должна быть утвердительным, а заключение — частным суждениями;

для VI фигуры — вывод всегда частное суждение. Если большая посылка — утвердительное суждение, то меньшая должна быть общим суждением. Если же одна из посылок — отрицательная, то большая посылка должна быть общей.

МОДУСЫ СИЛЛОГИЗМА — разновидность силлогизма в зависимости от количественной и качественной характеристик суждений, входящих в его состав. Каждая фигура силлогизма имеет свои правильные модусы:

I фигура - ААА, ЕАЕ, АII, ЕIO; II фигура - ЕAЕ, AЕЕ, ЕIO, AOО; III фигура - AАI, IАI, АII, ЕАО, ОАО, ЕIO; IV фигура - ААI, AЕЕ, IАI, ЕАО, ЕIO.

ЭНТИМЕМА — сокращенный категорический силлогизм, в котором пропущена одна из посылок или отсутствует заключение.

ПОЛИСИЛЛОГИЗМ — сложный силлогизм, состоящий из двух или более простых категорических силлогизмов, связанных между собой таким образом, что заключение каждого предыдущего силлогизма становится посылкой другого силлогизма.

Общая схема полисиллогизма, состоящего из двух простых, может быть такой:

Все А суть В.

Все С суть А.

Все С суть В.

Все D суть С.

Все D суть В

— прогрессивный полисиллогизм.

Может быть и другая схема:

Все A суть В.

Все В суть С.

Все А суть С.

Все С суть D.

Все А суть D.

— регрессивный полисиллогизм.

СОРИТ — сокращенный полисиллогизм, в котором пропущены заключение предшествующих силлогизмов и одна из посылок последующего силлогизма. Так же, как и полисиллогизм, сорит имеет две схемы:

Все А суть В.

Все С суть А.

Все D суть С.

Все D суть В.

— прогрессивный сорит;

Все А суть B.

Все В суть С.

Все С суть D.

Все А суть D.

— регрессивный сорит.

ЭПИХЕЙРЕМА — сокращенный и одновременно сложный силлогизм, посылки которого представляют собой энтимемы.

ЧИСТО УСЛОВНОЕ УМОЗАКЛЮЧЕНИЕ - умозаключение, посылки и заключение которого являются условными суждениями. Логическая структура такого умозаключения может иметь, например, такой вид:

р → q, q → l

p → l

КОНТРАПОЗИЦИЯ ПРОСТАЯ - условное умозаключение, логическая форма которого такова:

A→ B

ך B → ך A

КОНТРАПОЗИЦИЯ СЛОЖНАЯ - условное умозаключение, имеющее следующую форму:

(А В) → С

(А ךС) – ך B

ИМПОРТАЦИЯ — условное умозаключение, логическая схема которого:

А → (В → С)

(А В) → С

ЭКСПОРТАЦИЯ — условное умозаключение, логическая форма которого имеет следующий вид:

(А В) → С

А → (В → С)

УСЛОВНО-КАТЕГОРИЧЕСКОЕ УМОЗАКЛЮЧЕНИЕ — умозаключение, одна из посылок которого условное, а вторая — категорическое суждение. Это умозаключение имеет два правильных и два вероятных модуса. Структура правильных модусов:

1) утверждающий модус (modus ропепs)

p → q, p

q

2) отрицающий модус (modustоllепs)

p → q, ך q

ך p

Структура вероятностных (неправильных) модусов:

p → q, q p → q, ךp

p ךq

ЧИСТО-РАЗДЕЛИТЕЛЬНОЕ УМОЗАКЛЮЧЕНИЕ — умозаключение, в котором посылки и заключение являются разделительными суждениями. Его логическая структура может иметь следующий вид:

pvq, q ≡ q₁vq₂

p v q₁ v q₂

РАЗДЕЛИТЕЛЬНО-КАТЕГОРИЧЕСКОЕ УМОЗАКЛЮЧЕНИЕ — умозаключение, где одна из посылок — разделительное суждение, а вторая — категорическое. Оно имеет два модуса:

I модус — утверждающе-отрицающй (modus ропепdotollens), схема которого такова:

pvq, p pvq, q

ך q ךp

Этот модус является правильным только для строгой дизъюнкции;

II модус — отрицающе-утверждающий (modustollendo ропепs), схема которого:

pvq, pך pvq, ךq

q p

Этот модус является правильным как для строгой, так и для нестрогой дизъюнкций.

УСЛОВНО-РАЗДЕЛИТЕЛЬНОЕ УМОЗАКЛЮЧЕНИЕ — умозаключение, в котором одна из посылок — разделительное суждение, а вторая является совокупностью условных суждений. Различают: 1) дилеммы, 2) трилеммы и 3) полилеммы:

1) дилемма — умозаключение, где одна из посылок является разделительным суждением с двумя альтернативами, а вторая состоит из одного или двух условных суждений. Различают дилеммы простые и сложные, конструктивные и деструктивные. Формы правильных дилемм основных видов можно представить следующей таблицей:



2) трилемма — умозаключение, в котором одна из посылок — разделительное суждение с тремя альтернативами, а вторая содержит три условных посылки. Ее структура может иметь такой, например, вид:

p → q, l → m, k → n;

pvlvk ,

q v m v n

3) полилемма — условно-разделительное умозаключение, где одна из посылок — разделительное суждение с более, чем тремя вариантами выбора, а вторая состоит из более, чем трех условных суждений.

ИНДУКТИВНОЕ УМОЗАКЛЮЧЕНИЕ - умозаключение, в котором заключение о свойствах каждого элемента некоторого множества делается на основании изучения свойств его отдельных элементов. Различают:

1) индукцию математическую, 2) полную и 3) неполную:

1) индукция математическая — один из приемов доказательства общих положений в математике. Состоит в следующем: если известно (установлено, доказано), что некоторый объект какого-либо множества, состоящего из п элементов, обладает свойством Р (1), а также, что предположение о том, что если из того, что К элементов данного множества обладают свойством Р, следует, что и К + 1 элемент имеет указанное свойство, оказывается верным (2), то из (1) и (2) заключают, что все п элементов данного множества обладают свойством Р;

2) индукция полная — умозаключение, в котором общий вывод о свойствах элементов некоторого класса делается на основании изучения каждого элемента данного класса;

3) индукция неполная — умозаключение, в котором заключение о том, что некоторое свойство Р принадлежит каждому элементу какого-либо множества, делается исходя из того, что установлен факт принадлежности свойства Р лишь некоторым элементам данного множества. Различают: индукцию через простое перечисление (популярную индукцию) и научную индукцию.

ИНДУКЦИЯ ЧЕРЕЗ ПРОСТОЕ ПЕРЕЧИСЛЕНИЕ (ПОПУЛЯРНАЯ) — неполная индукция, при которой общее заключение о принадлежности некоторого свойства всем элементам данного множества делается на том основании, что этот признак (свойство) обнаруживается у ряда совершенно произвольно взятых элементов множества.

НАУЧНАЯ ИНДУКЦИЯ - неполная индукция, при которой общее заключение о принадлежности некоторого свойства каждому элементу данного множества делается на основе установления с помощью каких-либо специальных (научных) методов принадлежности этого свойства части элементов исследуемого множества. Различают индукцию через отбор и индукцию на основе установления причинно-следственных связей.

ИНДУКЦИЯ ЧЕРЕЗ ОТБОР - неполная индукция, при которой вывод о принадлежности некоторого свойства каждому элементу какого-либо множества делается на основании изучения планомерно отобранных по каким-то признакам элементов множества.

ИНДУКЦИЯ НА ОСНОВЕ УСТАНОВЛЕНИЯ ПРИЧИННО-СЛЕДСТВЕННЫХ СВЯЗЕЙ - этот вид научной индукции опирается на специальные методы установления причинных связей: 1) метод сходства, 2) метод различия, 3) метод сопутствующих изменений и 4) метод остатков:

1) метод сходства — один из методов установления причинно-следственной связи, схема которого такова:



Вывод: вероятно, что А есть причина а;

2) метод различия — сводится к тому, что если предшествующие обстоятельства различаются только одним из них, то, вероятно, что оно и является причиной наблюдаемого явления. Схема этого метода такова: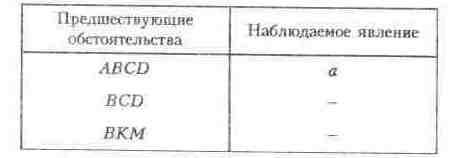



Вывод: вероятно, что А есть причина а;

3) метод сопутствующих изменений — заключается в том, что если изменение предшествующего обстоятельства ведет к изменению наблюдаемого явления при неизменности остальных предшествующих обстоятельств, то именно оно и является причиной наблюдаемого явления;

4) метод остатков — суть этого метода в следующем. Пусть изучаемому сложному явлению аbcde предшествуют обстоятельства АВСDЕ, из которых А есть причина а, В — причина b, С — причина с, а D — причина d. Тогда можно предположить, что причиной е является обстоятельство Е.

УМОЗАКЛЮЧЕНИЕ ПО АНАЛОГИИ (АНАЛОГИЯ) — индуктивное умозаключение, при котором на основе сходства двух объектов по каким-либо параметрам делается вывод об их сходстве по другим параметрам. Различают аналогию свойств и аналогию отношений, а также строгую и нестрогую аналогии.

АНАЛОГИЯ ОТНОШЕНИЙ - в этом умозаключении речь идет об отношениях между предметами. И если некоторые отношения имеют какие-либо общие (сходные) свойства, то обнаружение некоторого отличного от этой совокупности свойства у одного отношения дает основания сделать вывод о возможности принадлежности этого свойства и другому отношению.

АНАЛОГИЯ СВОЙСТВ - здесь сравниваются два предмета (два класса предметов), а переносимыми признаками являются свойства этих предметов (классов).

АНАЛОГИЯ НЕСТРОГАЯ — здесь связь между сходными и переносимыми признаками не является необходимой. Вывод является вероятностным.

АНАЛОГИЯ СТРОГАЯ — отличается тем, что в этом случае имеющиеся сходные признаки необходимо связаны с переносимым признаком. Вывод в этом случае является достоверным.