Курсовая Работа Микропроцессорная техника. БЗС1901 Радаев А.О. Курсовая работа. Московский технический университет связи и информатики

Название	Московский технический университет связи и информатики
Анкор	Курсовая Работа Микропроцессорная техника
Дата	03.05.2022
Размер	1.04 Mb.
Формат файла
Имя файла	БЗС1901 Радаев А.О. Курсовая работа.docx
Тип	Курсовая #510370

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение высшего образования
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

Кафедра Многоканальные телекоммуникационные системы

Курсовая работа

Выполнил: студент группы БЗС1901

Радаев А.О.

Проверил: С.С. Шаврин

Москва 2022

1 Исходные данные

На рисунке 1 показано задание на проектирование КИХ-фильтра.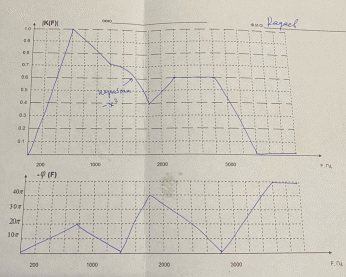

Рисунок 1 - Задание на проектирование в виде амплитудно-частотной и фазо-частотной характеристик

Порядок фильтра n = 79.
2 Процесс расчета КИХ-фильтра

Найдем уравнения для каждой прямой, аппроксимируя заданные АЧХ и ФЧХ: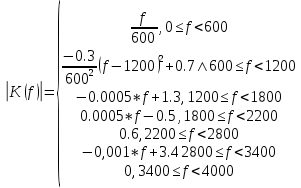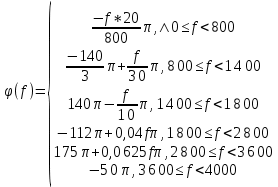

Результаты аппроксимации 41 точек показаны в табл. 1.

Таблица 1 Аппроксимация АЧХ и ФЧХ

n	f	𝐾(f)	𝜑(f)
0	0	0	0
1	100	0,16666	-7,85398
2	200	0,33333	-15,70796
3	300	0,5	-23,56194
4	400	0,66666	-31,41593
5	500	0,83333	-39,26991
6	600	1	-47,12389
7	700	0,95	-54,97787
8	800	0,9	-62,83185
9	900	0,85	-52,35988
10	1000	0,8	-41,8879
11	1100	0,75	-31,41593
12	1200	0,7	-20,94395
13	1300	0,69166	-10,47198
14	1400	0,66666	0
15	1500	0,625	-31,41593
16	1600	0,56666	-62,83185
17	1700	0,49166	-94,24778
18	1800	0,4	-125,66371
19	1900	0,45	-113,09734
20	2000	0,5	-100,53096
21	2100	0,55	-87,96459
22	2200	0,6	-75,39822
23	2300	0,6	-62,83185
24	2400	0,6	-50,26548
25	2500	0,6	-37,69911
26	2600	0,6	-25,13274
27	2700	0,6	-12,56637
28	2800	0,6	0
29	2900	0,5	-19,63495
30	3000	0,4	-39,26991
31	3100	0,3	-58,90486
32	3200	0,2	-78,53982
33	3300	0,1	-98,17477
34	3400	0	-117,80972
35	3500	0	-137,44468
36	3600	0	-157,07963
37	3700	0	-157,07963
38	3800	0	-157,07963
39	3900	0	-157,07963
40	4000	0	-157,07963

Постоим график действительной и мнимой части от АЧХ и ФЧХ, использовав формулу: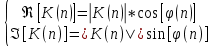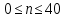

В таблице 2 представлены значения действительной и мнимой частей.

Таблица 2 Значения мнимой и действительной частей АЧХ и ФЧХ

n	f	𝑅𝑒[𝐾(f)]	𝐼𝑚[𝐾(f)]
0	0	0,000000000	0,000000000
1	100	0,000000000	-0,166666667
2	200	-0,333333333	0,000000000
3	300	0,000000000	0,500000000
4	400	0,666666667	0,000000000
5	500	0,000000000	-0,833333333
6	600	-1,000000000	0,000000000
7	700	0,000000000	0,950000000
8	800	0,900000000	0,000000000
9	900	-0,425000000	-0,736121593
10	1000	-0,400000000	0,692820323
11	1100	0,750000000	0,000000000
12	1200	-0,350000000	-0,606217783
13	1300	-0,345833333	0,599000904
14	1400	0,666666667	0,000000000
15	1500	0,625000000	0,000000000
16	1600	0,566666667	0,000000000
17	1700	0,491666667	0,000000000
18	1800	0,400000000	0,000000000
19	1900	0,450000000	0,000000000
20	2000	0,500000000	0,000000000
21	2100	0,550000000	0,000000000
22	2200	0,600000000	0,000000000
23	2300	0,600000000	0,000000000
24	2400	0,600000000	0,000000000
25	2500	0,600000000	0,000000000
26	2600	0,600000000	0,000000000
27	2700	0,600000000	0,000000000
28	2800	0,600000000	0,000000000
29	2900	0,353553391	-0,353553391
30	3000	0,000000000	-0,400000000
31	3100	-0,212132034	-0,212132034
32	3200	-0,200000000	0,000000000
33	3300	-0,070710678	0,070710678
34	3400	0,000000000	0,000000000
35	3500	0,000000000	0,000000000
36	3600	0,000000000	0,000000000
37	3700	0,000000000	0,000000000
38	3800	0,000000000	0,000000000
39	3900	0,000000000	0,000000000
40	4000	0,000000000	0,000000000

Построим с помощью математического пакета MathLab график реальной части комплексного коэффициента передачи по полученным ранее точкам, а также график мнимой части КЧХ в диапазоне от 0 до Fд/2 (4000 Гц).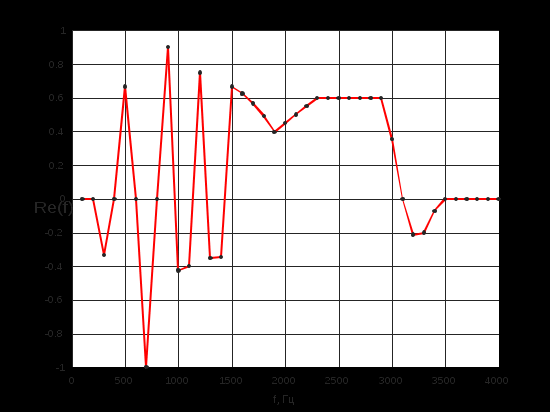

Рисунок 2 - Действительная часть КЧХ в диапазоне 0 ≤ 𝑓 < 𝐹_д/2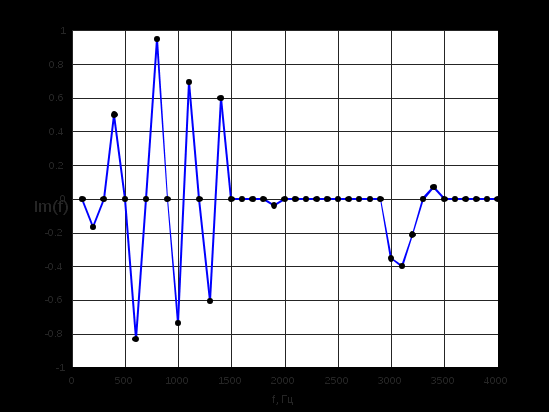

Рисунок 3 - Мнимая часть КЧХ в диапазоне 0 ≤ 𝑓 < 𝐹_д/2

Дополним полученные графики до полной частоты дискретизации (8000 Гц), отразив их зеркально. При отражении мнимой части необходимо также поменять знак на противоположный.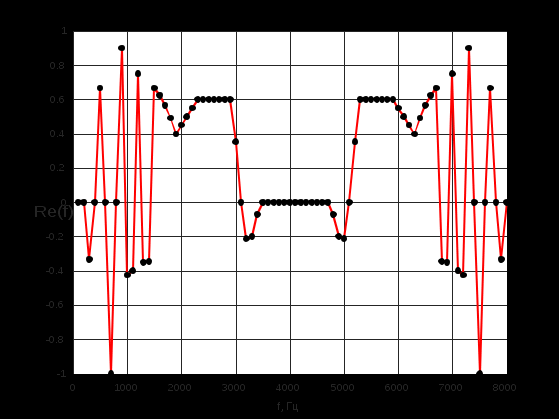

Рисунок 4 - Действительная часть КЧХ в диапазоне 0 ≤ 𝑓 < 𝐹д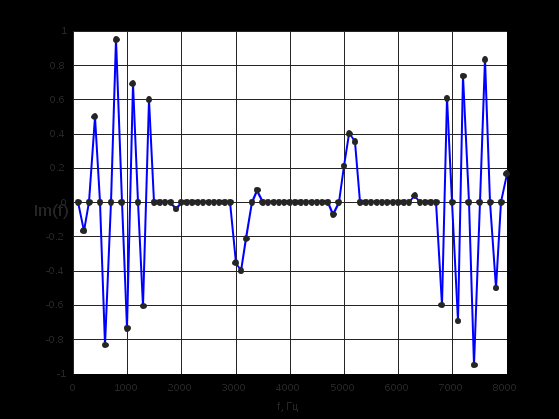

Рисунок 5 - Мнимая часть в диапазоне 0 ≤ 𝑓 < 𝐹д

3. Произведем обратное преобразование Фурье для нахождения импульсной характеристики КЧХ фильтра с помощью математического пакета MathLab:

% преобразование Фурье

% с приведением результатов вычисления

% отсчетов импульсной характеристики

% к формату, предназначенному для подключения

% к программе реализации цифрового фильтра

% на базе 16-разрядных процессоров (ADSP-2181)
re_spec = [];

im_spec = [];

for i=1:1:80

re_spec = [re_spec, 0];

im_spec = [im_spec, 0];

end
for k=1:80

w=2.*%pi.*(k-1)./80;

x=0;

y=0;

for j=1:80

x=x+Re3(j).*cos(w.*(j-1))+Im3(j).*sin(w.*(j-1));

y=y-Re3(j).*sin(w.*(j-1))+Im3(j).*cos(w.*(j-1));

end

re_spec(k)=x./80.*32768;

im_spec(k)=y./80.*32768;

end
N =0:1:79;

scf(5);

plot(N,re_spec);

Результаты расчета отсчетов импульсной характеристики фильтрa по рассматриваемому примеру представлены в виде графика на рис. 6.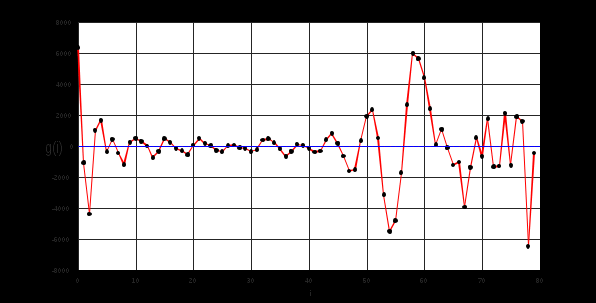

Рисунок 6 - Импульсная характеристика фильтра

4. Разработка программы на языке ассемблера процессора ADSP-2181.

Реализация программы фильтра, работающего в реальном времени, потребует ликвидации процедуры зацикливания программы и разбиения программы на 3 части. Одна ее часть включена в общую программу в раздел объявления и инициализации переменных. Вторая часть в основную программу, а третья часть оформлена как подпрограмма, ассоциированная с таймерным прерыванием.

.SECTION/DM vars;

.var/circ signal[80] = 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,

0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,

0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,

0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;

.SECTION/PM varsp;

.var/circ impr[80] = "g_re.dat";

.SECTION/PM program;
jump start; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;

rti; rti; rti; rti;
start: i4 = impr;

l4 = length(impr);

i0 = signal;

l0 = length(signal);

m4 = 1;

m0 = 0;

m1 = 1;

my0 = pm(i4,m4);
do out until forever;

mx0 = IO(0);

dm(i0,m1)= mx0, mr = 0;
cntr = 78;

do filter until ce;

filter: mr = mr + mx0 * my0 (ss), mx0 = dm(i0,m1), my0 = pm(i4,m4);

mr = mr + mx0 * my0(ss), mx0 = dm(i0,m0), my0 = pm(i4,m4);

mr = mr + mx0 * my0(ss), my0 = pm(i4,m4);

mr = mr(rnd);

if mv sat mr;
out: IO(1) = mr1;

jump start;

Правильность программы проверим, подав на вход фильтра единичный импульс с максимальной амплитудой, т.е. число 32767. На выходе фильтра получаем массив значений импульсной характеристики, значит, программа работает корректно.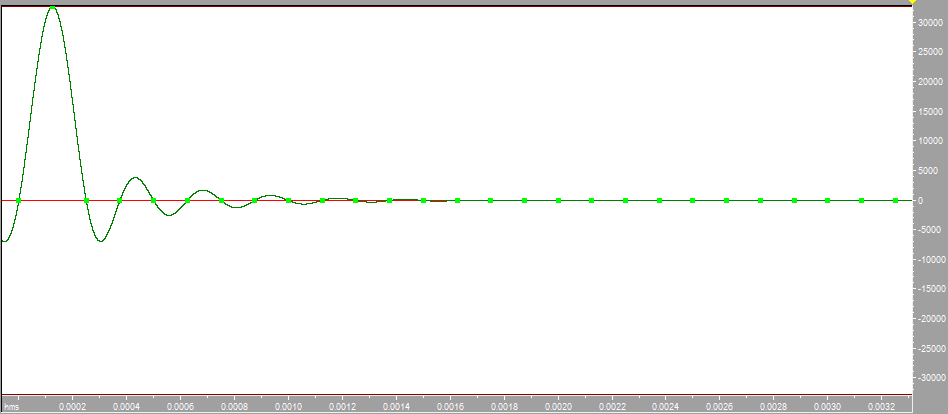

Рисунок 7 - Единичный импульс.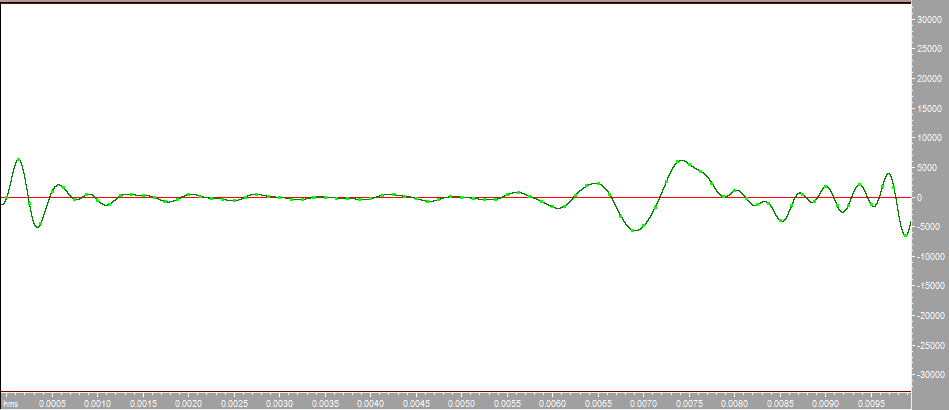

Рисунок 8 - Импульсная характеристика

5. Инвертируем нашу импульсную характеристику, зашумим и подадим на вход фильтра: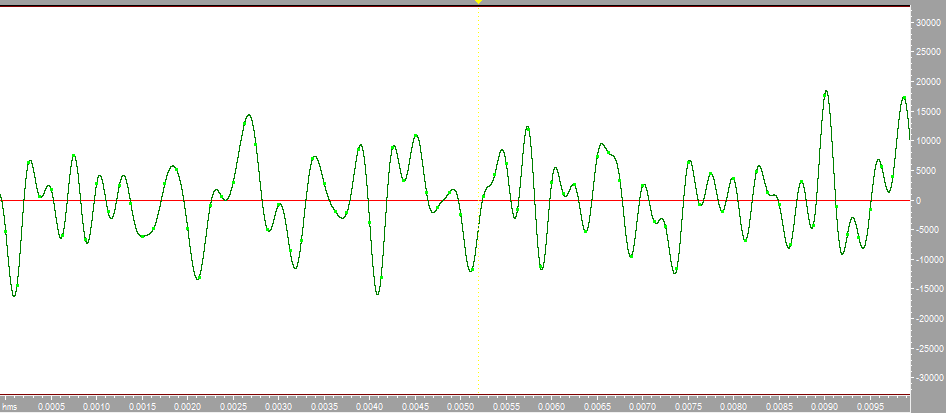

Рисунок 9 - Зашумленная импульсная характеристика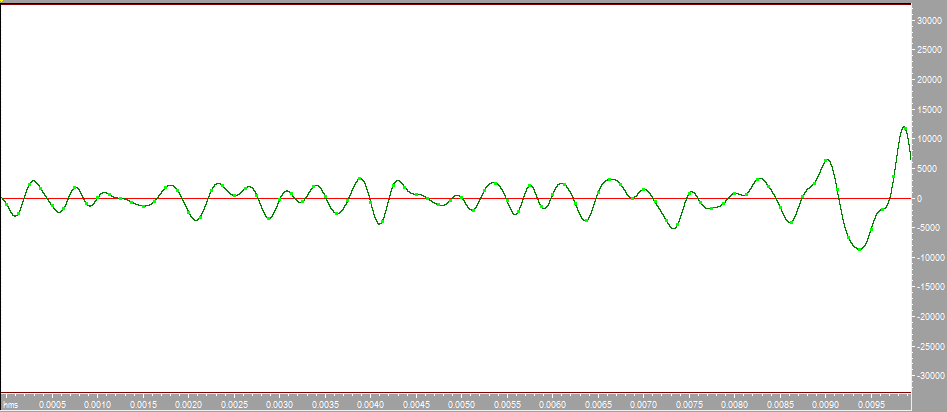

Рисунок 10 - Зашумленная импульсная характеристика на выходе фильтра

Исходя из рисунков видно, что фильтр справляется с шумами.

6. Для исследования АЧХ полученного цифрового фильтра в CoolEdit были сформированы синусоиды частотой 600 Гц, 1200 Гц, 1800 Гц, 2200 Гц, 2800 Гц, 3400 Гц и длительностью 0.1 с. Сигналы, полученные на выходе фильтра представлены ниже.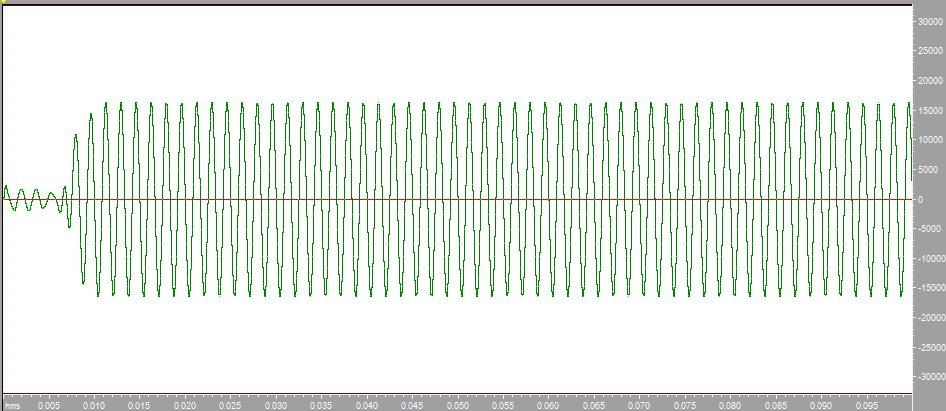

Рисунок 11- Синусоида с частотой 600Гц на выходе фильтра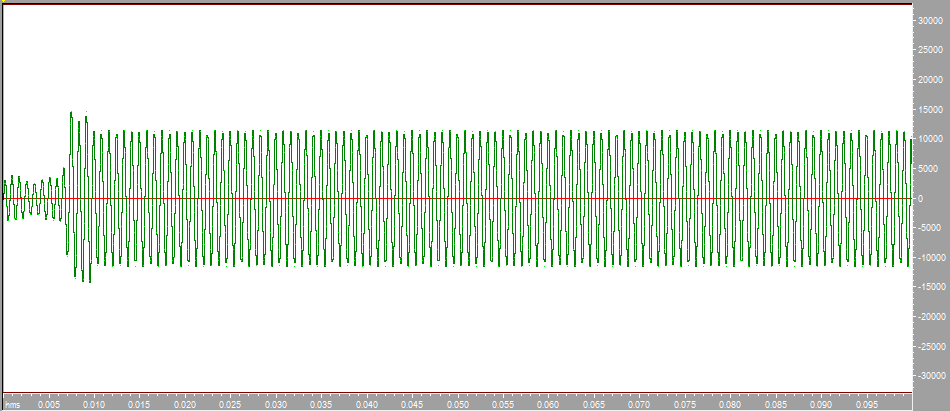

Рисунок 12 - Синусоида с частотой 1200Гц на выходе фильтра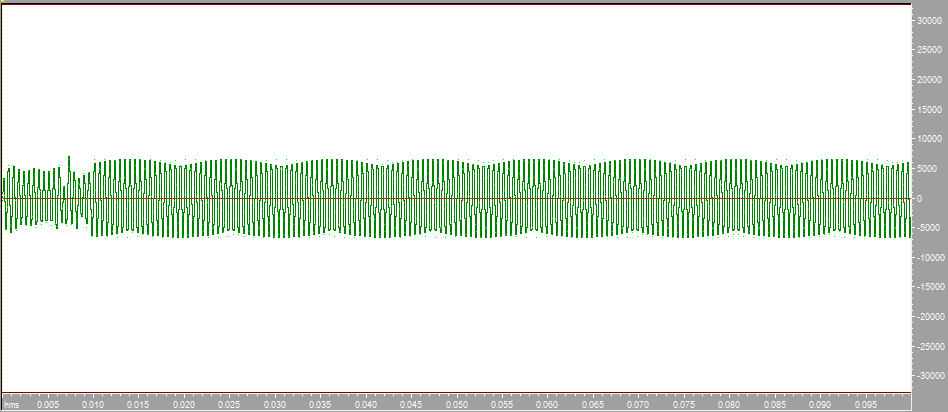

Рисунок 13 - Синусоида с частотой 1800Гц на выходе фильтра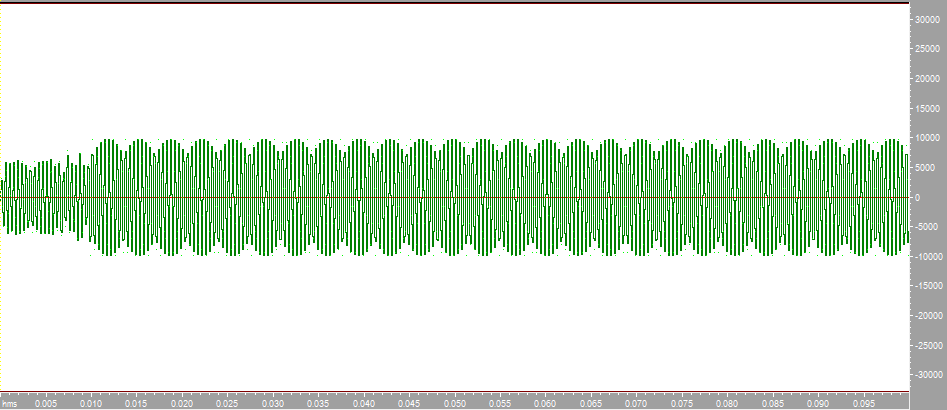

Рисунок 14 - Синусоида с частотой 2200Гц на выходе фильтра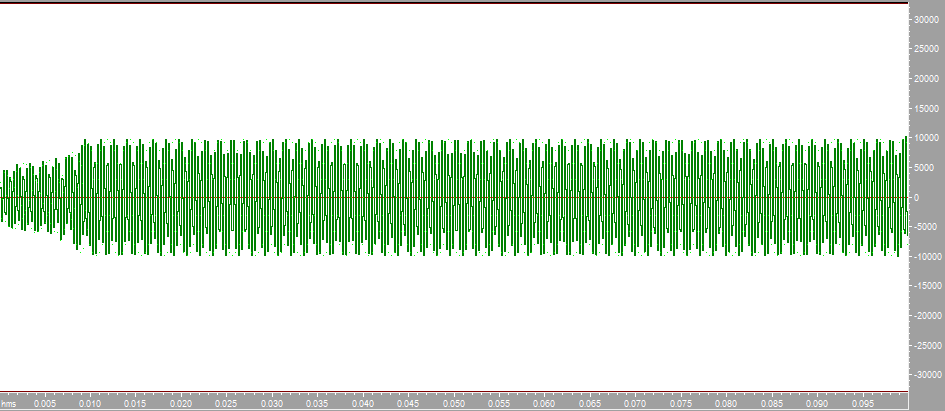

Рисунок 15 - Синусоида с частотой 2800Гц на выходе фильтра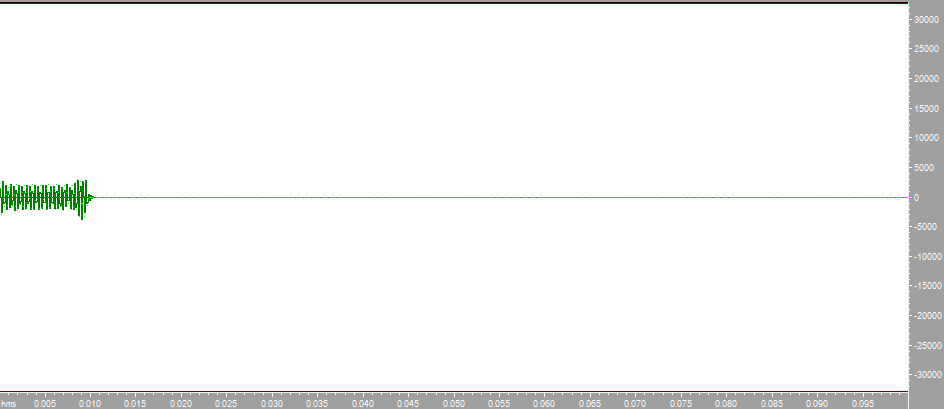

Рисунок 16 - Синусоида с частотой 3400Гц на выходе фильтр

Вывод:

В данной курсовой работе был разработан цифровой фильтр с КИХ на микропроцессоре ADSP2181. Расчетная импульсная характеристика совпадает с импульсной характеристикой полученной при подаче на вход программы единичного импульса. Также была проведена проверка АЧХ фильтра с помощью подачи синусойд с частотами в контрольных точках (значения АЧХ:1,0.6,0.2,0,0.4,0). Из полученных результатов можно сделать вывод что фильтр работает правильно.