МГТУ физика 3 семестр 1 задача. Разобранные ДЗ - Электростатика. Н. Э. Баумана электростатика разобранные задачи по физике 3 семестр Редактор Fozi icq 1860 Москва, 2002 Задача
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
Условие:Плоский диэлектрический конденсатор заряжен до разности потенциалов U и расстояние между обкладками равно d. Величина диэлектрической проницаемости между обкладками меняется по закону ε=f(у). Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу площади. d0/d=2/1, n=1. По результатам вычислений построить графически зависимости D(y), E(y), P(y). Решение:По теореме Гаусса Т.к. Определим поверхностную плотность связанных зарядов Поэтому Объёмная плотность связанных зарядов Для определения ёмкости вычислим напряжение на его обкладках 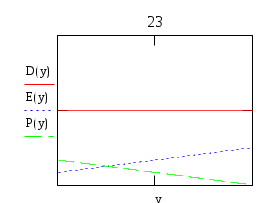 Поэтому Вариант 24Условие:Плоский диэлектрический конденсатор заряжен до разности потенциалов U и расстояние между обкладками равно d. Величина диэлектрической проницаемости между обкладками меняется по закону ε=f(у). Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу площади. 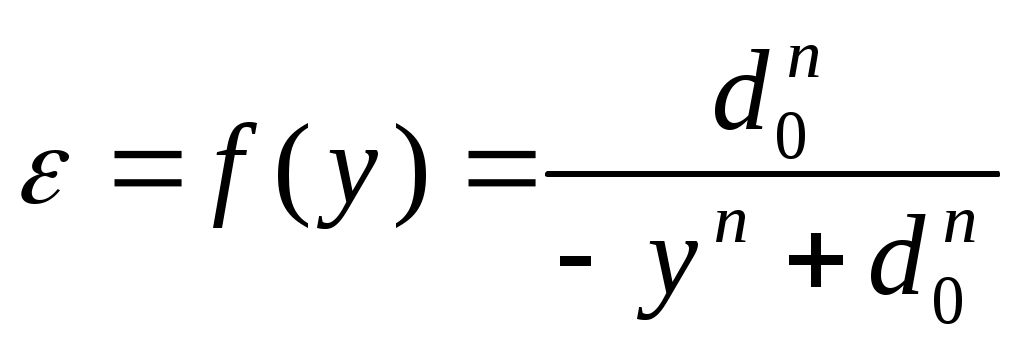 d0/d=3/1, n=2. По результатам вычислений построить графически зависимости D(y), E(y), P(y). Решение:По теореме Гаусса Т.к. Определим поверхностную плотность связанных зарядов Поэтому Объёмная плотность связанных зарядов Для определения ёмкости вычислим напряжение на его обкладках П 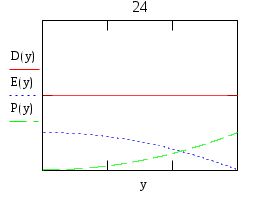 оэтому оэтому Вариант 25Условие:Плоский диэлектрический конденсатор заряжен до разности потенциалов U и расстояние между обкладками равно d. Величина диэлектрической проницаемости между обкладками меняется по закону ε=f(у). Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу площади. d0/d=3/1, n=1. По результатам вычислений построить графически зависимости D(y), E(y), P(y). Решение:По теореме Гаусса Т.к. Определим поверхностную плотность связанных зарядов Поэтому Объёмная плотность связанных зарядов Для определения ёмкости вычислим напряжение на его обкладках П 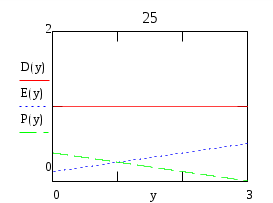 оэтому оэтому Вариант 26Условие:Плоский диэлектрический конденсатор заряжен до разности потенциалов U и расстояние между обкладками равно d. Величина диэлектрической проницаемости между обкладками меняется по закону ε=f(у). Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу площади. 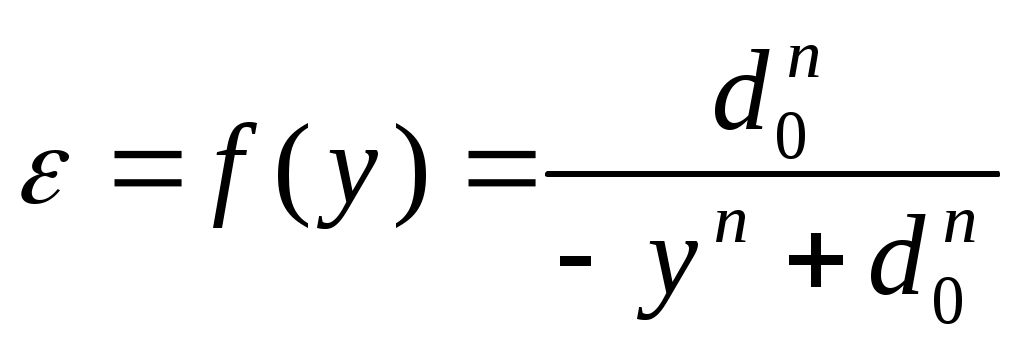 d0/d=3/1, n=2. По результатам вычислений построить графически зависимости D(y), E(y), P(y). Решение:По теореме Гаусса Т.к. Определим поверхностную плотность связанных зарядов Поэтому Объёмная плотность связанных зарядов Для определения ёмкости вычислим напряжение на его обкладках П 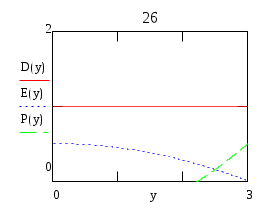 оэтому оэтому |
