Курсовая работа. записка. Н. Э. Баумана Факультет "Робототехники и комплексной автоматизации" Кафедра "Теории механизмов и машин" расчетнопояснительная записка
 Скачать 0.67 Mb.
|
|
1.3 Определение приведенных моментов. Для определения сил действующих на поршни детандера построена индикаторная диаграмма давления в цилиндрах детандера по заданным давлениям. Считая силу положительной, когда она совершает положительную работу (направление действия совпадает с направлением скорости приложения), а отрицательной – когда совершает отрицательную работу, строим график сил, действующих на поршни. Силы подсчитаны по формулам: F=P*π*d32/4 Масштаб графика сил построен в масштабе μF=0.0023 мм/кН Для определения приведенного момента Мпр использована формула Мпр=F*VqB*cos(FД^VqB), где так как векторы FД и VqB параллельны 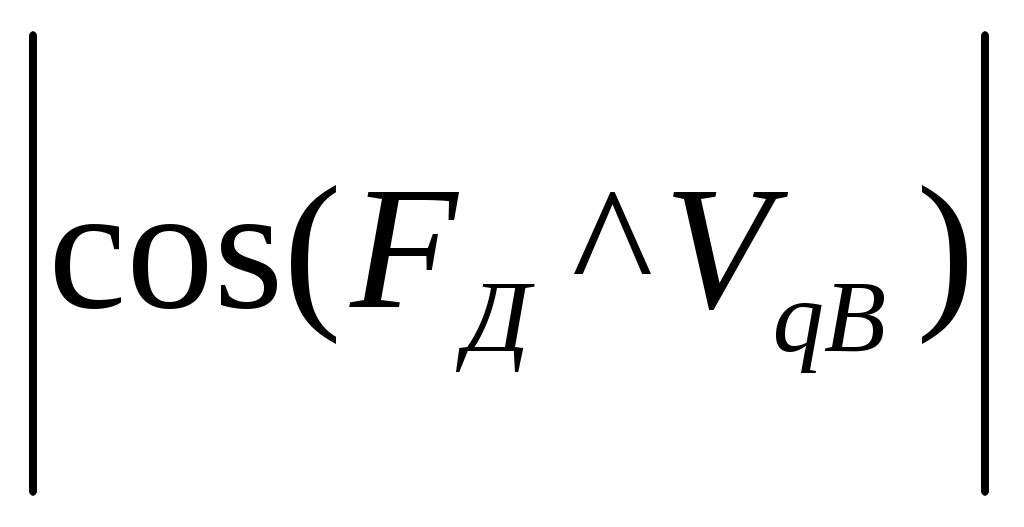 = 1. Результаты расчетов занесены в таблицу 1.2. Приведенные моменты  , и  ,  от сил тяжести G2, G3, G4, G5 звеньев 2, 3, 4, 5 пренебрежимо малы по сравнению с приведенным движущим моментом МДпр, поэтому не учитываются.    Суммарный приведенный момент от сил давления на поршнях M35пр является алгебраической суммой приведенного момента М3пр и М5пр. M35пр = М3пр + М5пр. Результаты расчетов занесены в таблицу 1.2. В масштабе μМ=0.025мм/кН*м2 построены графики приведенных моментов. Момент сопротивления найдет из равенства нулю работы за цикл (один оборот вала). Для этого проведено интегрирование графика суммарного приведенного момента M35пр и по найденной работе определен приведенный момент сопротивления. Мспр=1898 Н*м2 Суммарный приведенный момент от сил давления на поршни и сил сопротивления равен алгебраической сумме M∑пр = М3пр + М5пр+ Мспр. График получен из построенного ранее графика путем смещения оси на Мспр. Результаты расчетов помещены в таблицу 1.2. Таблица 1.2
1.4 Приведение масс звеньев механизма. Приведение масс выполнено на основе равенства кинетической энергии всех звеньев механизма и звена одномассовой динамической модели. В этом случае закон движения последней будет таким же, как и закон движения начального звена реального механизма. Приведенные моменты инерции звеньев второй группы определены по формулам J3пр = m3 * VqB2 J2пр = m2 * VqS22 + JS2 * U212 J5пр = m5 * VqC2 J4пр = m4 * VqS42 + JS4 * U412 Суммарный момент инерции второй группы звеньев JIIпр равен сумме приведенных моментов инерции звеньев. JIIпр = J2пр + J3пр + J4пр + J5пр Графики приведенных моментов инерции построены в масштабе μJ=193.8 мм/кг*м2. Результаты расчета занесены в таблицу 1.3. Таблица 1.3
1.5 Построение графика угловой скорости Определение закона движения звена приведения одномассной динамической модели. В первом приближении суммарный график приведенных моментов инерции второй группы звеньев принимаем за график кинетической энергии второй группы звеньев TII = f(f1 ), который построен в масштабе: µT= 2* µI /(w1cр )^2. Средняя угловая скорость подсчитывается по формуле: w1cр= π*n1/30 (здесь число оборотов n1 обязательно подставляется в об/мин). w1cр= 3.14*390/30= 40.84 рад/c. µT= 2*193,8/(40,84)^2= 0.232 мм/Дж. µT= 0.232 мм/Дж. Построим графическую зависимость TII = f(f1 ) в масштабе µT и пересчитаем ее в масштаб графика суммарной работы µА. Примем YTнач = 40мм. Опустив ось f1 на величину YTнач , получим ось f*1, относительно которой будет построен график суммарной кинетической энергии машинного агрегата TS= f(f1 ). Графическая зависимость угловой скорости w1= f(f**1 ), построенна относительно оси f**1 в масштабе µw= µА*w1cр*Iпр I_необх , мм/радc^(-1). Iпр I_необх = D TI_max / ((w1cр )^2)* d , кгм^2. D TI_max = YTI_max / µА , Дж. YTI_max = YTImax- YTImin = 44,25 мм. D TI_max = 44,25/ 0.0191 = 2316,75 Дж. Iпр I_ = 2316,75 / ((40,84)^2)*(1/28) = 38,89 кгм^2/рад^2. µw= 0,0191*40,84*40,84= 30,34 мм/радc^(-1). µw= 30,34 мм/радc^(-1). Yw1ср = w1cр* µw= 40,84*30,34= 1239мм. Yw1ср= 1239мм. 1.6 Определение углового ускорения звена приведения Угловое ускорение звена приведения определяем только для одной позиции ,которая задана углом f1 для силового расчета в таблице технического задания. Формула для расчета углового ускорения имеет вид: ei = MпрS i/ IпрS i – ((wi)^2/2*IпрS i)* dIпрS i/df1 MпрS i= f(f1 ) = 2918 Нм. IпрS i= Iпр I =38,89 кгм^2/рад^2. Ywi= Yw2= Yw1ср-YDw2= 1239-0= 1239 мм. wi= w2 = 40,84 рад/с. dIпрS i/df1= dIпр II/df1= (µf/ µI)*tgyk . tgyk= 0,23 dIпрS i/df1=(µf/ µI)*tgyk=( 38,2/ 093,8)*0,23= 0,045 кгм^2/рад. ei= e2= 2918/38,89–((40.84)^2/2*38,89)*0.045= 74,067 рад^2/с^2. e2= 74,067 рад^2/с^2. 2. Силовой расчет механизма. Для рассчитываемого положения механизма  Из первого листа находим для этого положения   Силы, действующие на поршень:  ,  Скорости и ускорения звеньев определены по построенным планам скоростей и ускорений. План скоростей построен в масштабе μV=10 мм/(м/с). План ускорений построен в масштабе μа=0,7 мм/(м/с2). Построение плана скоростей для точек механизма в заданном положении:             ω2 = ω4 = VBA/lAB = 1.829/0.396 = 4.62 рад/c     anA= ω12*lAO = 40.842*0.088 = 146.78 м/с2 aτA= ε1*lAO = 74.067*0.088 = 6.5 м/с2 aA= 146.92 м/с2 anA’= ω12*lAO = 40.842*0.088 = 146.78м/с2 aτA’= ε1*lAO = 74.067*0.088 = 6.5 м/с2 aA’= 146.92 м/с2 anBA = ω22*lAB = 4.622*0.396=8.45 м/с2 aτBA = 124.51 м/с2 aB = 63.3 м/с2 anB’A’ = ω22*lAB = 4.622*0.396=8.45 м/с2 aτB’A’ = 124.51 м/с2 aB’ = 94.69 м/с2 aS2 = 114.14 м/с2 aS4 = 120.49 м/с2 ε2 = aτВA / lBA = 124.51 / 0.396 = 314.42 рад/с2 ε4 = aτВ’A’ / lB’A’ = 124.51 / 0.396 = 314.42 рад/с2 Определение главных векторов и главных моментов сил инерции:        Определение сил тяжести звеньев:   Для первого звена масса не задана, значит, его весом пренебрегаем. Силовой расчет механизма: Запишем уравнение Даламбера для третьего звена:  Рассмотрим отдельно звено 2:  Так как звено находится в равновесии, то можем записать      Запишем уравнение Даламбера для группы звеньев 2-3:  В уравнении два неизвестных, значит его можно решить. Строим план сил в масштабе 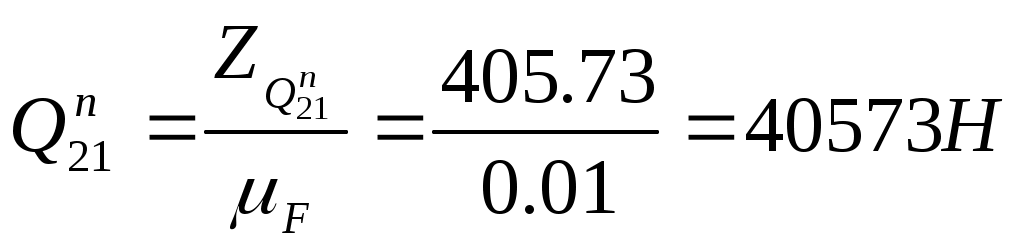    Теперь можно решить уравнение для звена 3:  Строим план сил в масштабе Из чертежа находим  Запишем уравнение Даламбера для пятого звена:  Рассмотрим отдельно звено 4: Так как звено находится в равновесии, то можем записать    -   Запишем уравнение Даламбера для группы звеньев 4-5:  В уравнении два неизвестных, значит его можно решить. Строим план сил в масштабе 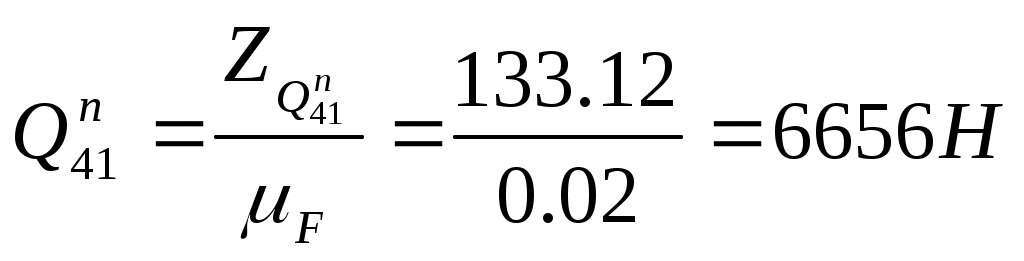    Теперь можно решить уравнение для звена 5:  Строим план сил в масштабе Из чертежа находим  Запишем уравнение Даламбера для звена 1:  Строим план сил в масштабе  Из чертежа находим  Для нахождения момента сопротивления запишем уравнение равновесия первого звена:      Вычислим разницу:  3. Проектирование цилиндрической зубчатой передачи и планетарного редуктора. 3.1 Проектирование зубчатой передачи. 3.1.1 Геометрический расчет зацепления. В основу методики расчета эвольвентных зубчатых передач внешнего зацепления положена система расчета диаметров окружностей вершин колес, при которой в зацеплении пары колес сохраняется стандартный зазор c*m. Расчет велся при свободном выборе межосевого расстояния. Были определены радиусы делительных окружностей колес  ,радиусы основных окружностей 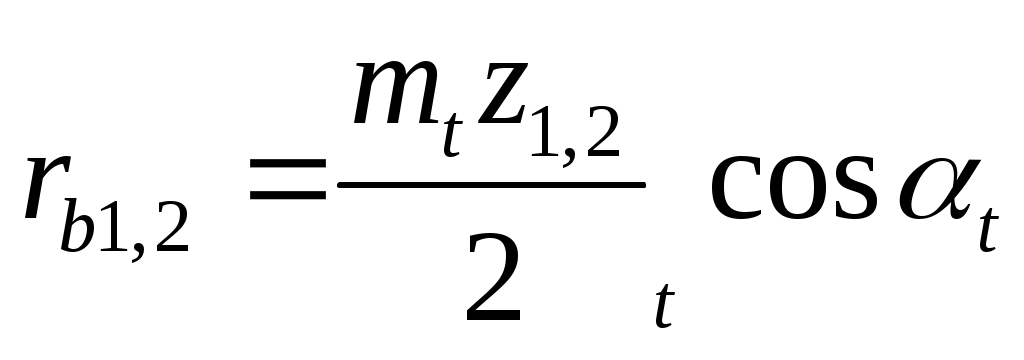 . Как уже было отмечено, требуется выполнение условия  .Определено наименьшее на колесе число зубьев без смещения, свободных от подрезания  ,а затем коэффициенты наименьшего смещения исходного контура. 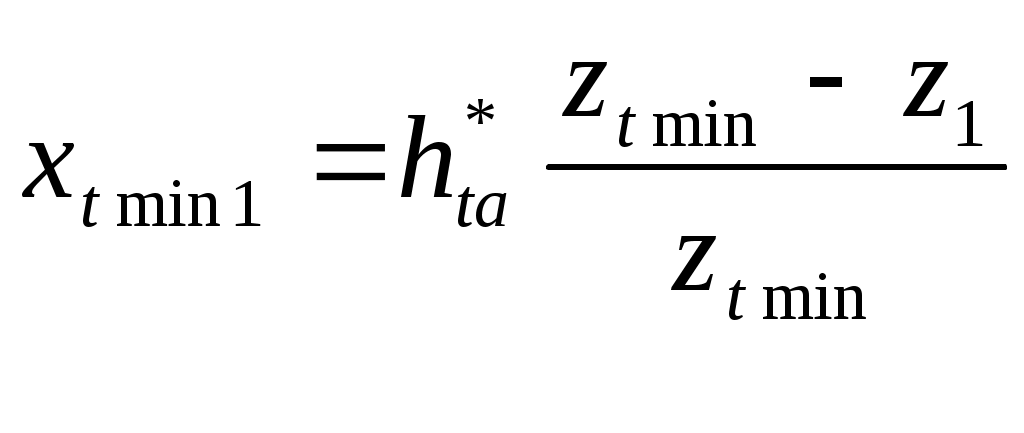 .Угол зацепления передачи определяют по формуле 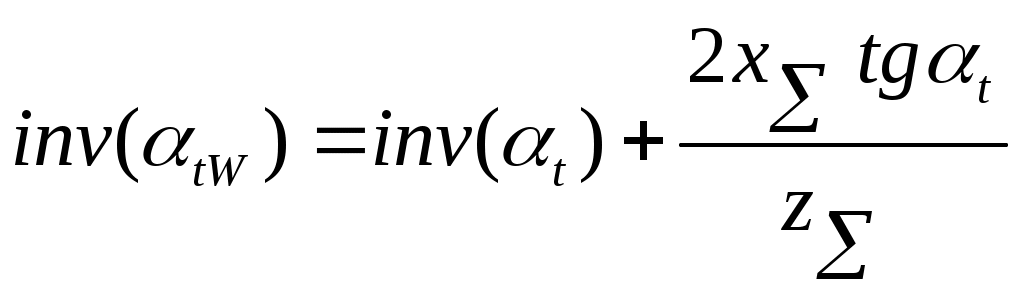 , где х=х1+х2, а z=z1+z2.При ручном счете значений угла tW находят по inv tW в таблице эвольвентных функций. Коэффициент воспринимаемого смещения  ,Коэффициент уравнительного смещения y= х-y. Радиусы начальных окружностей 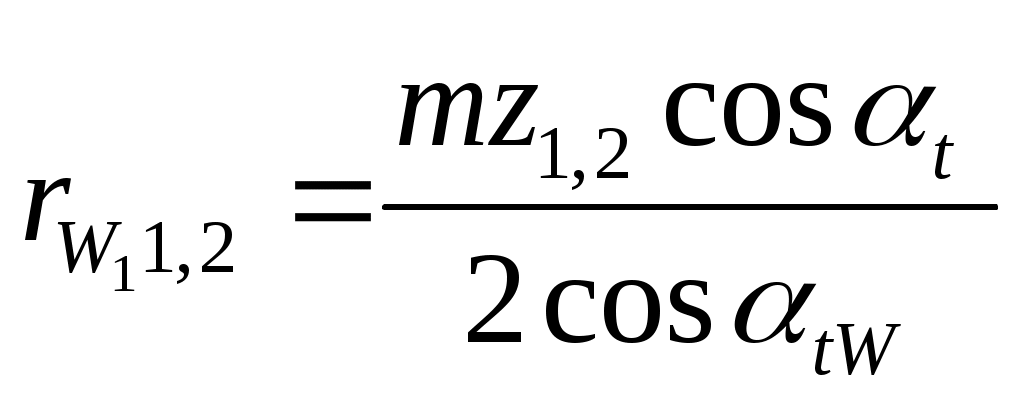 .Межосевое расстояние aW=rW1 + rW2. Радиусы окружностей вершин  .Радиусы окружностей впадин  .Высота зубьев колес  .Толщина зубьев по дугам делительных окружностей  Углы профиля на окружностях вершин зубьев колес  .Толщины зубьев по дугам окружностей вершин  .Для построения станочного зацепления дополнительно определены следующие размеры: толщина зуба s0 исходного производящего контура по делительной прямой, равная ширине впадины  ,шаг  ,радиус скругления основания ножки зуба  ,шаг по хорде делительной окружности шестерни 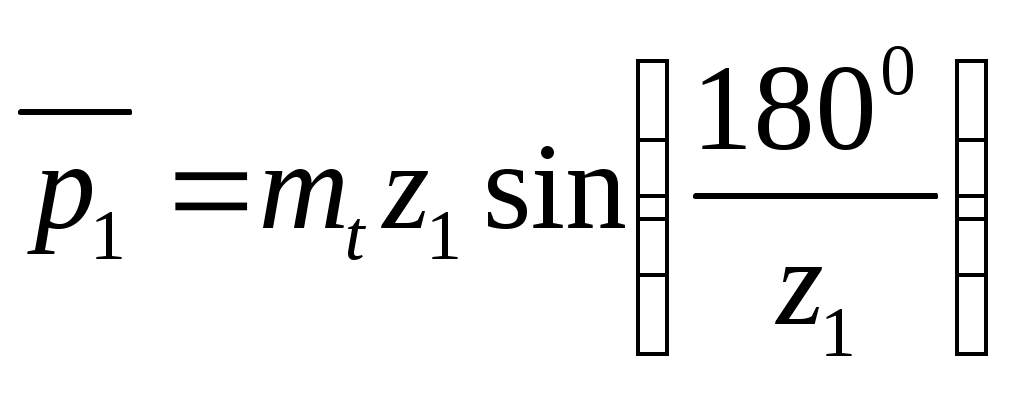 Все вышеперечисленные данные приведены в приложении 1. 3.1.2 Выбор смещения шестерни. Качественные показатели зубчатой передачи рассчитаны с помощью программы ZUB. Исходные данные для расчета: Число зубьев колес z6=8, z7=22 Модуль колес m=5 [мм]. Угол наклона линии зубьев =0 [град]. (по ГОСТ 13755-81) Угол профиля = 200, Коэффициент высоты головки и ножки зуба h*a = 1, Коэффициент радиального зазора с* = 0,25 Результаты расчета приведены в приложении 1. Качественные показатели дают возможность произвести оценку передачи при ее проектировании в отношении плавности и бесшумности зацепления, прочности и возможного износа зубьев колес в сравнении с другими передачами по тем же геометрическим показателям. Такая оценка важна для рационального выбора инструмента при проектировании передач. Для оценки качественных показателей по расчетным данным программы на листе 3 построены графики в зависимости от смещения x1 1. Коэффициента торцевого перекрытия 2. Относительной толщины зубьев по окружности вершин Sa1/m, Sa2/m 3. Коэффициентов скольжения зубьев λ1, λ2 По данным этих графиков из условий: 1. отсутствия подрезания зубьев x1 > xmin 2. отсутствия заострения зубьев Sa1/m > 0.2, Sa2/m >0.2 3. коэффициента торцевого перекрытия больше допустимого >1.05 определена область допустимых значений x1. По ГОСТ 16573-70 принимаем значение для смещения шестерни x1 = 0.6, так как оно обеспечивает необходимый коэффициент торцевого перекрытия с незначительным подрезанием зубьев. 3.1.3 Построение профиля зуба колеса. Профиль зуба изготовляемого колеса воспроизводится (образуется) как огибающая ряда положений исходного производящего контура реечного инструмента в станочном зацеплении. Схема станочного зацепления строится следующим образом: Проводим делительную d1=dw01 и основную db1 окружности, окружности вершин d1 и впадин df1. Откладываем от делительной окружности (с учетом знака) выбранное в результате анализа смещение x1mt и проводим делительную прямую исходного производящего контура реечного инструмента. На расстоянии  параллельно делительной прямой проводим прямые граничных точек, а на расстоянии  - прямые вершин и впадин зубчатой рейки; станочно-начальную прямую проводим касательно к делительной окружности в точке P0 (полюс станочного зацепления).Проводим линию станочного зацепления N1P0 через полюс станочного зацепления P0 касательно к основной окружности в точке N1. Эта линия образует с прямыми исходного производящего контура инструмента углы, равные . От точки пересечения оси зубчатого колеса с делительной прямой откладываем по делительной прямой отрезки равные 1/4 шага и через их концы перпендикулярно к линии зацепления  проводим наклонную прямую, которая образует угол  с осью симметрии. Эта прямая является прямолинейной частью профиля зуба исходного производящего контура инструмента. Закругленный участок профиля строим как сопряжение прямолинейной части контура с прямой вершин или с прямой впадин окружностью радиуса  .Построив два зуба рейки, отмечаем на делительной окружности от полюса зацепления против часовой стрелки, через равные интервалы 40 точки 1, 2, 3 … , на станочно-начальной прямой отмечаем точки 1’, 2’, 3’, … , через интервалы равные длине дуги между соседними точками на делительной окружности. Объединяем зубья рейки, станочно-начальную прямую (с отмеченными на ней точками) в блок. Последовательно поворачивая зубчатую рейку на угол 40 и, совмещая соответственные точки делительной окружности и станочно-начальной прямой, обводим профиль зубчатой рейки. К полученному ряду положений профиля зуба исходного контура проводим огибающую, которая определяет левый профиль зуба изготовляемого колеса. Отразив относительно оси зубчатого колеса часть полученного профиля, получим полный профиль зуба шестерни. 3.1.4 Построение проектируемой зубчатой передачи. Проектируемую зубчатую передачу строим по ранее вычисленным с помощью ЭВМ параметрам : Откладываем межосевое расстояние  и проводим окружности: начальные rw1, rw2; делительные r1, r2 и основные rb1, rb2; окружности вершин ra1, ra2 и впадин rf1, rf2. Начальные окружности должны касаться в полюсе зацепления. Расстояние между делительными окружностями по осевой линии равно воспринимаемому смещению  . Расстояние между окружностями вершин одного колеса и впадин другого, измеренное по осевой линии, должно быть равно радиальному зазору  .Через полюс зацепления касательно к основным окружностям колес проводим линию зацепления. Точки касания  и  называются предельными точками линии зацепления. Линия зацепления образует с перпендикуляром, восстановленным к осевой линии в полюсе, угол зацепления. Буквами  и  отмечена активная линия зацепления.Профили зубьев шестерни переносятся на чертеж проектируемой передачи со схемы станочного зацепления с помощью шаблона; эвольвентную часть профиля зуба колеса строим, как траекторию точки прямой при перекатывании ее по основной окружности колеса без скольжения и переносим в точку контакта зубьев  на линию зацепления. Переходную часть профиля зуба строим приближенно. От построенного профиля зуба откладываем толщину зуба по делительной окружности и проводим аналогичный профиль другой стороны зуба.3.2 Проектирование планетарного редуктора Исходные данные: 1. Число сателлитов в редукторе к=3, 2  . Модуль зубчатых колес m=5; 3. Передаточное отношение редуктора Задан планетарный однорядный механизм. Входное звено – звено 8; Выходное – водило. 3.2.1Подбор чисел зубьев Если бы ось в планетарном механизме стала неподвижной, то мы могли бы записать:  (1)Обратим мысленно планетарный механизм в механизм с неподвижным водилом, для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения). В обращенном движении каждое из звеньев будет иметь: 8 звено: ω*8 = ω8 + (–ωн) 7 звено: ω*7 = ω7 + (–ωн)= –ωн 6 звено: ω*6 = ω6 + (–ωн) ω*н = ωн + (–ωн) = 0 , тогда из уравнения (1) получим  если (1) переписать через количество зубьев, то  (здесь минус, так как зацепление внешнее), тогда уравнение передаточного отношения будет - плюсовой механизм (2)Подставим в уравнение (2) значения передаточного числа для заданного механизма:  Зададимся числом зубьев z8 так, чтобы отсутствовал подрез у зубчатых колес и числа зубьев были целыми , т.е. z8 18 и z7 85, тогда z8 = 45, z7 = 2 . 45 = 90 ≥ 85. Заклинивания нет, z7 – z8 =90-45=45≥8. Из условия соосности, которым определяется соосное расположение центральных колес планетарного механизма с водилом h, следует равенство межосевых расстояний зацепляющих колес: r8 + r6 = r7 – r6  z8 + z6 = z7 – z6  Проверим выполнение условий соседства и сборки: Уравнение условия соседства имеет вид: 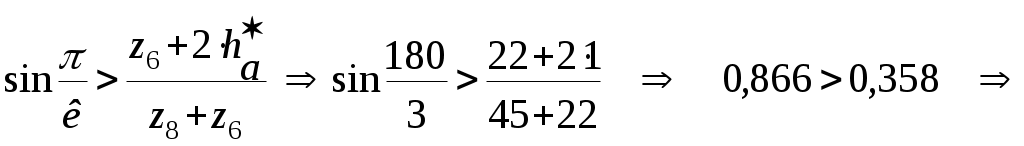 условие соседства выполнено. Уравнение условия сборки имеет вид: 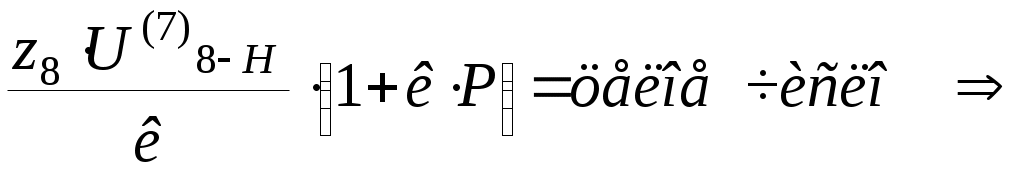 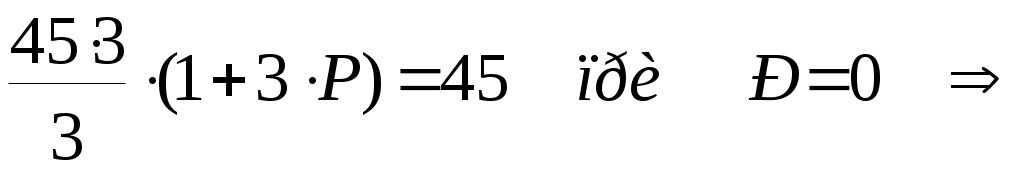 условие сборки выполнено. 3.2.2 Проверка передаточного отношения планетарного зубчатого механизма графическим способом: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||