Главная страница
Навигация по странице:

  • Проводим редукцию матрицы по строкам

  • Методом проб и ошибок

  • Методом проб и ошибок определяем матрицу назначения Х

    		•

    МОР. Задания. На базах Б1, Б2, бз имеется продукция, которую нужно доставить потребителям П1, П2, пз, П4


    Скачать 171.31 Kb.
    НазваниеНа базах Б1, Б2, бз имеется продукция, которую нужно доставить потребителям П1, П2, пз, П4
    Дата27.03.2022
    Размер171.31 Kb.
    Формат файлаdocx
    Имя файлаЗадания.docx
    ТипЗадача
    #420792
    страница2 из 2
    1   2

    Задача 2.


    Задана матрица временных затрат каждого претендента на выполнение каждой из работ


    Номера претендентов
    Номера работ

    1
    2
    3
    4
    5
    6

    1
    15
    19
    11
    4
    3
    13

    2
    14
    6
    5
    7
    8
    9

    3
    16
    7
    19
    13
    3
    7

    4
    7
    10
    9
    1
    14
    16

    5
    1
    14
    18
    4
    14
    6

    6
    5
    4
    1
    13
    10
    6


    Требуется распределить работы таким образом, чтобы минимизировать временные затраты на выполнение всех работ при условии, что каждый из претендентов получит одну и только одну работу.

    Решить задачу:

    а) венгерским методом;

    б) с помощью средства МБ Ехcel Поиск решения.

    Исходная матрица имеет вид:

    15
    19
    11
    4
    3
    13

    14
    6
    5
    7
    8
    9

    16
    7
    19
    13
    3
    7

    7
    10
    9
    1
    14
    16

    1
    14
    18
    4
    14
    6

    5
    4
    1
    13
    10
    6


    Математическая модель задачи:

    F = ∑∑cijxij, (1)

    при условиях:

    ∑xij = n, i = 1,2,…, m, (2)

    ∑xij = m, j = 1,2,…, n, (3)

    xij ≥ 0, целые

    Запишем экономико-математическую модель для нашей задачи.

    Переменные xij принимают значения 1, если i-й кандидат занимает j-ю вакансию. Если данное условие не выполняется, то xij=0.

    Ограничения по кандидатам:

    x11 + x12 + x13 + x14 + x15 + x16 = 1

    x21 + x22 + x23 + x24 + x25 + x26 = 1

    x31 + x32 + x33 + x34 + x35 + x36 = 1

    x41 + x42 + x43 + x44 + x45 + x46 = 1

    x51 + x52 + x53 + x54 + x55 + x56 = 1

    x61 + x62 + x63 + x64 + x65 + x66 = 1

    Ограничения по вакансиям:

    x11 + x21 + x31 + x41 + x51 + x61 = 1

    x12 + x22 + x32 + x42 + x52 + x62 = 1

    x13 + x23 + x33 + x43 + x53 + x63 = 1

    x14 + x24 + x34 + x44 + x54 + x64 = 1

    x15 + x25 + x35 + x45 + x55 + x65 = 1

    x16 + x26 + x36 + x46 + x56 + x66 = 1

    Целевая функция:

    15x11 + 19x12 + 11x13 + 4x14 + 3x15 + 13x16 + 14x21 + 6x22 + 5x23 + 7x24 + 8x25 + 9x26 + 16x31 + 7x32 + 19x33 + 13x34 + 3x35 + 7x36 + 7x41 + 10x42 + 9x43 + 1x44 + 14x45 + 16x46 + 1x51 + 14x52 + 18x53 + 4x54 + 14x55 + 6x56 + 5x61 + 4x62 + 1x63 + 13x64 + 10x65 + 6x66 → min

    Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.

    12
    16
    8
    1
    0
    10
    3

    9
    1
    0
    2
    3
    4
    5

    13
    4
    16
    10
    0
    4
    3

    6
    9
    8
    0
    13
    15
    1

    0
    13
    17
    3
    13
    5
    1

    4
    3
    0
    12
    9
    5
    1


    Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент.


    12
    15
    8
    1
    0
    6

    9
    0
    0
    2
    3
    0

    13
    3
    16
    10
    0
    0

    6
    8
    8
    0
    13
    11

    0
    12
    17
    3
    13
    1

    4
    2
    0
    12
    9
    1

    0
    1
    0
    0
    0
    4


    После вычитания минимальных элементов получаем полностью редуцированную матрицу.

    Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.

    Фиксируем нулевое значение в клетке (1, 5). Другие нули в строке 1 и столбце 5 вычеркиваем. Для данной клетки вычеркиваем нули в клетках (3; 5)

    Фиксируем нулевое значение в клетке (2, 2). Другие нули в строке 2 и столбце 2 вычеркиваем. Для данной клетки вычеркиваем нули в клетках (2; 3), (2; 6).

    Фиксируем нулевое значение в клетке (3, 6). Другие нули в строке 3 и столбце 6 вычеркиваем.

    Фиксируем нулевое значение в клетке (4, 4). Другие нули в строке 4 и столбце 4 вычеркиваем.

    Фиксируем нулевое значение в клетке (5, 1). Другие нули в строке 5 и столбце 1 вычеркиваем.

    Фиксируем нулевое значение в клетке (6, 3). Другие нули в строке 6 и столбце 3 вычеркиваем.

    В итоге получаем следующую матрицу:

    12
    15
    8
    1
    [0]
    6

    9
    [0]
    [-0-]
    2
    3
    [-0-]

    13
    3
    16
    10
    [-0-]
    [0]

    6
    8
    8
    [0]
    13
    11

    [0]
    12
    17
    3
    13
    1

    4
    2
    [0]
    12
    9
    1


    Количество найденных нулей равно k = 6. В результате получаем эквивалентную матрицу Сэ:

    12
    15
    8
    1
    0
    6

    9
    0
    0
    2
    3
    0

    13
    3
    16
    10
    0
    0

    6
    8
    8
    0
    13
    11

    0
    12
    17
    3
    13
    1

    4
    2
    0
    12
    9
    1


    Методом проб и ошибок определяем матрицу назначения Х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить минимальную стоимость назначения.

    12
    15
    8
    1
    [0]
    6

    9
    [0]
    [-0-]
    2
    3
    [-0-]

    13
    3
    16
    10
    [-0-]
    [0]

    6
    8
    8
    [0]
    13
    11

    [0]
    12
    17
    3
    13
    1

    4
    2
    [0]
    12
    9
    1


    Cmin = 3 + 6 + 7 + 1 + 1 + 1 = 19

    Путь: (1;5), (2;2), (3;6), (4;4), (5;1), (6;3)
    Решение в Excel

    Создаем шаблон решения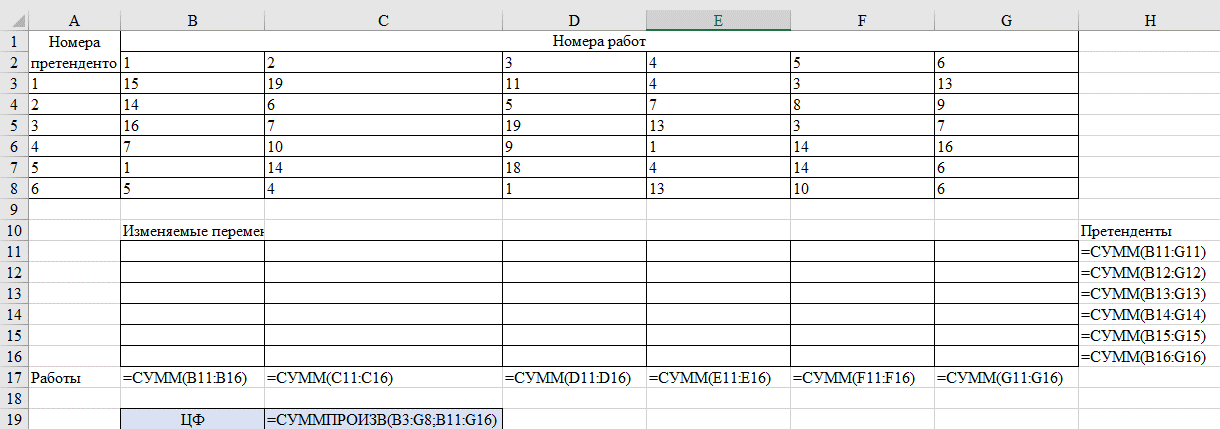



    Заполняем окно инструмента Поиск решения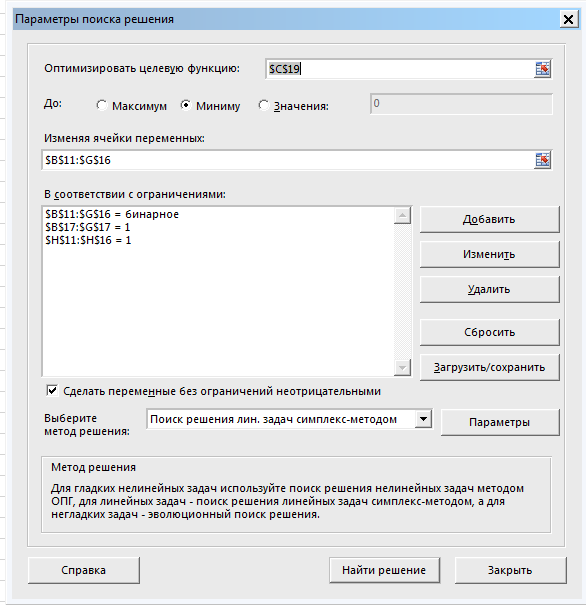


    Решение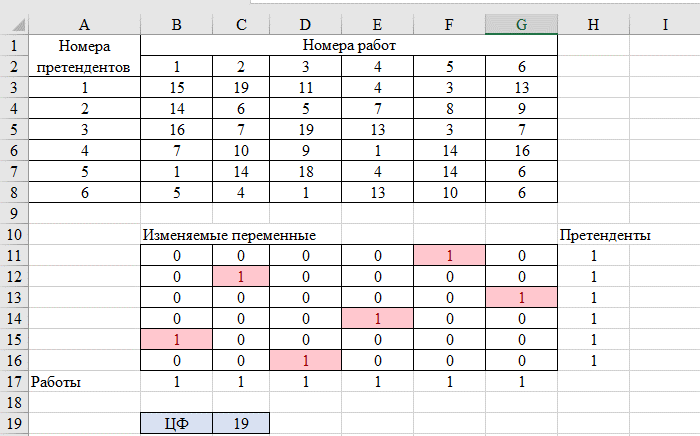


    Претендент 1 должен быть назначен на работу 5

    Претендент 2 должен быть назначен на работу 2

    Претендент 3 должен быть назначен на работу 6

    Претендент 4 должен быть назначен на работу 4

    Претендент 5 должен быть назначен на работу 1

    Претендент 6 должен быть назначен на работу 3
    Решения, полученные двумя способами, полностью совпали.

    Минимальные затраты = 19.
    1   2

    написать администратору сайта