Главная страница
Навигация по странице:

  • 5 - 5 = 0 5 - 5 = 0

  • Анализ оптимального плана

    		•

    МОР. Задания. На базах Б1, Б2, бз имеется продукция, которую нужно доставить потребителям П1, П2, пз, П4


    Скачать 171.31 Kb.
    НазваниеНа базах Б1, Б2, бз имеется продукция, которую нужно доставить потребителям П1, П2, пз, П4
    Дата27.03.2022
    Размер171.31 Kb.
    Формат файлаdocx
    Имя файлаЗадания.docx
    ТипЗадача
    #420792
    страница1 из 2
      1   2

    Задача 1.


    На базах Б1, Б2, БЗ имеется продукция, которую нужно доставить потребителям П1, П2, ПЗ, П4. Запасы продукции на базах, заказы потребителей и тарифы перевозок заданы таблицей:

     
    П1
    П2
    П3
    П4
    Запасы

    Б1
    19
    9
    6
    7
    30

    Б2
    5
    7
    10
    9
    20

    БЗ
    8
    5
    8
    6
    60

    Заказ
    30
    10
    15
    60
     


    Требуется:

    1) Составить опорные планы, используя а) метод северо-западного угла б) метод минимальной стоимости.

    2) Построить математическую модель задачи.

    3) Решить задачу с помощью средства Ехзсе! Поиск решения. Сравнить результаты, полученные в пунктах 1) и 3).
    Математическая модель транспортной задачи:

    F = ∑∑cijxij, (1)

    при условиях:

    ∑xij = ai, i = 1,2,…, m, (2)

    ∑xij = bj, j = 1,2,…, n, (3)

    xij ≥ 0

    Запишем экономико-математическую модель для нашей задачи.

    Переменные:

    x11 – количество груза из 1-го склада к 1-у потребителю.

    x12 – количество груза из 1-го склада к 2-у потребителю.

    x13 – количество груза из 1-го склада к 3-у потребителю.

    x14 – количество груза из 1-го склада к 4-у потребителю.

    x21 – количество груза из 2-го склада к 1-у потребителю.

    x22 – количество груза из 2-го склада к 2-у потребителю.

    x23 – количество груза из 2-го склада к 3-у потребителю.

    x24 – количество груза из 2-го склада к 4-у потребителю.

    x31 – количество груза из 3-го склада к 1-у потребителю.

    x32 – количество груза из 3-го склада к 2-у потребителю.

    x33 – количество груза из 3-го склада к 3-у потребителю.

    x34 – количество груза из 3-го склада к 4-у потребителю.

    Ограничения по запасам:

    x11 + x12 + x13 + x14 ≤ 30 (для 1 базы)

    x21 + x22 + x23 + x24 ≤ 20 (для 2 базы)

    x31 + x32 + x33 + x34 ≤ 60 (для 3 базы)

    Ограничения по потребностям:

    x11 + x21 + x31 = 30 (для 1-го потребителя.)

    x12 + x22 + x32 = 10 (для 2-го потребителя.)

    x13 + x23 + x33 = 15 (для 3-го потребителя.)

    x14 + x24 + x34 = 60 (для 4-го потребителя.)

    Целевая функция:

    19x11 + 9x12 + 6x13 + 7x14 + 5x21 + 7x22 + 10x23 + 9x24 + 8x31 + 5x32 + 8x33 + 6x34 → min

    Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов




    B1
    B2
    B3
    B4
    Запасы

    A1
    19
    9
    6
    7
    30

    A2
    5
    7
    10
    9
    20

    A3
    8
    5
    8
    6
    60

    Потребности
    30
    10
    15
    60




    Проверим необходимое и достаточное условие разрешимости задачи.

    ∑a = 30 + 20 + 60 = 110

    ∑b = 30 + 10 + 15 + 60 = 115

    Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу с запасом груза, равным 5 (110—115). Тарифы перевозки единицы груза из базы ко всем потребителям полагаем равны нулю.

    Занесем исходные данные в распределительную таблицу.




    B1
    B2
    B3
    B4
    Запасы

    A1
    19
    9
    6
    7
    30

    A2
    5
    7
    10
    9
    20

    A3
    8
    5
    8
    6
    60

    A4
    0
    0
    0
    0
    5

    Потребности
    30
    10
    15
    60




    Используя метод северо-западного угла, построим первый опорный план транспортной задачи.

    План начинается заполняться с верхнего левого угла.

    Искомый элемент равен c11=19. Для этого элемента запасы равны 30, потребности 30. Поскольку минимальным является 30, то вычитаем его.

    x11 = min(30,30) = 30.

    19
    x
    x
    x
    30 - 30 = 0

    5
    7
    10
    9
    20

    8
    5
    8
    6
    60

    0
    0
    0
    0
    5

    30 - 30 = 0
    10
    15
    60



    Искомый элемент равен c22=7. Для этого элемента запасы равны 20, потребности 10. Поскольку минимальным является 10, то вычитаем его.

    x22 = min(20,10) = 10.

    19
    x
    x
    x
    0

    5
    7
    10
    9
    20 - 10 = 10

    8
    x
    8
    6
    60

    0
    x
    0
    0
    5

    0
    10 - 10 = 0
    15
    60




    Искомый элемент равен c23=10. Для этого элемента запасы равны 10, потребности 15. Поскольку минимальным является 10, то вычитаем его.

    x23 = min(10,15) = 10.

    19
    x
    x
    x
    0

    5
    7
    10
    x
    10 - 10 = 0

    8
    x
    8
    6
    60

    0
    x
    0
    0
    5

    0
    0
    15 - 10 = 5
    60




    Искомый элемент равен c33=8. Для этого элемента запасы равны 60, потребности 5. Поскольку минимальным является 5, то вычитаем его.

    x33 = min(60,5) = 5.

    19
    x
    x
    x
    0

    5
    7
    10
    x
    0

    8
    x
    8
    6
    60 - 5 = 55

    0
    x
    x
    0
    5

    0
    0
    5 - 5 = 0
    60




    Искомый элемент равен c34=6. Для этого элемента запасы равны 55, потребности 60. Поскольку минимальным является 55, то вычитаем его.

    x34 = min(55,60) = 55.

    19
    x
    x
    x
    0

    5
    7
    10
    x
    0

    8
    x
    8
    6
    55 - 55 = 0

    0
    x
    x
    0
    5

    0
    0
    0
    60 - 55 = 5




    Искомый элемент равен c44=0. Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.

    x44 = min(5,5) = 5.

    19
    x
    x
    x
    0

    5
    7
    10
    x
    0

    8
    x
    8
    6
    0

    0
    x
    x
    0
    5 - 5 = 0

    0
    0
    0
    5 - 5 = 0



    Далее, согласно алгоритму, ищем элементы среди не вычеркнутых.

    19
    9
    6
    7
    30

    5
    7
    10
    9
    20

    8
    5
    8
    6
    60

    0
    0
    0
    0
    5

    30
    10
    15
    60



    Искомый элемент равен c12=9, но т.к. ограничения выполнены, то x12=0.




    B1
    B2
    B3
    B4
    Запасы

    A1
    19[30]
    9[0]
    6
    7
    30

    A2
    5
    7[10]
    10[10]
    9
    20

    A3
    8
    5
    8[5]
    6[55]
    60

    A4
    0
    0
    0
    0[5]
    5

    Потребности
    30
    10
    15
    60




    В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность потребителей удовлетворена, а план соответствует системе ограничений транспортной задачи.

    Значение целевой функции для этого опорного плана равно:

    F(x) = 19*30 + 7*10 + 10*10 + 8*5 + 6*55 + 0*5 = 1110
    Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

    Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj.

    Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.

    Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

    Искомый элемент равен c21=5. Для этого элемента запасы равны 20, потребности 30. Поскольку минимальным является 20, то вычитаем его.

    x21 = min(20,30) = 20.

    19
    9
    6
    7
    30

    5
    x
    x
    x
    20 - 20 = 0

    8
    5
    8
    6
    60

    0
    0
    0
    0
    5

    30 - 20 = 10
    10
    15
    60



    Искомый элемент равен c32=5. Для этого элемента запасы равны 60, потребности 10. Поскольку минимальным является 10, то вычитаем его.

    x32 = min(60,10) = 10.

    19
    x
    6
    7
    30

    5
    x
    x
    x
    0

    8
    5
    8
    6
    60 - 10 = 50

    0
    x
    0
    0
    5

    10
    10 - 10 = 0
    15
    60



    Искомый элемент равен c13=6. Для этого элемента запасы равны 30, потребности 15. Поскольку минимальным является 15, то вычитаем его.

    x13 = min(30,15) = 15.

    19
    x
    6
    7
    30 - 15 = 15

    5
    x
    x
    x
    0

    8
    5
    x
    6
    50

    0
    x
    x
    0
    5

    10
    0
    15 - 15 = 0
    60



    Искомый элемент равен c34=6. Для этого элемента запасы равны 50, потребности 60. Поскольку минимальным является 50, то вычитаем его.

    x34 = min(50,60) = 50.

    19
    x
    6
    7
    15

    5
    x
    x
    x
    0

    x
    5
    x
    6
    50 - 50 = 0

    0
    x
    x
    0
    5

    10
    0
    0
    60 - 50 = 10



    Искомый элемент равен c14=7. Для этого элемента запасы равны 15, потребности 10. Поскольку минимальным является 10, то вычитаем его.

    x14 = min(15,10) = 10.

    19
    x
    6
    7
    15 - 10 = 5

    5
    x
    x
    x
    0

    x
    5
    x
    6
    0

    0
    x
    x
    x
    5

    10
    0
    0
    10 - 10 = 0



    Искомый элемент равен c11=19. Для этого элемента запасы равны 5, потребности 10. Поскольку минимальным является 5, то вычитаем его.

    x11 = min(5,10) = 5.

    19
    x
    6
    7
    5 - 5 = 0

    5
    x
    x
    x
    0

    x
    5
    x
    6
    0

    0
    x
    x
    x
    5

    10 - 5 = 5
    0
    0
    0



    Искомый элемент равен c41=0. Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.

    x41 = min(5,5) = 5.

    19
    x
    6
    7
    0

    5
    x
    x
    x
    0

    x
    5
    x
    6
    0

    0
    x
    x
    x
    5 - 5 = 0

    5 - 5 = 0
    0
    0
    0






    B1
    B2
    B3
    B4
    Запасы

    A1
    19[5]
    9
    6[15]
    7[10]
    30

    A2
    5[20]
    7
    10
    9
    20

    A3
    8
    5[10]
    8
    6[50]
    60

    A4
    0[5]
    0
    0
    0
    5

    Потребности
    30
    10
    15
    60




    В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

    Значение целевой функции для этого опорного плана равно:

    F(x) = 19*5 + 6*15 + 7*10 + 5*20 + 5*10 + 6*50 + 0*5 = 705
    Решение в Excel

    Создаем шаблон решения


    Заполняем окно инструмента Поиск решения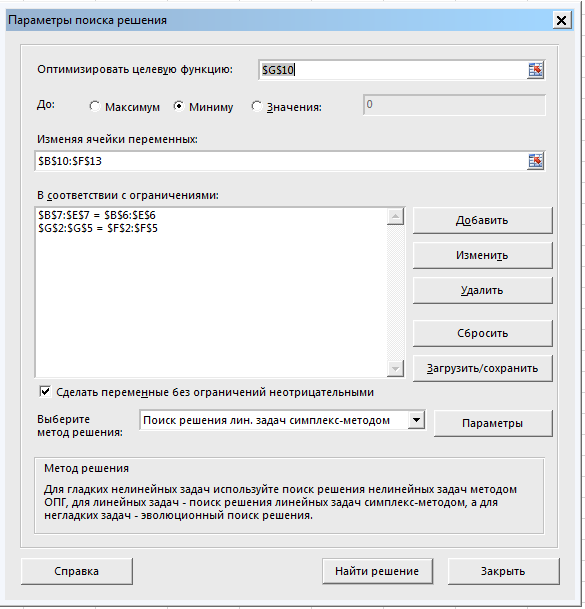


    Решение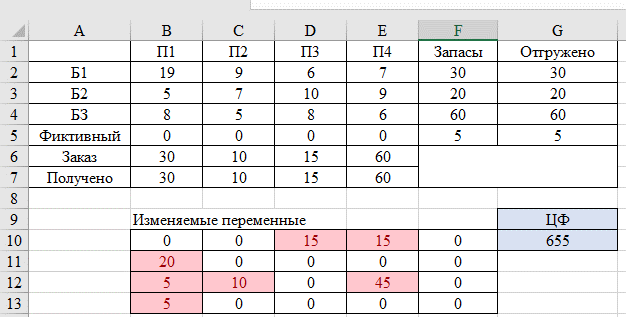



    Минимальные затраты составят: F(x) = 6*15 + 7*15 + 5*20 + 8*5 + 5*10 + 6*45 + 0*5 = 655

    Анализ оптимального плана.

    Из 1-го склада необходимо груз направить к 3-у потребителю (15 ед.), к 4-у потребителю (15 ед.)

    Из 2-го склада необходимо весь груз направить к 1-у потребителю.

    Из 3-го склада необходимо груз направить к 1-у потребителю (5 ед.), к 2-у потребителю (10 ед.), к 4-у потребителю (45 ед.)

    Потребность 1-го потребителя остается неудовлетворенной на 5 ед.
    Опорный план полученный методом северо-западного угла дает оценку ЦФ = 1110.

    Опорный план полученный методом минимальной стоимости дает оценку ЦФ = 705.

    Как видим, опорный план полученный методом минимальной стоимости, дает, для данной задачи, результат более близкий к оптимальному решению ЦФ = 655.
      1   2

    написать администратору сайта