методичка 1. На рис показана схема расположения тензометров на прямоугольном образце
 Скачать 92.6 Kb. Скачать 92.6 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 10 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ ЗУБА ШЕСТЕРНИ Цель работы. Изучение характера распределения напряжений в зоне концентрации напряжений зуба шестерни и определение величины коэффициента концентрации напряжений. Порядок проведения испытаний. Испытанию подвергается металлическая модель зуба шестерни увеличенных размеров (рис.19). Измерение напряжений проводится двумя методами: поляризационно-оптическим и тензометрическим, сущность которых описана в лабораторных работах №8 и №9. Общую картину распределения напряжений наблюдают с помощью оптически чувствительного покрытия из эпоксидной смолы, нанесенного на боковую поверхность зуба. Рис.19 Рассматривая картину изохром в поляризованном свете с помощью V-образного полярископа, определяют зону концентрации полос и наивысший порядок полосы 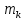 в ней. Зная порядок полосы в ней. Зная порядок полосы 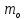 вне зоны концентрации, находят коэффициент концентрации напряжений вне зоны концентрации, находят коэффициент концентрации напряжений 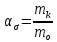 . . Полученное значение будет приближенным; более точно оно определяется тензометрическим методом. Для этого по поверхности зуба сверху наклеивают цепочкой шесть малобазных датчиков сопротивления. Модель шестерни помещают на траверсу гидравлической машины и подвергают ступенчатому сжатию силой F по кромке головки зуба. После каждой ступени нагрузки записывают в журнал наблюдений показания всех тензометров. По окончании испытаний рассчитывают средние приращения нагрузки 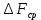  и показаний тензометров и показаний тензометров 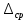 . По наибольшему значению . По наибольшему значению 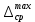 находят максимальное напряжение находят максимальное напряжение 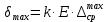 , где k- цена деления прибора. , где k- цена деления прибора.Номинальное напряжение в расчетном сечении зуба 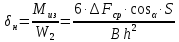 , где , где 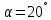 - так называемый .угол зацепления. Затем определяют опытный коэффициент концентрации - так называемый .угол зацепления. Затем определяют опытный коэффициент концентрации 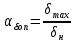 и сравнивают его с расчетным коэффициентом концентрации напряжений. Последний вычисляют по формуле: и сравнивают его с расчетным коэффициентом концентрации напряжений. Последний вычисляют по формуле: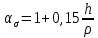 , где , где 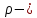 радиус закругления у ножки зуба. радиус закругления у ножки зуба.Выводы. Сравнить два метода ряжений. Отметить положение зоны концентрации напряжений , величину коэффициента концентрации и соответствие расчетному значению. ЛАБОРАТОРНАЯ РАБОТА № 11 ИЗУЧЕНИЕ ДЕФОРМАЦИИ КРУЧЕНИЯ ОБРАЗЦОВ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ. ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА Цель работы. Проверка закона Гука при кручении стального образца и определение модуля упругости для стали. Изучение процесса разрушения образцов из различных материалов и определение механических характеристик. Основные понятия и постановка испытаний. Закон Гука для кручения выражается зависимостью между деформацией и нагрузкой: 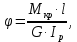 где где 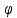 - угол закручивания; - угол закручивания; 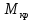 - крутящий момент. Размеры круглого образца характеризуются длинойl и полярным моментом инерции - крутящий момент. Размеры круглого образца характеризуются длинойl и полярным моментом инерции 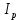 . При известных значениях l и . При известных значениях l и 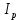 можно, измерив крутящий момент и соответствующий ему угол закручивания, подсчитать значение модуля сдвига G. можно, измерив крутящий момент и соответствующий ему угол закручивания, подсчитать значение модуля сдвига G.Для проверки справедливости закона Гука следует давать приращение нагрузки равными ступенями ( 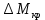 ) и замерять соответствующие приращения деформации ( ) и замерять соответствующие приращения деформации (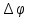 ). Построив диаграмму скручивания ). Построив диаграмму скручивания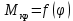 можно убедиться в наличии прямой пропорциональной зависимости до определенного значения крутящего момента можно убедиться в наличии прямой пропорциональной зависимости до определенного значения крутящего момента 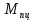 , который называют моментом пропорциональности. Далее диаграмма искривляется и медленно растет до разрушающего момента. , который называют моментом пропорциональности. Далее диаграмма искривляется и медленно растет до разрушающего момента.Для испытаний берется стальной образец диаметром d и длиной l , испытание проводится на машине К-6, развивающей максимальный момент 60 Н  м. м.Машина состоит из чугунной станины, нагружающего механизма и записывающего (диаграммного) аппарата. Кинематическая схема машины приведена на рис.20. Рис.20 Образец I установлен в зажимах машины 2 с помощью клиновых сухарей. Правый зажим поворачивают рукояткой 3 или с помощью червячной передачи 4. Угол поворота этого зажима отсчитывают по кольцу А с делениями (окружность кольца разделена на 100 частей). При повороте правого зажима образец, поворачиваясь, увлекает за собой левый зажим, поворачивая диск В на угол несколько меньший, чем кольцо А (в связи с закручиванием образца). Вместе с ним поворачивается маятник 5 и через реечную передачу 6-7 вращает диск С с делениями, поворот которого получается увеличенным в 25 раз по отношению к диску В. Левый зажим и маятник установлены на тележке, перемещаемой в зависимости от длины образца. Угол закручивания образца определяется по показаниям машины: 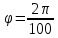 (А – В) рад., где А и В - число делений, соответственно по кольцу А и диску В. Крутящий момент зависит от перемещений (А – В) рад., где А и В - число делений, соответственно по кольцу А и диску В. Крутящий момент зависит от перемещений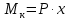 , ,Где 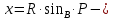 вес маятника. Вследствие малости угла поворота диска В вес маятника. Вследствие малости угла поворота диска В 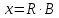 , PR= , PR=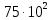 Н Н мм – постоянная машины , в связи с чем , мм – постоянная машины , в связи с чем , 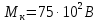 или или 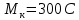 Н Н мм. мм.Нагружение образца производят путем поворота переднего зажима с помощью червячной передачи на заданное число делений по кольцу А. Число делений увеличивают каждый раз на единицу (0, 1, 2, 3...) до нарушения пропорциональности между углом и моментом. Отсчеты по шкалам А и С записывают в журнал наблюдений. Далее с помощью рукоятки доводят образец до разрушения, наблюдая характер деформации. Обработку результатов испытаний начинают с подсчета показаний по шкале В= 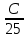 , затем определяют угол закручивания , затем определяют угол закручивания 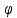 и приращение угла закручивания и приращение угла закручивания 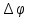 . Определяют крутящий момент . Определяют крутящий момент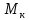 и приращение крутящего момента и приращение крутящего момента 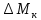 . Затем находят средние приращения угла закручивания . Затем находят средние приращения угла закручивания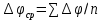 и крутящего момента и крутящего момента 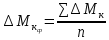 . В число наблюдений n включают только значения . В число наблюдений n включают только значения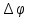 и и 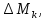 лежащие в пределах пропорциональности. Модуль сдвига лежащие в пределах пропорциональности. Модуль сдвигаиз опыта определяют по Формуле: 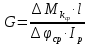 , где , где 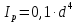 . Полученную величин сравниваем с найденной из теоретического соотношения . Полученную величин сравниваем с найденной из теоретического соотношения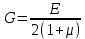 , где E и , где E и  берутся из справочника или по данным работы №1. берутся из справочника или по данным работы №1.Характеристики прочности при кручении находят по формулам: предел пропорциональности 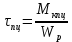 , где , где 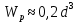 ;предел прочности ;предел прочности 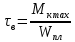 . Здесь . Здесь 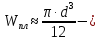 момент сопротивления сечения в пластической области - отличается от полярного момента сопротивления момент сопротивления сечения в пластической области - отличается от полярного момента сопротивления 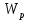 . Это вызвано отличием характера распределения напряжений в пластической области ст упругой, для которой получено выражение . Это вызвано отличием характера распределения напряжений в пластической области ст упругой, для которой получено выражение 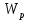 . К моменту разрушения напряжения можно считать распределенными по радиусу равномерно (рис.21, а и б). Такое распределение называют пластическим шарниром. . К моменту разрушения напряжения можно считать распределенными по радиусу равномерно (рис.21, а и б). Такое распределение называют пластическим шарниром.а) б) Рис.21 Чугунный образец испытываем на машине кручения К-50 большей мощности ( 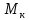 = 500 кН-м). Устройство машины в основных чертах напоминает К-6, но привод машины механический и осуществляется от электродвигателя. Образец нагружают вплоть до разрушения и замечают максимальный момент по динамометру. Предел прочности определяют по формуле = 500 кН-м). Устройство машины в основных чертах напоминает К-6, но привод машины механический и осуществляется от электродвигателя. Образец нагружают вплоть до разрушения и замечают максимальный момент по динамометру. Предел прочности определяют по формуле 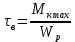 , так как у чугуна пластические деформации незначительные. В заключение необходимо зарисовать вид образцов после испытания, показав характер разрушения. Стальной образец разрушается от касательных напряжений по поперечному сечению, где. они максимальны. Чугунный - разрушается от нормальных напряжений (отрыв) по наклонному сечению под углом , так как у чугуна пластические деформации незначительные. В заключение необходимо зарисовать вид образцов после испытания, показав характер разрушения. Стальной образец разрушается от касательных напряжений по поперечному сечению, где. они максимальны. Чугунный - разрушается от нормальных напряжений (отрыв) по наклонному сечению под углом  к поперечному , где максимум нормальных напряжений. к поперечному , где максимум нормальных напряжений.Вопросы для самопроверки 1.Для чего левый зажим испытательной машины К-6 расположен на тележке? 2.Меняется ли крутящий момент в стержне по длине при испытании на кручение? 3.Какой вид имеет диаграмма скручивания круглого стального образца? 4.От действия каких напряжений разрушаются стальной и чугунный образцы при кручении? 5.Какой вид имеет и как расположена поверхность разрушения круглого стального стержня при кручении? 6.Модуль сдвига - расчетная или опытная величина? 7.Изменяется ли диаметр круглого стержня при кручении? 8.Чем обусловлено появление пластического шарнира в стальном стержне при кручении? 9.Почему стальной стержень при испытании-на кручение нагревается до значительной температуры? ЛАБОРАТОРНАЯ РАБОТА № 12 ИСПЫТАНИЕ ЦИЛИНДРИЧЕСКОЙ СПИРАЛЬНОЙ ПРУЖИНУ НА СЖАТОЕ Цель работы. Построить экспериментально характеристики пружины (зависимости деформации пружины от осевой нагрузки);проверка применимости закона Гука и основных расчетных Формул; определение коэффициента жесткости пружины. Краткие теоретические сведения. В системах виброзащиты машин и конструкции часто применяют винтовые цилиндрические пружины с малым шагом витков (угол подъема витков 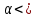 15°), подвергающиеся воздействию растягивающих или сжимающих сил. При проектировании таки?< пружин необходимо вычислять наибольшие напряжения (для оценки прочности) и деформации (для оценки жесткости). При расчете винтовых пружин обычно не учитывают деформации поперечного сдвига и изгиба витков. Расчет производят только на деформацию кручения. Деформацию (осадку) пружины от действия силы F определяют по Формуле: 15°), подвергающиеся воздействию растягивающих или сжимающих сил. При проектировании таки?< пружин необходимо вычислять наибольшие напряжения (для оценки прочности) и деформации (для оценки жесткости). При расчете винтовых пружин обычно не учитывают деформации поперечного сдвига и изгиба витков. Расчет производят только на деформацию кручения. Деформацию (осадку) пружины от действия силы F определяют по Формуле: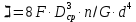 , а максимальное касательное напряжение , а максимальное касательное напряжение 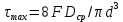 где d - диаметр проволоки, из которой изготовлена пружина; 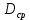 - средний диаметр пружины; n - число рабочих витков; - средний диаметр пружины; n - число рабочих витков;G - модуль сдвига материала. Отношение 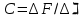 называется коэффициентом жесткости пружины. называется коэффициентом жесткости пружины.Образцы, измерительные приборы и испытательная машина . Испытаниям подвергается цилиндрическая пружина тягового динамометра системы В.П.Горячкина со следующими размерами. 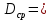 95 мм , d= 20 мм, n=4. 95 мм , d= 20 мм, n=4. Для измерения геометрических параметров применяют штангенциркуль с диапазоном 0...300 мм и слесарную металлическую линейку. Испытания проводят на машине Р-5, описанной в лабораторной работе № 1. Порядок проведения испытаний. Пружину установить на опору испытательной машины и нагрузить (рис.22) сжимающими силами. Значение нагрузки определяется по динамометру испытательном машины, а осадка - по линейке, закрепленной на подвижной опоре. По полученным данным строят график в ко ординатах F- 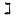 и определяют коэффициннт жесткости пружины. Полученный график называют характеристикой пружины. и определяют коэффициннт жесткости пружины. Полученный график называют характеристикой пружины.Выводы. Сопоставить значения осадки пружины, полученные из опыта и по расчетной формуле. Оценить величину 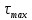 для для 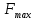 , при которой «схопываются» витки пружины и сделать заключение о прочности материала пружины. Вычислить максимальное напряжение с учетом сдвига и сделать вывод о точности приближенной Формулы. Дать заключение с применимости закона Гука. , при которой «схопываются» витки пружины и сделать заключение о прочности материала пружины. Вычислить максимальное напряжение с учетом сдвига и сделать вывод о точности приближенной Формулы. Дать заключение с применимости закона Гука.Рис.21 Вопросы для самопроверки 1.Какие основные параметры характеристики пружины и зачем их определяют? 2.Какова зависимость осадки пружины и силы, вызвавшей ее? 3.Как зависит осадка пружины от ее конструктивных размеров? 4.Как зависит осадка от упругих свойств материала? 5.Как изменится жесткость пружины, если диаметр проволоки уменьшить в два раза? 6.Согласуются ли деформации пружины на сжатие с законом Гука? 7.Какая точка сечения витка пружины самая нагруженная и почему? ЛАБОРАТОРНАЯ РАБОТА № 13 ИЗУЧЕНИЕ ЗАКОНА РАСПРЕДЕЛЕНИЯ НОРМАЛЬНЫХ НАПРЯЖНИИ ПРИ ИЗГИБЕ БАЛКИ Цель работы. Изучение закона распределения нормальных напряжений в поперечном сечении балки при изгибе. Сравнение экспериментальных величин напряжений с расчетными для оценки точности расчетных формул. Постановка испытаний. Чтобы иметь возможность разместить измерительную аппаратуру, желательно выбрать балку (например, двутавровую) достаточной высоты. Обычно рекомендуют балку № 14-18, т.е. с высотой 140...180 мм, длина балки ограничивается размерами машины и составляет 1,2...1,5 м балка устанавливается на двух шарнирных опорах и нагружается сосредоточенной силой, как правило, посередине пролета (рис.23). Исследование напряжений производят в сечении на расстоянии С от опоры, так как в среднем сечении расположить измерительную аппаратуру трудно. Для удобства наблюдений тензометры или датчики можно разместить в двух•сечениях на» расстоянии С=0,5 м от каждой опоры. Обычно по высоте балки устанавливаются 6 тензометров на разных расстояниях от нейтральной оси. Расположение тензометров показано в журнале лабораторных работ. Рис.23 При использовании механических (рычажных) тензометров база крайних тензометров (на полках) выбирается 20 мм, остальных - 100 мм, так как измеряемая ими деформация меньше и требуется большая чувствительность. Можно также использовать электрические тензометры сопротивления с проволочными или фольговыми датчиками, применение которых описано в работе № 8. Испытание производится на машине УИМ-50 гидравлического типа. Порядок проведения испытаний. В начале опыта балка нагружается предварительной нагрузкой, чтобы выбрать зазоры в системе. При этом записываются показания всех тензометров. Затем нагрузку повышают равными ступенями (обычно по 10 кН) и записывают в журнал показания тензометров на каждой ступени. По окончании испытаний разгружают балку до начальной нагрузки и проверяют отсутствие остаточных деформаций, то есть убеждаются, что испытания проводились в упругой области. Далее для каждого тензометра (датчика) вычисляют приращения (разности) показаний с учетом знака и находят средние приращения. Положительный знак приращения указывает на деформацию растяжения, отрицательный - сжатия. По средним приращениям вычисляют опытные напряжения, отнесенные к приращению нагрузки: 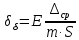 , где m и S - соответственно, масштаб и база тензометров., Параллельно находят А Л* А , где m и S - соответственно, масштаб и база тензометров., Параллельно находят А Л* Арасчетные значения напряжений 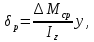 где где 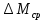 - изгибающий момент в сечении, где установлены тензометры, от нагрузки - изгибающий момент в сечении, где установлены тензометры, от нагрузки 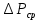 , а y - координата места установки соответствующего тензометра. Полученные величины напряжений наносят в определенном масштабе на график и строят по высоте сечения эпюры опытных и расчетных напряжений. , а y - координата места установки соответствующего тензометра. Полученные величины напряжений наносят в определенном масштабе на график и строят по высоте сечения эпюры опытных и расчетных напряжений.Выводы. Необходимо сделать вывод о характере распределения напряжений по высоте и о соответствии расчетных и опытных значений напряжений. Оценить полученные расхождения и указать причины их возникновения. Вопросы для самопроверки 1.Как по высоте сечения изменяются нормальные напряжения при изгибе балки прямоугольного сечения? 2.В каких точках сечения действуют наибольшие нормальные напряжения? 3.Почему база тензометров для измерения деформации в средней части сечения балки принимается больше, чем для тех, которые располагаются на полках двутавра? 4.Напишите формулу определения нормальных напряжений в произвольной точке. 5.Можно ли использовать для поперечного изгиба формулу нормальных напряжений, полученную для чистого изгиба? 6.В каких точках сечения действуют максимальные по абсолютной величине нормальные напряжения? ЛАБОРАТОРНАЯ РАБОТА №14 ИЗУЧЕНИЕ ДЕФОРМАЦИИ БАЛКИ ПРИ ИЗГИБЕ Цель работы. Изучение характера и величин деформаций балки. Определение опытных значений прогибов и углов поворота и сравнение их с теоретическими значениями. Постановка испытаний. Для испытаний используется балка прямоугольного сечения длиной l=1,2м, расположенная на двух опорах; нагрузка обычно прикладывается в середине пролета. Поперечное сечение балки в =50 мм, h = 10 мм располагается так, чтобы изгиб происходил в плоскости наименьшей жесткости. При этом деформации будут достаточно большими и легко доступными для измерения. Измерение прогиба производится с помощью индикатора  , установленного в среднем сечении, где прогиб имеет наибольшую величину. Наибольший угол поворота - на концах балки. Из-за трудности замера малых углов на конце балки устанавливается рычаг (рис.24), перемещение конца которого измеряется вторым индикатором , установленного в среднем сечении, где прогиб имеет наибольшую величину. Наибольший угол поворота - на концах балки. Из-за трудности замера малых углов на конце балки устанавливается рычаг (рис.24), перемещение конца которого измеряется вторым индикатором 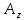 . .Порядок проведения испытаний. Перед проведением испытаний до нагружения балки устанавливают шкалы индикаторов на нуль. Затем нагружают балку равными ступенями, накладывая грузы на подвеску в середине балки (обычно Р=10 Н). При этом записывают показания индикаторов  и и  После окончания опыта нагрузку снимают и проверяют показания индикаторов, которые должны быть нулевыми. Рис.24 По показаниям индикаторов определяют опытные значения деформаций: прогиб 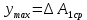 и угол поворота 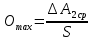 Теоретические значения, соответствующие приращению нагрузки, определяются по формулам 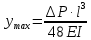 ; ; 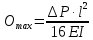 . .Можно изменять положение нагрузки по длине пролета, тогда значения деформаций рассчитывают по универсальным уравнениям или другим способом. Выводы. Необходимо сделать заключение о местах наибольших деформаций балки при изгибе, о величинах опытных и расчетных значений и их соотношении. Вопросы для самопроверки 1.Какая зависимость существует между прогибом и углом поворота в сечении балки? 2.Применим ли закон Гука для выражений деформаций балки? 3.В каких сечениях для двухопорной балки с нагрузкой посередине максимальны прогиб и угол поворота? |
