РГР по Управлению Качеством (Карты Шухарта). РГР по УК. На заводе по производству шин через каждый час контролировали
 Скачать 495.5 Kb. Скачать 495.5 Kb.
|
|
Задание 1. На заводе по производству шин через каждый час контролировали несколько шин и записывали число несоответствий. Необходимо построить контрольную карту. Объем подгрупп постоянный, n=const.
Расчет. В исходных данных не указаны объемы подгрупп (выборок), следовательно, объем подгрупп постоянный, n=const. Кроме того, анализируется число несоответствий, что, в совокупности, соответствует карте с. Среднее значение числа несоответствий в подгруппе с : с = (6 + 2 + 3 + 8 + 4 + 6 + 0 + 9 + 7 + 8 + 3 + 6 + 2 + 1 + 8)/15 = 4,86 . Ширина зоны σ σ = √с = √4,86 =2,2 . Верхняя контрольная граница UCL = c + 3σ = 4,86 + 3⋅2,2 = 11,46 . Нижняя контрольная граница LCL = 4,86 − 3⋅2,2 = − 1,74 . Принимаем LCL =0. 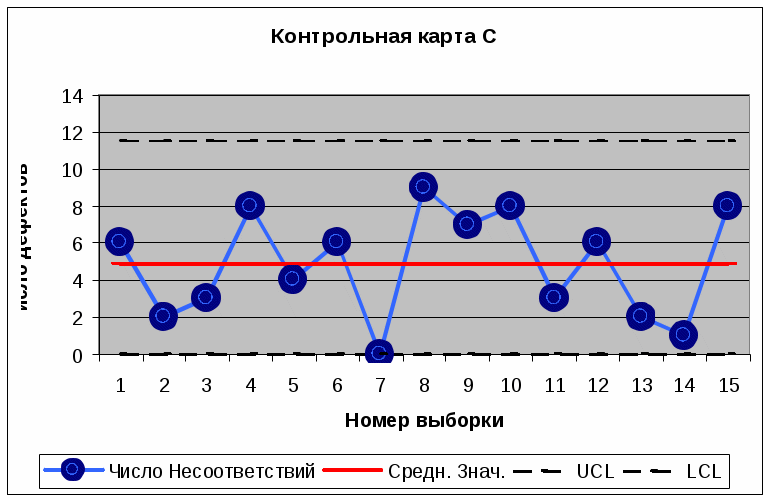 Вывод: при предварительном анализе выбросов значений за контрольные границы не обнаружено, что указывает на стабильность процесса. Задание 2. На автоматической линии производят выключатели. В каждой выборке фиксируют число несоответствующих выключателей. Объем выборки постоянный, n = 4 000 шт. Данные для построения карты np–типа
Расчет. Так как объем выборки постоянный и фиксируют несоответствующие изделия, то в данном примере применима карта np. Среднее значение np: np = (13 + 16 + 1 + 5 + 17 + 2 + 5 + 18 + 1 + 11 + 6 + 11 + 13 + 1 + 11)/15=8,73 Средний процент брака p : p = (0,325 + 0,4 + 0,025 + 0,125 + 0,05 + 0,125 + 0,45 + 0,025 + 0,275 + 0,15 + 0,15 + 0,275 + 0,325 + 0,025 + 0,275)/15= 0,19 Ширина зоны карты σ: σ = √8,73(1− 0,19) = 2,65. Верхняя контрольная граница : UCL = 8,73 + 3⋅2,65 =16,68 Нижняя контрольная граница: 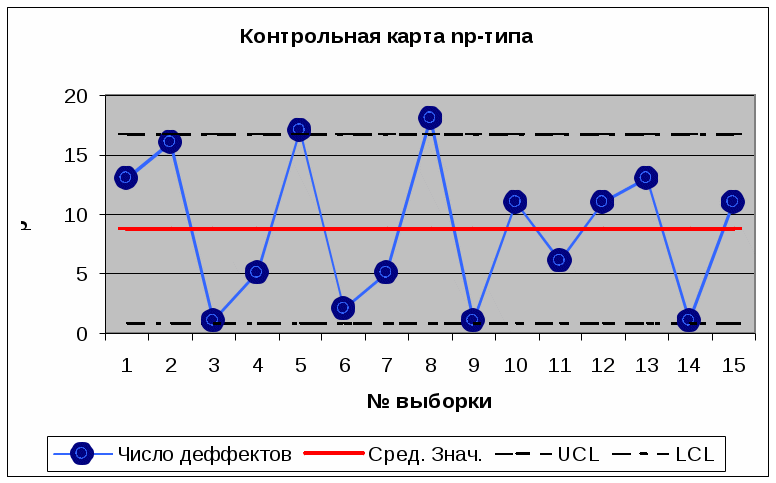 LCL = 8,73 −3⋅2,65 = 0,78 . LCL = 8,73 −3⋅2,65 = 0,78 .Вывод: в данном состоянии процесс статистически неуправляемый, т.к. число дефектных изделий в пятой и восьмой выборке вышло за верхнюю контрольную границу. Требуются корректирующие действия по улучшению процесса. Задание 3. На линии по изготовлению транзисторов в конце дня извлеклись случайные выборки (n=var) и регистрировалось количество несоответствующих изделий.
Расчет. Так как фиксируют количество несоответствующих изделий, а объемы выборок различны, то для такого случая применяют карту р. Средний объем выборки n = (115+142 +140 +140+117 +131 +141 +133+132+132+116+126+130+112+118)/15 =128,3 . Средняя доля несоответствующих изделий p = (0,11 + 0,11 + 0,007 + 0,04 + 0,145+ 0,015 + 0,035 + 0,135+0,007+0,083+0,05+0,09+0,1+0,008+0,09)/15 = 0,068. Ширина зоны карты σ = √0,068(1- 0,068)/128,3= 0,022 Верхняя контрольная граница UCL = 0,068 + 3⋅0,022 = 0,134 . Нижняя контрольная граница LCL = 0,068−3⋅0,022 = 0,002. 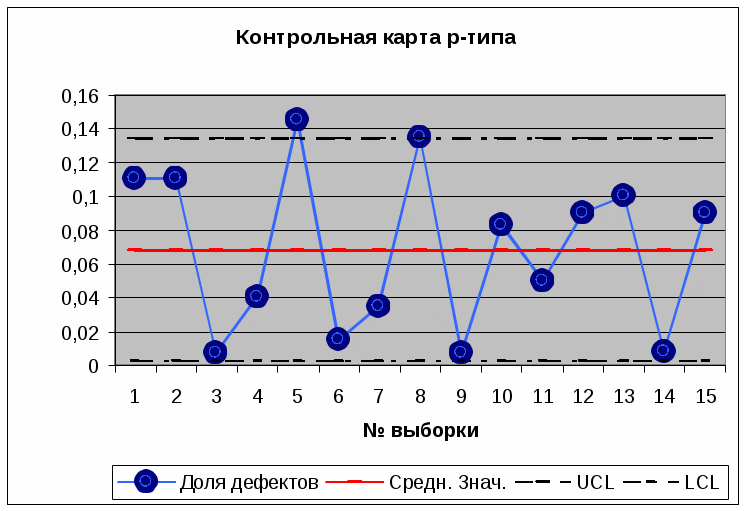 Вывод: в данном состоянии процесс статистически неуправляемый, т.к. число дефектных изделий в пятой выборке вышло за верхнюю контрольную границу. Требуются корректирующие действия по улучшению процесса. Задание 4. Деятельность некоторого подразделения предприятия заключается в подготовке ряда документов. Заказчики стали жаловаться руководителю подразделения о том, что сотрудники затягивают оформление документов. Руководитель решил провести статистическое исследование: он в течение восьми недель собирал по пять отзывов от других подразделений о длительности оформления документов его сотрудниками.
Среднее средних X^= 56,8 R^=62,6 Расчет: Для карты Х : Средняя линия контрольной карты Х соответствует значению Хˆ. Верхняя и нижняя контрольные границы определяются как UCL/LCL = X^ ± A2 ⋅ Rˆ ; где А2 – коэффициент, определяемый по табл. Средняя линия Хˆ = 56,8 мин. Объем выборки n=5; А2 = 0,577; UCL = 56,8+0,577·62,6 = 92,9 мин. LCL = 56,8 – 0,577·62,6 = 20,6 мин Для карты R: Средняя линия соответствует значению R^ . Верхняя граница контрольной карты UCL = D4 ⋅ R^ Нижняя граница контрольной карты LCL = D3 ⋅ R^ Здесь D3 и D4 определяются по табл. Средняя линия R^ = 62,6 мин. D3 = 0; D4 = 2,114. UCL = 2,114·62,6 = 132,3 мин. LCL = 0. 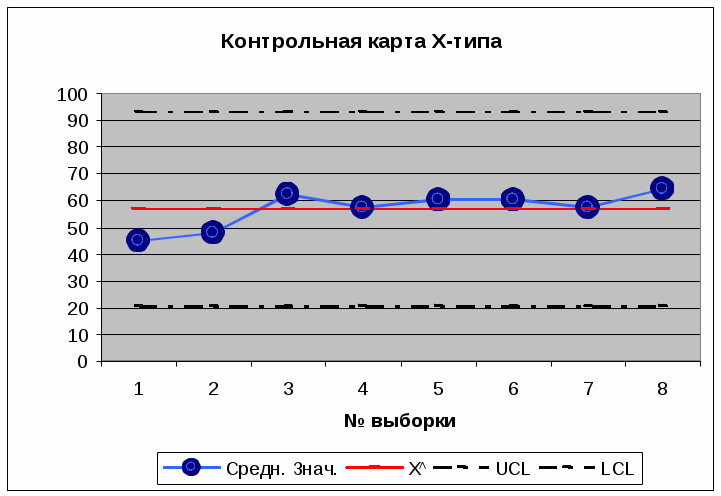 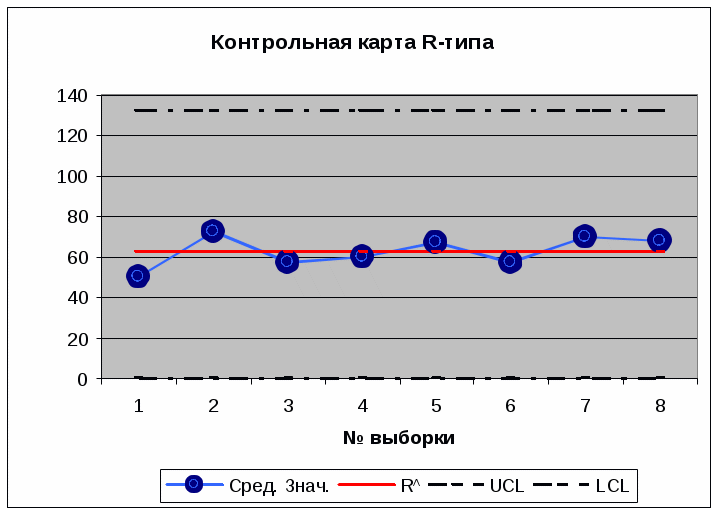 Вывод: R-карта показывает, что процесс подвержен случайным колебаниям, отсутствуют тренды, вариации среди выборок существенно не изменяются, процесс статистически управляем. Х -карта также не выходит за контрольные границы, тенденций не прослеживается, длительность обработки носит, в целом случайный характер. Определено среднестатистическое время подготовки документов, которое составило 40,6 мин, что не устраивает клиентов. Руководитель понял, что в длительности оформления виноваты не работники, а технология процесса, которую необходимо совершенствовать. Задание 5. При проведении лабораторного анализа влажности сухого молока были получены выборки из 10 последовательных партий. Выборку анализировали по таки характеристикам, как жирность, влажность, кислотность, индекс растворимости, осадки, бактерии и сывороточный протеин. Было намечено поддерживать процент влажности ниже 4%. Вариации влажности внутри одной партии оказались пренебрежительно малыми, поэтому было принято решение брать только одно наблюдение из партии Для проверки стабильности процесса изготовления сухого молока построить X - MR-карту.
Расчеты: Среднее значение влажности (значение центральной линии карты Х): Х^ =(2,9 + 3,2 + 3,6 + 4,3 + 3,8 + 3,5 + 3,1 + 3,0 + 3,6 + 3,5)/ 10= 3.45% Верхняя контрольная граница карты Х UCL = X + E2 ⋅R; UCL = 3,45+ 2,66⋅0,38 = 4,46% Нижняя контрольная граница карты Х LCL = X − E2 ⋅R; LCL = 3,45− 2,66⋅0,38 = 2,44% где Е2 = 2,66 для всех случаев. 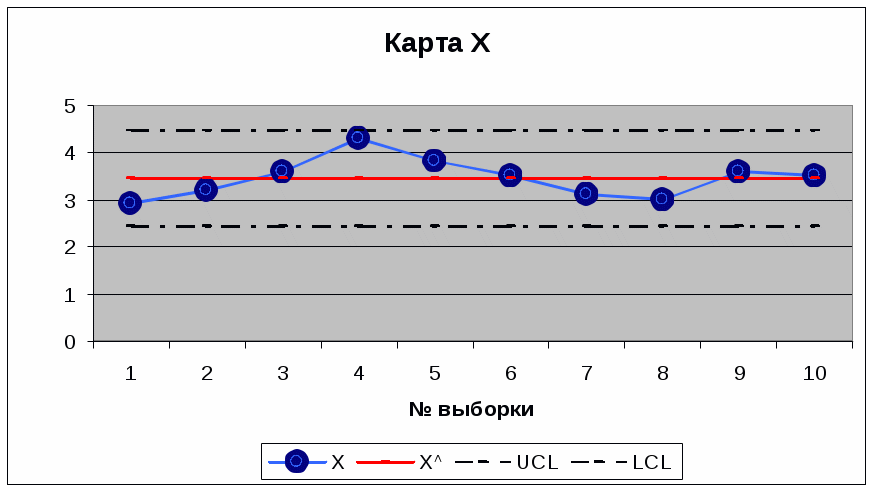 Средний размах ( значение центральной линии карты R) R^ =(0,3 + 0,4 + 0,7 + 0,5 + 0,3 + 0,4 + 0,1 + 0,6 + 0,1)/9= 0,38% Верхняя контрольная граница карты R UCL = D4 ⋅R; UCL=3,267⋅0,38= 1,24% Нижняя контрольная граница карты R LCL = D3 ⋅R; LCL= 0 г 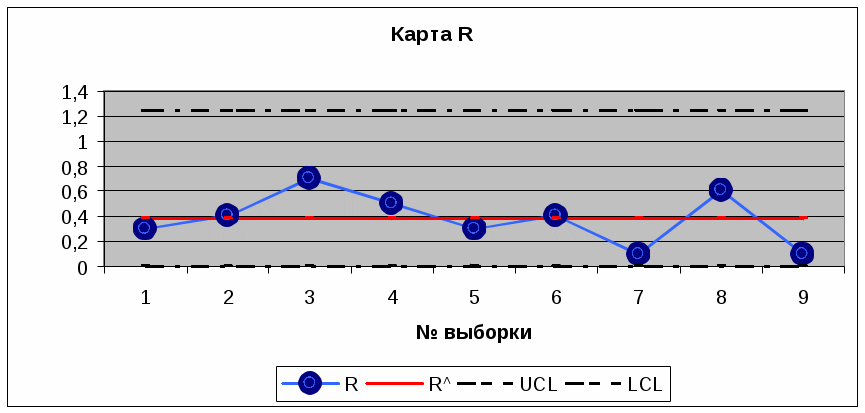 де D4 и D3 определяются по табл. де D4 и D3 определяются по табл. Вывод: Вариации влажности, о чем свидетельствует карта R, находятся в установленных границах, статистическая управляемость обеспечивается. На карте Х среднее значение влажности не превышает 4%. Выброс влажности до 4,3% представляется случайным и не вполне достоверным, так как на карте R этому соответствует выброс значения R. |
