|
|
Посібник по ЧМ. Наближення функцій
http://www.scilab.org.Exec-файл scilab-5.2.2.exe.
Наближення функцій
Наближення функцій полягає в заміні аналітично або таблично заданої функції y(x) на зручнішу для обчислень апроксимувальну функцію (x), яка б для необхідних нам значень аргументу задовольняла співвідношення 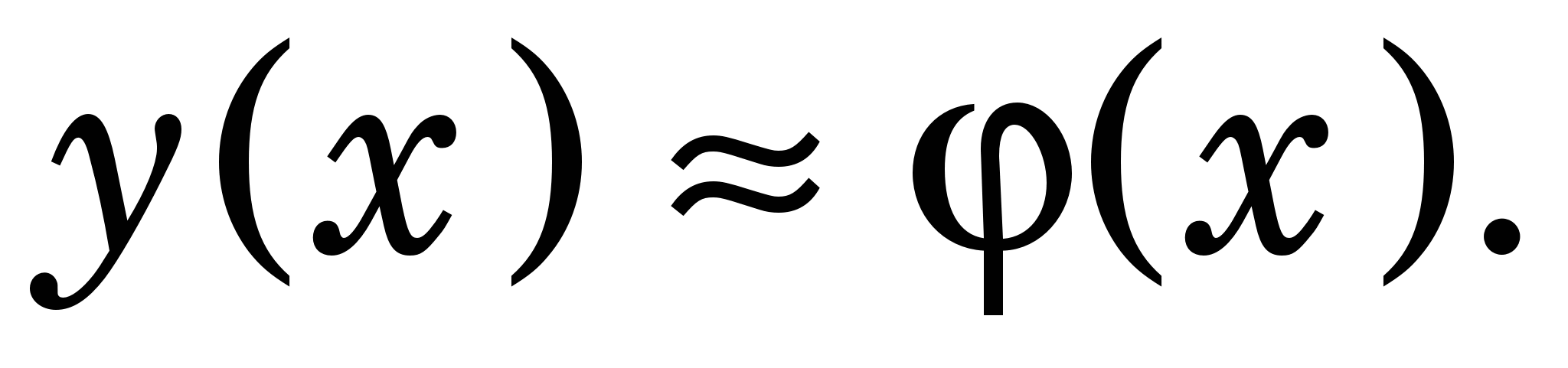 Цього досягають уведенням вектора вільних параметрів Цього досягають уведенням вектора вільних параметрів 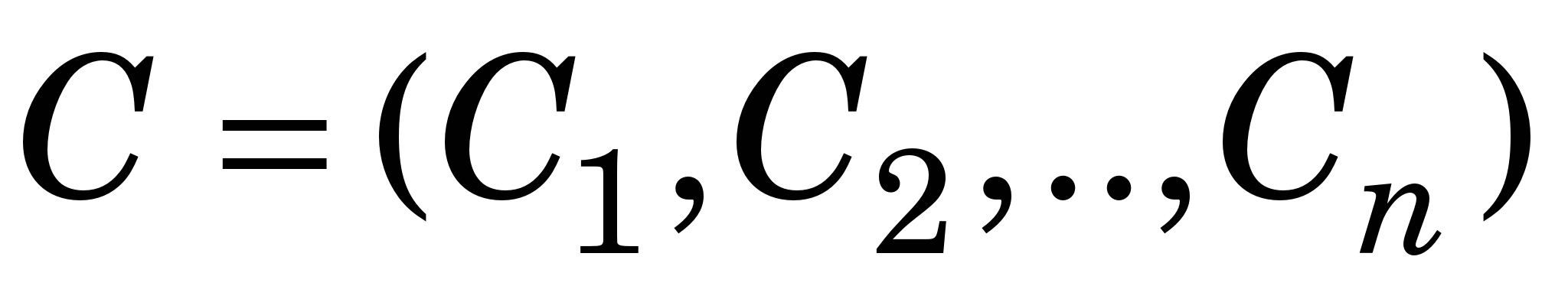 до (x) [тобто до (x) [тобто  , який визначають із умови близькості функцій y(x) та (x). Зазвичай при цьому вважають, що графіком таблично заданої функції є плавна крива. , який визначають із умови близькості функцій y(x) та (x). Зазвичай при цьому вважають, що графіком таблично заданої функції є плавна крива.
В інженерній практиці для побудови графіка функції 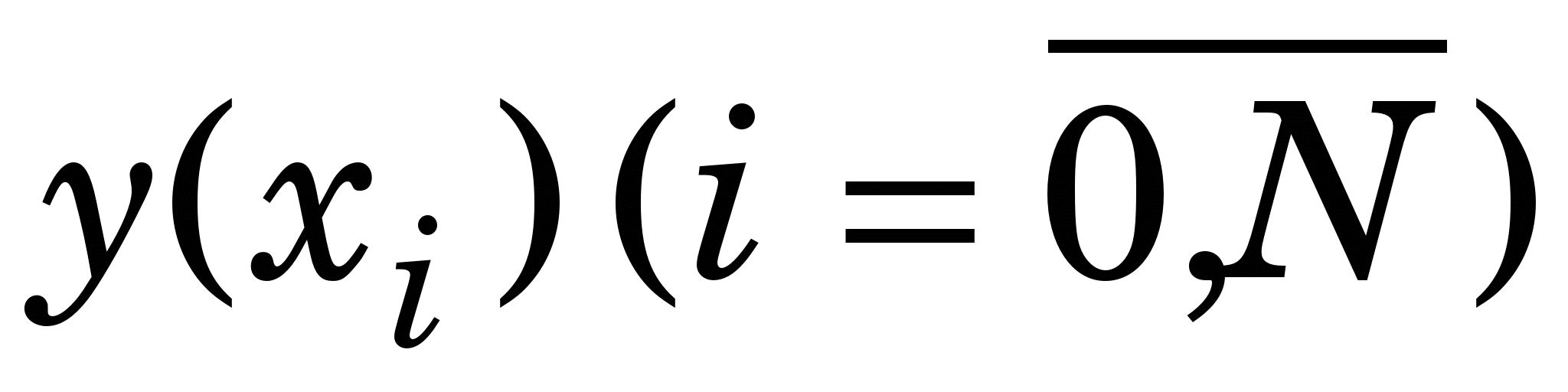 , якщо точки розташовані рідко, здебільшого беруть гнучку лінійку (spline), ставлять її на ребро і згинають так, щоб вона одночасно проходила через усі точки. Оскільки наближене рівняння згину пружного бруса має вигляд , якщо точки розташовані рідко, здебільшого беруть гнучку лінійку (spline), ставлять її на ребро і згинають так, щоб вона одночасно проходила через усі точки. Оскільки наближене рівняння згину пружного бруса має вигляд  то можна припустити, що її форма між вузлами є алгебричним поліномом 3-го степеня. Тому, очевидно, інтерполювальну функцію між кожними двома вузлами можна взяти, наприклад, у такому вигляді (кубічний сплайн): то можна припустити, що її форма між вузлами є алгебричним поліномом 3-го степеня. Тому, очевидно, інтерполювальну функцію між кожними двома вузлами можна взяти, наприклад, у такому вигляді (кубічний сплайн):
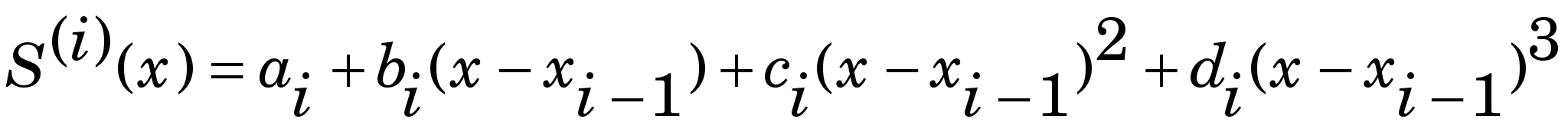 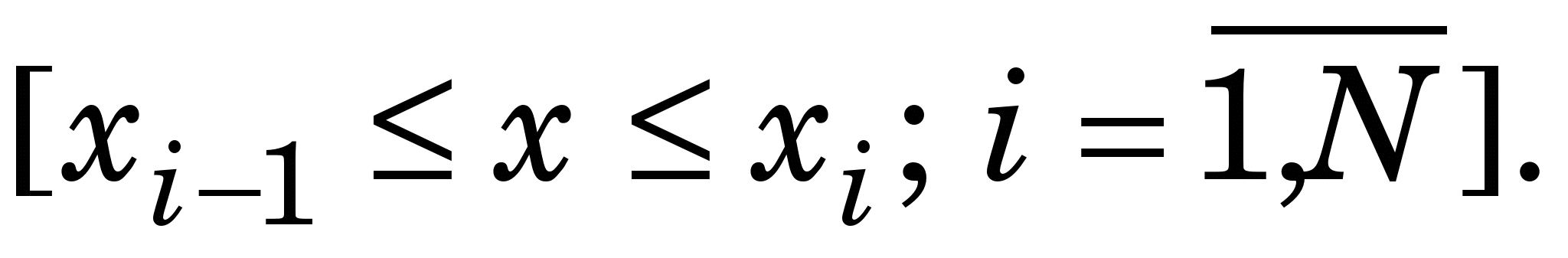
Невідомі коефіцієнти у цьому виразі 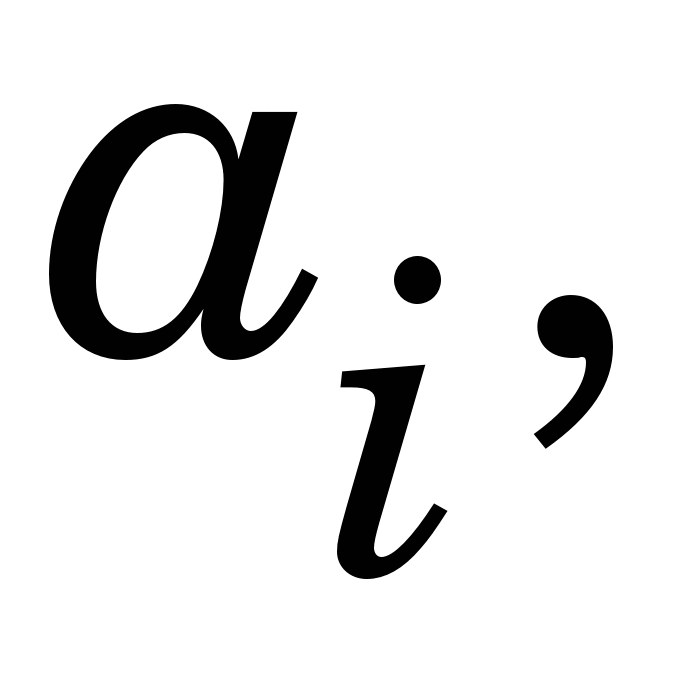 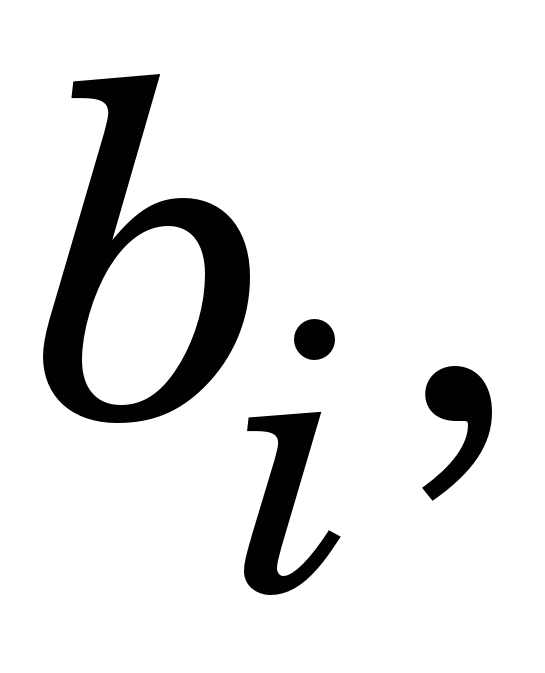 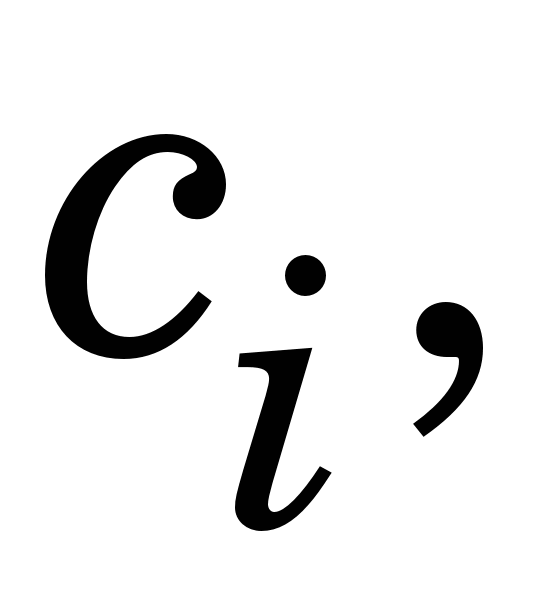 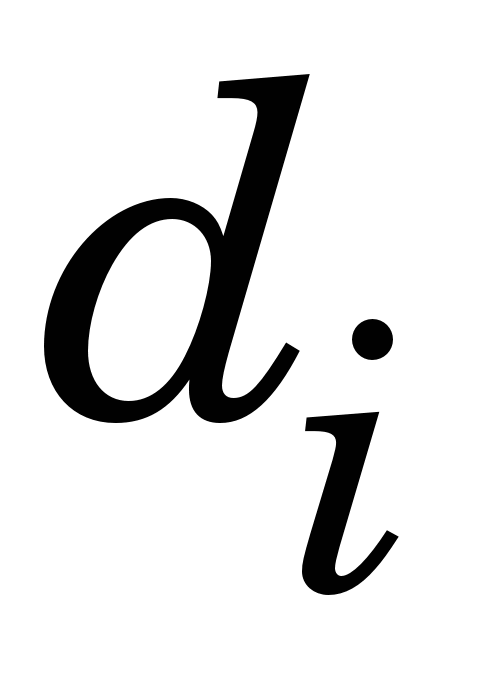 знаходять із умов у вузлах інтерполяції, зокрема знаходять із умов у вузлах інтерполяції, зокрема 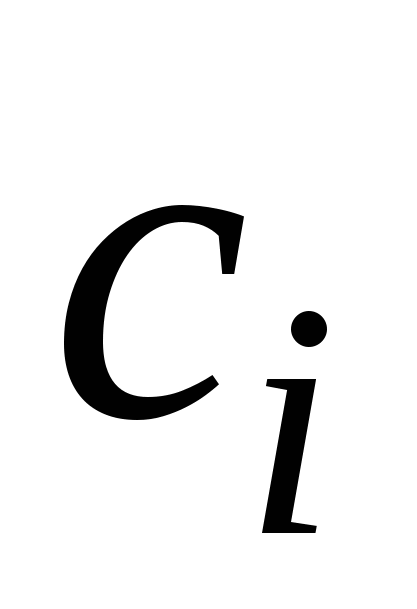 визначають із такої системи лінійних алгебричних рівнянь (СЛАР): визначають із такої системи лінійних алгебричних рівнянь (СЛАР):
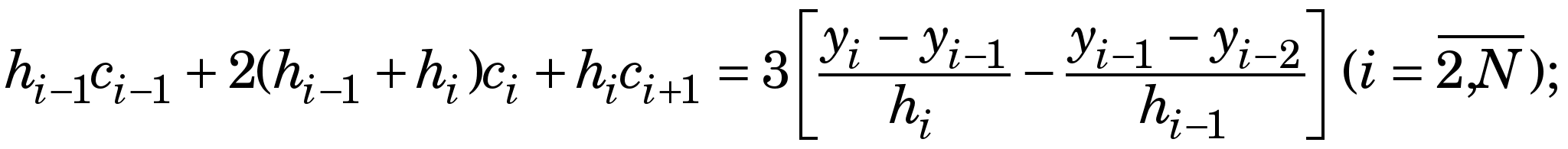
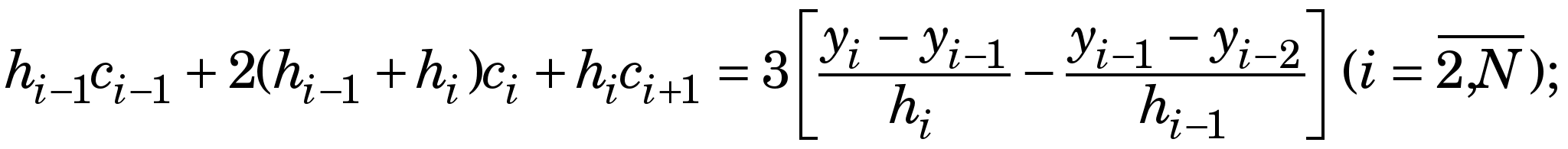  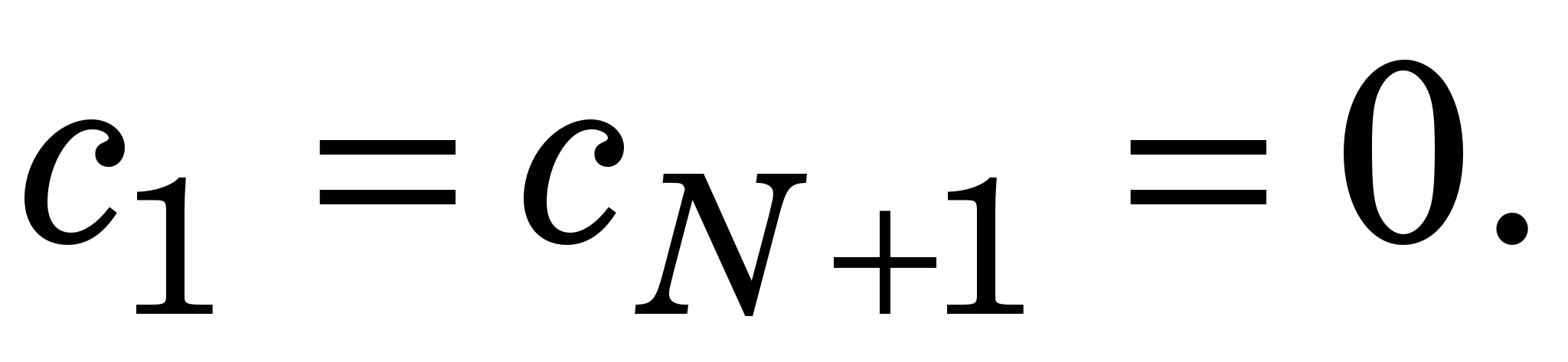 (1.1) (1.1)
Для розв’язання системи лінійних алгебричних рівнянь (1.1) (знаходження  ) варто скористатися алгебричною прогонкою, після чого ) варто скористатися алгебричною прогонкою, після чого  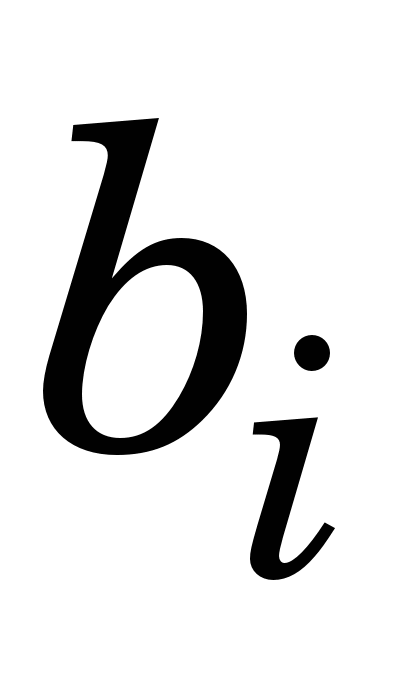 та та 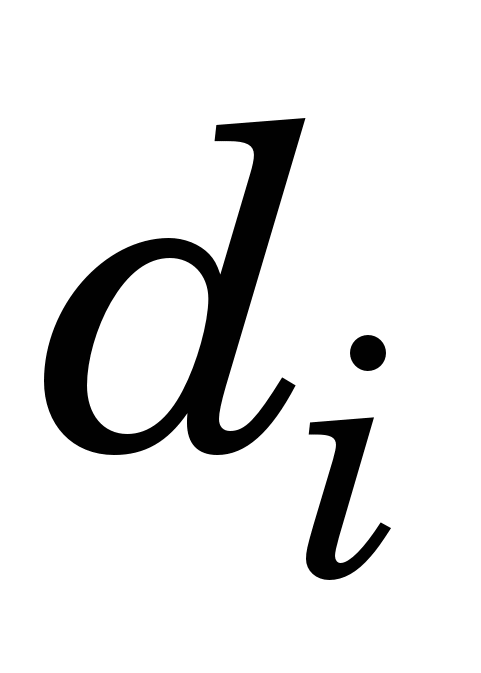 визначити такими виразами, якщо кінці лінійки вільно відпущені (вільні кубічні сплайни – ВКС): визначити такими виразами, якщо кінці лінійки вільно відпущені (вільні кубічні сплайни – ВКС):
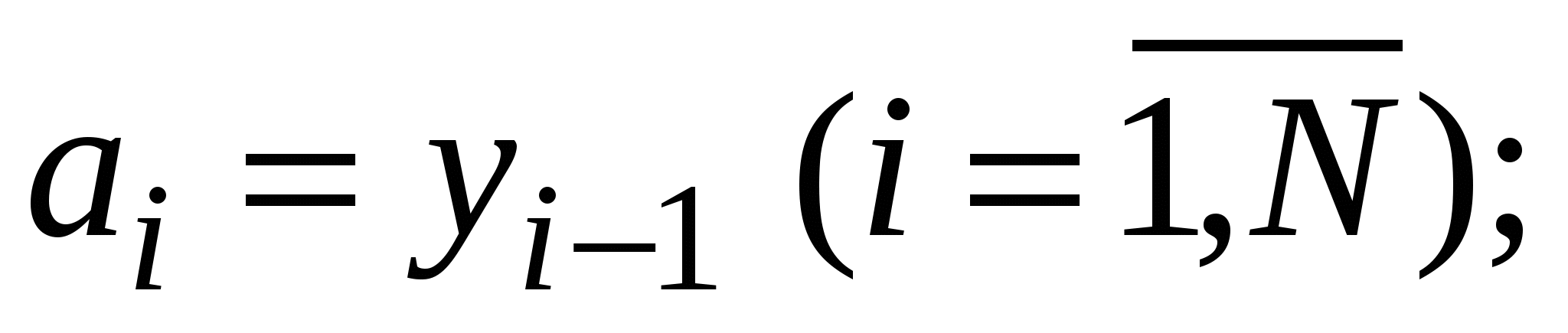 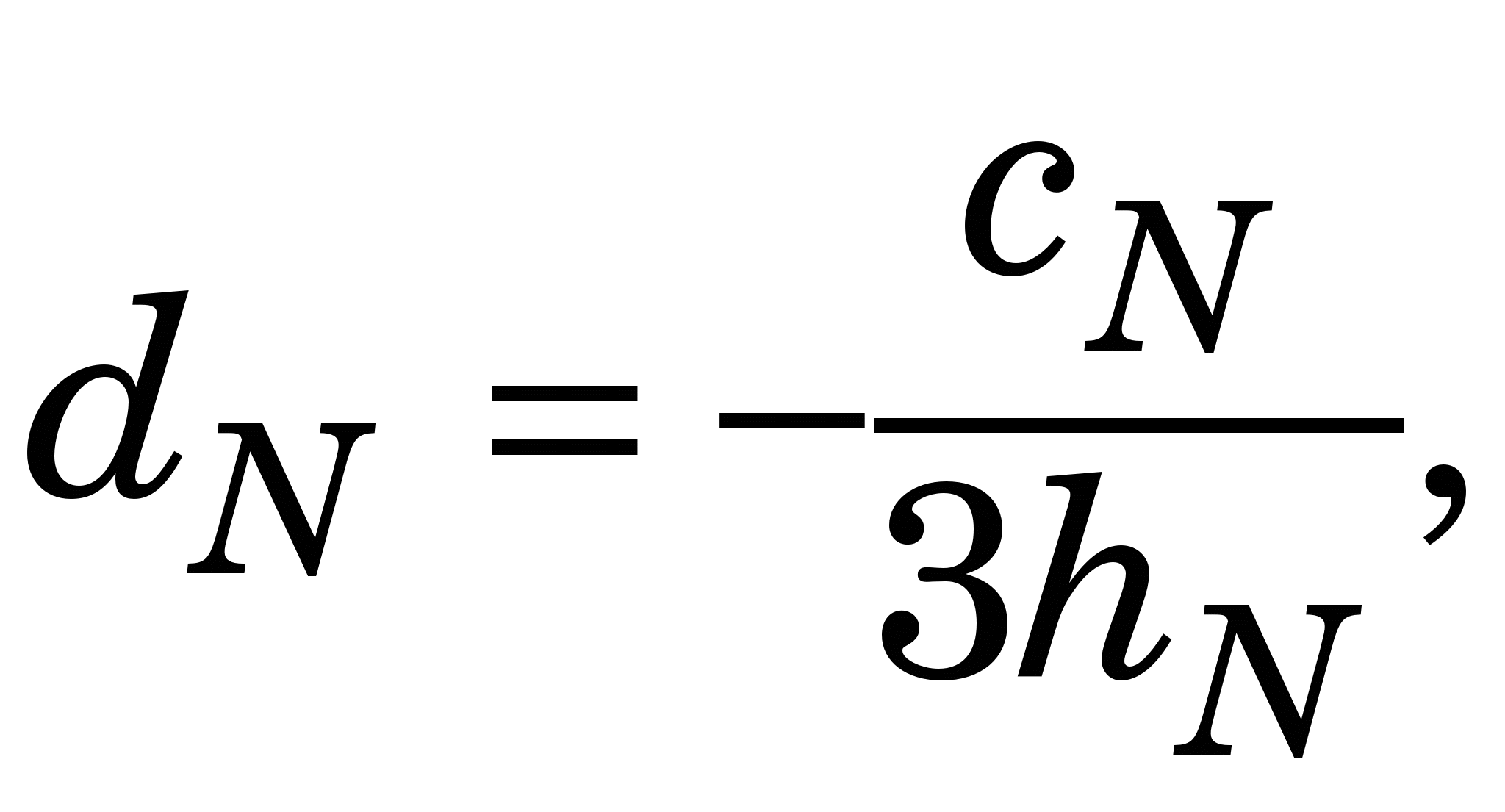 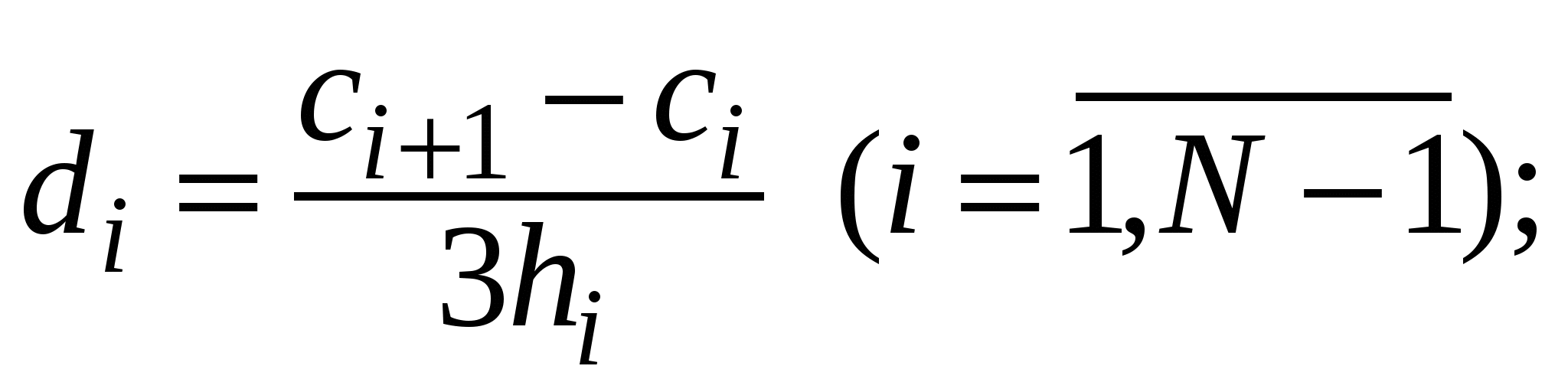
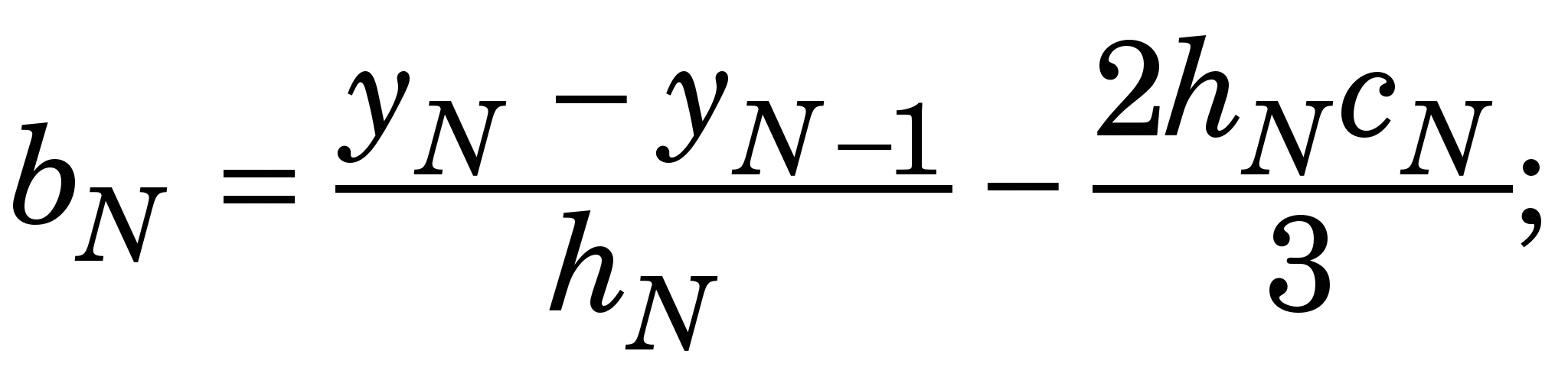 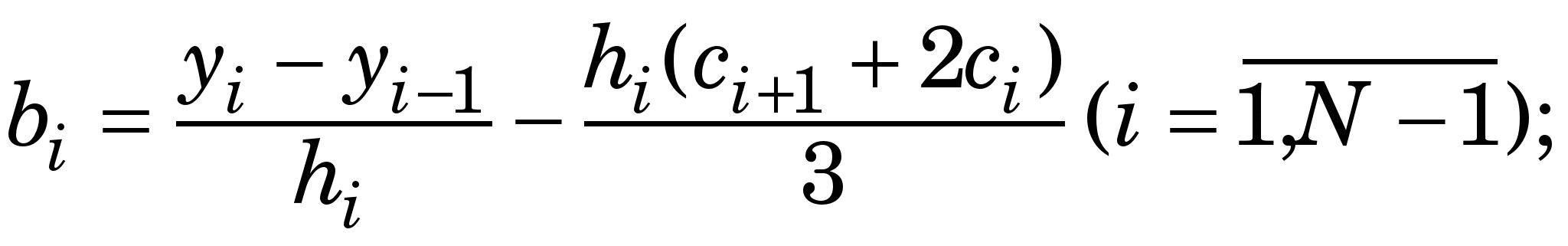 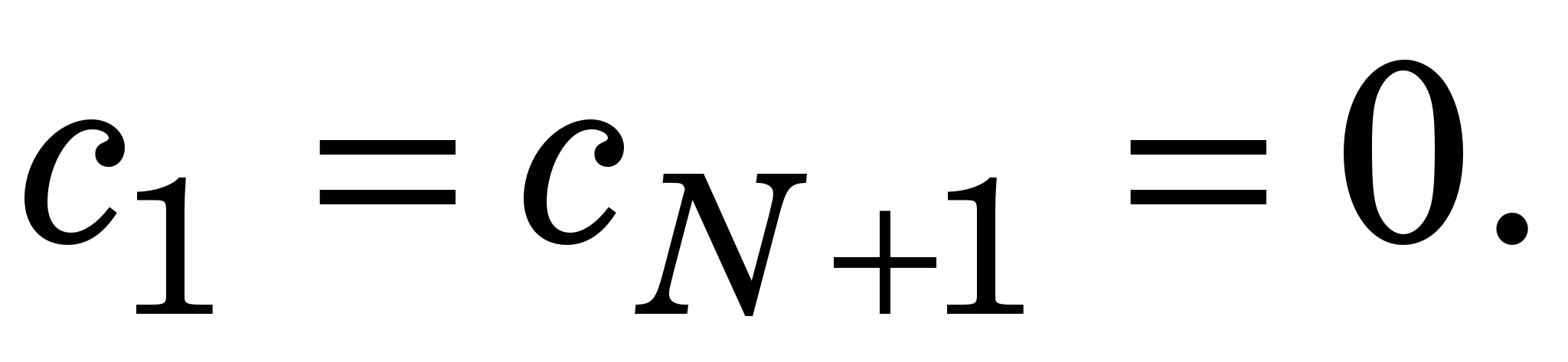
Приклад 1.2. Скориставшись табличними значеннями у(0)=0, у(1)=0.5, у(3)=1, у(2)= 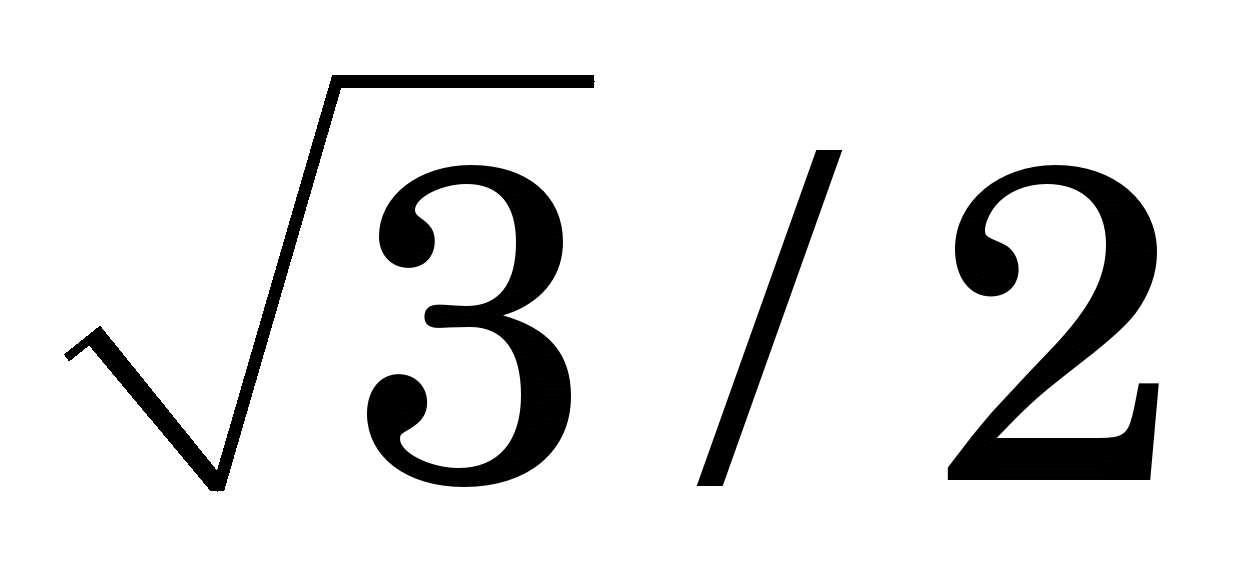 функції функції 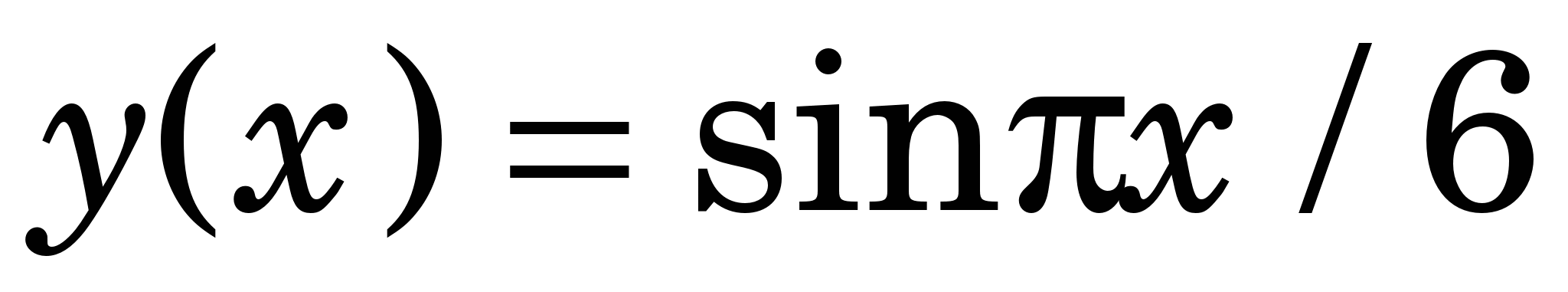 , знайдемо її значення у деяких точках відрізка [0, 1] за допомогою вільних кубічних сплайнів . , знайдемо її значення у деяких точках відрізка [0, 1] за допомогою вільних кубічних сплайнів .
Лістинг 1.2. Файл splncub:
// splncub
// Побудова ВКС на нерівномірній сітці
function [f] = ff(x); f = sin(%pi*x/6) endfunction;
// Задана функція
function [ac] = spln3(n,na,xx,yy);
// Функція spln3 обчислення коефіцієнтів ВКС
c(1) =0; aa(1)=0; na1=na+1; n1=n+1; c(n1)=0; m=n-1;
for i=1:n h(i)=xx(i+1)-xx(i); end;
for i=2:n
aa(i-1)=h(i-1); bb(i-1)=-2*(h(i-1)+h(i));
cc(i-1)=h(i); ayp = yy(i+1); ay0 = yy(i);
aym = yy(i-1);
dd(i-1)=((ayp-ay0)/h(i)-(ay0-aym)/h(i-1))*3
end;
// Обчислення коефіцієнтів с ВКС
[z] = algprog(na1,aa,bb,cc,dd);
// Формування масиву ac(n,4)коефіцієнтів ВКС
for i=1:m c(i+1)=z(i); end;
for i=1:n
// ac(i,1) – коефіцієнти а ВКС
ac(i,1)=yy(i); ayp = yy(i+1); ay0 = yy(i);
// ac(i,2) – коефіцієнти b ВКС
ac(i,2)=(ayp-ay0)/h(i)-...
h(i)*(c(i+1)+c(i)*2)/3
// ac(i,3) – коефіцієнти с ВКС
ac(i,3)=c(i)
// ac(i,4) – коефіцієнти d ВКС
ac(i,4)=(c(i+1)-c(i))/(3*h(i))
end;
endfunction;
// Розв’язання СЛАР алгебричною прогонкою
function [x] = algprog(n1,a,b,c,d);
n=n1-1; k(1)=0; h(1)=0; c(n)=0;
a(1)=0; k(n1)=0; x(n1)=0;
for i=1:n
ai =a(i);
zn =b(i)-ai*k(i);
k(i+1)=c(i)/zn;
h(i+1)=(ai*h(i)-d(i))/zn
end;
j=n1;
for i=1:n
j =j-1; x(j)=k(j+1)*x(j+1)+h(j+1)
end;
endfunction;
function [s,y,xd] = splncub(n,M,N,a,b,xd);
// Функція splncub формування ВКС та у(х) у точках xd
h=(b-a)/(N-1);
// Знаходження заданої функції у вузлах інтерполяції
for i=1:N
xx(i)=a+(i-1)*h; yy(i)=ff(xx(i));
end;
// Обчислення ВКС у вузлах інтерполяції
na=n-1;
// Обчислення коефіцієнтів ВКС за допомогою spln3
[ac] = spln3(n,na,xx,yy);
for j=1:M
xj=xd(j); x(j)=xj;
// Установлення підвідрізка розташування точки xj
for i=1:n
if(xj>=xx(i)&xj
k=i;
break;
end
end;
// Обчислення ВКС у точці xj
ss=ac(k,4); t=xj-xx(k);
for i=1:n
ss=ss*t+ac(k,4-i)
end;
// Формування значень ВКС та у(х) у точках масиву xd
s(j)=ss;
y(j)=ff(xj);
end;
// Перетворення векторів на матриці-рядки
y=y.'; s=s.';
endfunction;
// main program
// Координат точок для таблиць і графіків
xd=[0,0.5,1,1.5,2.,2.5,3];
// Коментар до фактичних параметрів функції splncub
//[s,y,xd] = splncub(n,M,N,a,b,xd);
[s,y,xd] = splncub(3,7,4,0,3,xd)
// Побудова графіків заданої функції та ВКС
x=xd.';
plot(x,s,'k+',x,y,'k-'); xgrid();
xtitle(' S=S(X) Y=Y(X)','X','S Y');
legend(' S=S(X) ',' Y=Y(X)',4,%t);
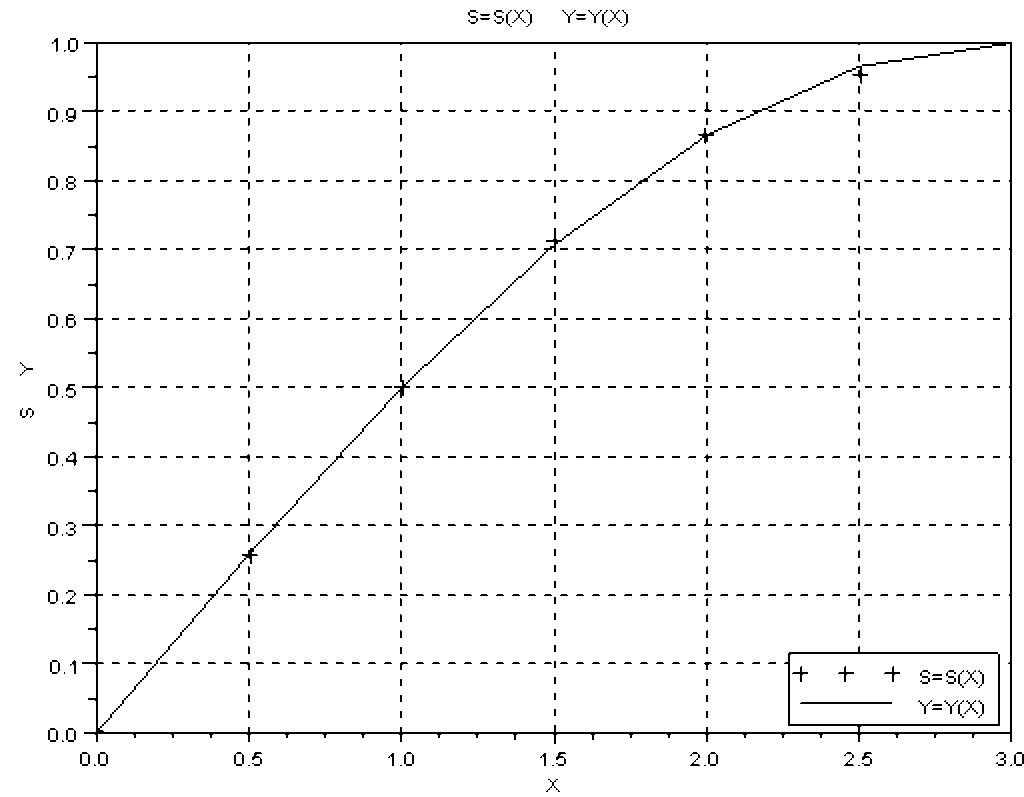
Результати виконання splncub
у табличному вигляді:
x = 0. 0.5 1. 1.5 2. 2.5 3.
y = 0. 0.2588190 0.5 0.7071068 0.8660254 0.9659258 1.
s = 0. 0.2575962 0.5 0.7104646 0.8660254 0.9528684 1.
графічному вигляді:
Оскільки ІПН забезпечує зручну апроксимацію лише на невеликому відрізку, тобто на декількох вузлах інтерполяції, то якщо для знаходження ВВП потрібно мати єдину апроксимувальну функцію 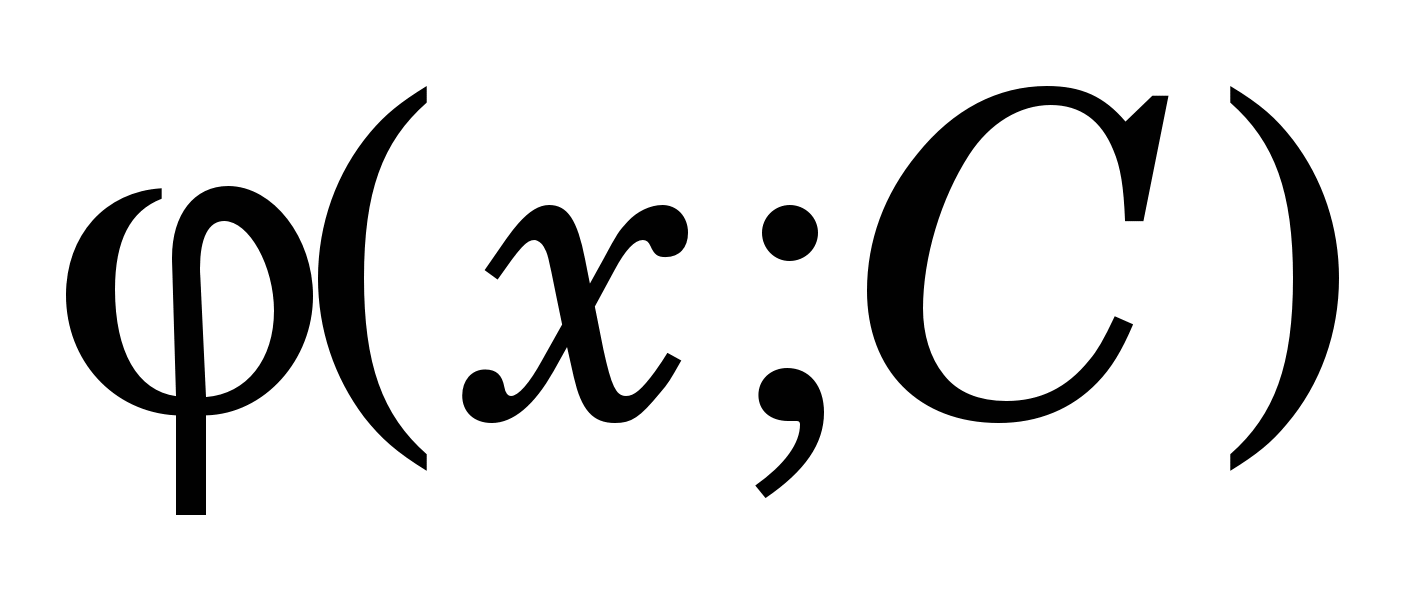 на значному відрізку або ж коли значення заданої функції y(х) знайдено неточно, вдаються, зокрема, до дискретного середнього квадратичного наближення (ДСКН) або методу найменших квадратів (МНК), в якому ВВП C визначають із такої умови: на значному відрізку або ж коли значення заданої функції y(х) знайдено неточно, вдаються, зокрема, до дискретного середнього квадратичного наближення (ДСКН) або методу найменших квадратів (МНК), в якому ВВП C визначають із такої умови:
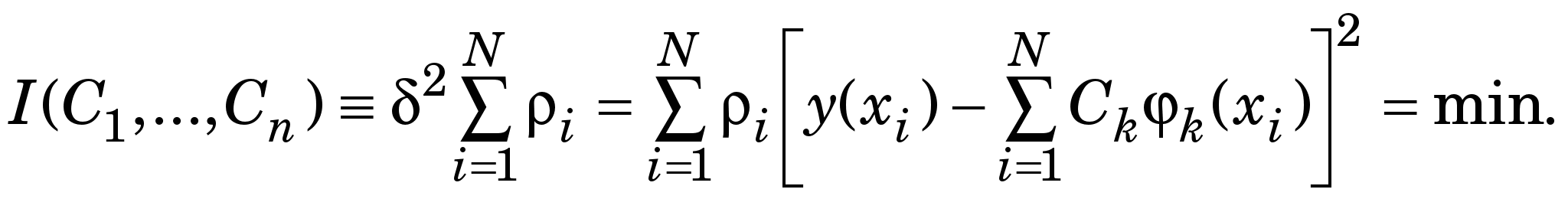 (1.2) (1.2)
Прирівнявши до нуля частинні похідні від 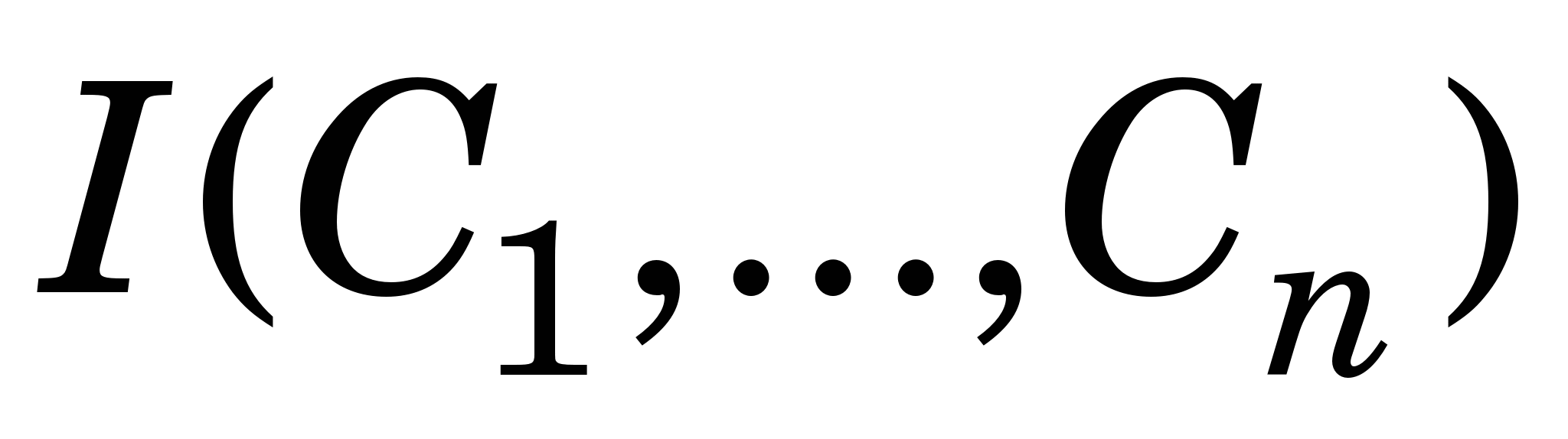 за всіма складовими за всіма складовими  дійдемо такої системи лінійних алгебричних рівнянь для їх визначення: дійдемо такої системи лінійних алгебричних рівнянь для їх визначення:
 (1.3) (1.3)
де 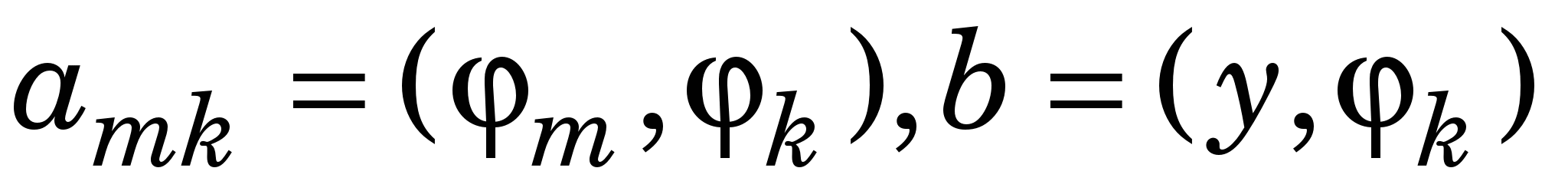 [ [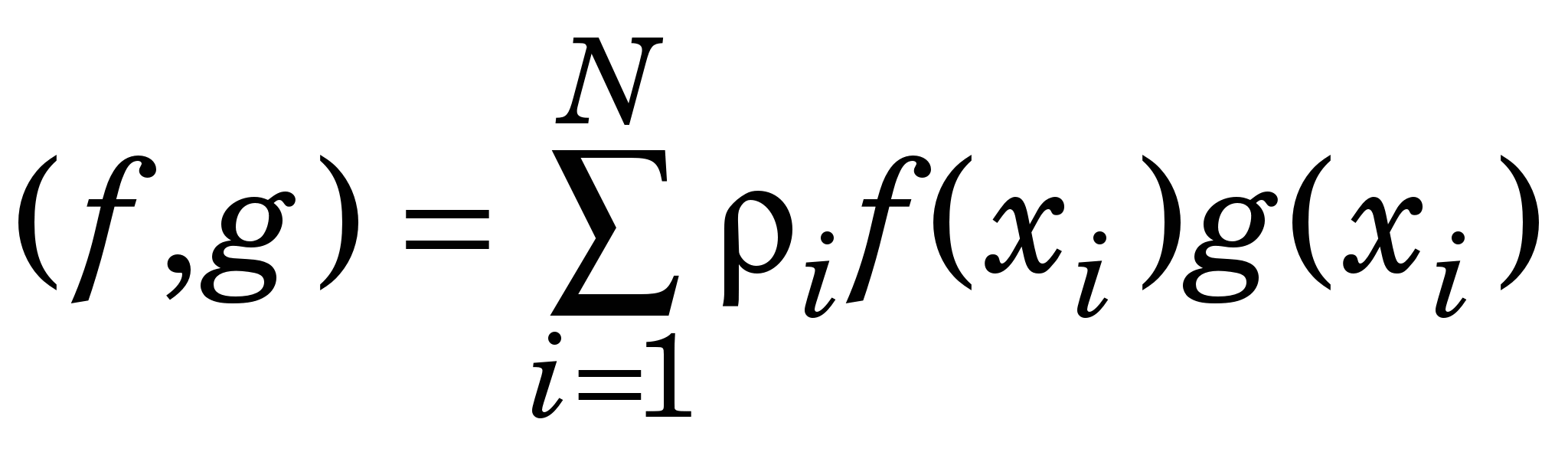 ]. ].
За умови лінійної незалежності  визначник (1.3) ненульовий, тобто дискретне середнє квадратичне наближення існує і воно єдине. визначник (1.3) ненульовий, тобто дискретне середнє квадратичне наближення існує і воно єдине.
Оптимальне число коефіцієнтів апроксимації  визначають, беручи n=1, коли, напевне, дискретне середнє квадратичне відхилення (ДСКВ) визначають, беручи n=1, коли, напевне, дискретне середнє квадратичне відхилення (ДСКВ)
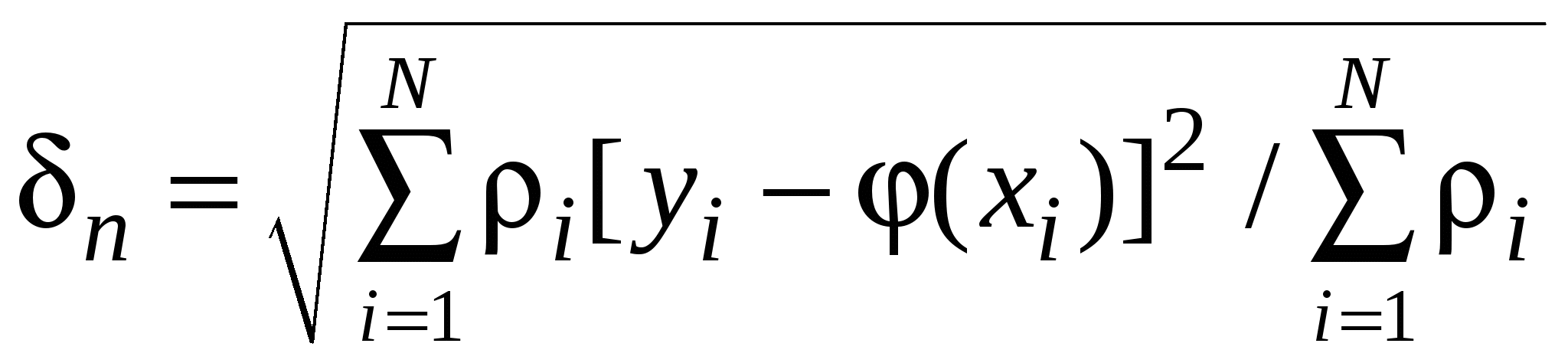 (1.4) (1.4)
 суттєво більше суттєво більше 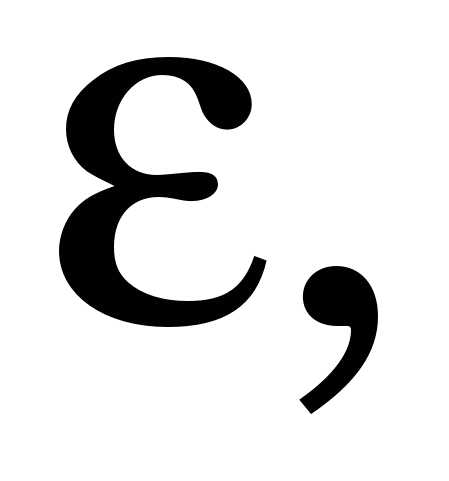 і збільшують число коефіцієнтів n доти, доки не почне виконуватись умова і збільшують число коефіцієнтів n доти, доки не почне виконуватись умова 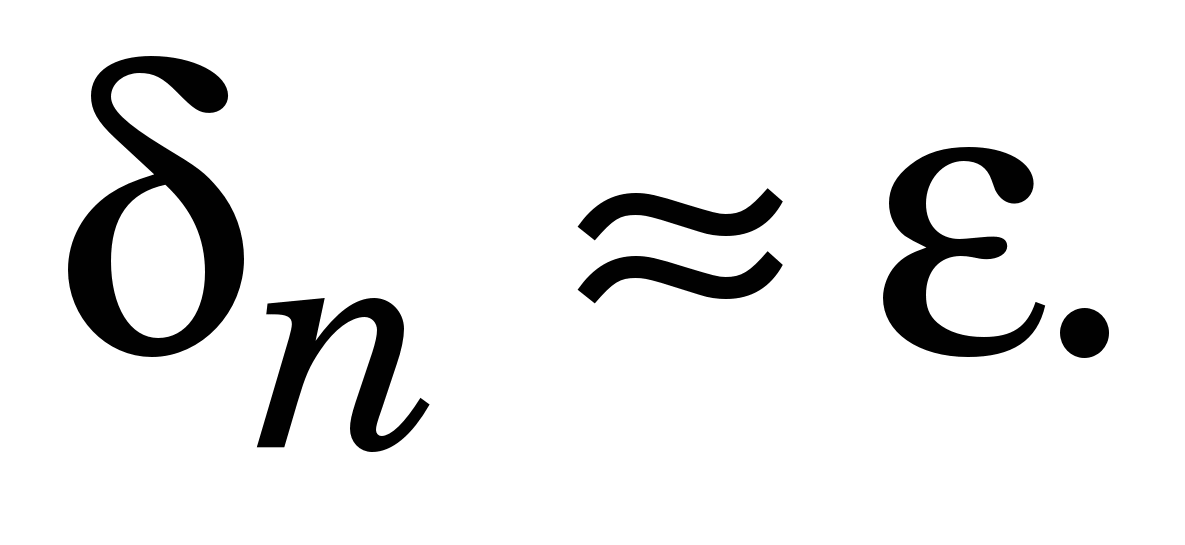 Якщо n суттєво менше N, то вираз (x) вибрано вдало. Якщо ж Якщо n суттєво менше N, то вираз (x) вибрано вдало. Якщо ж 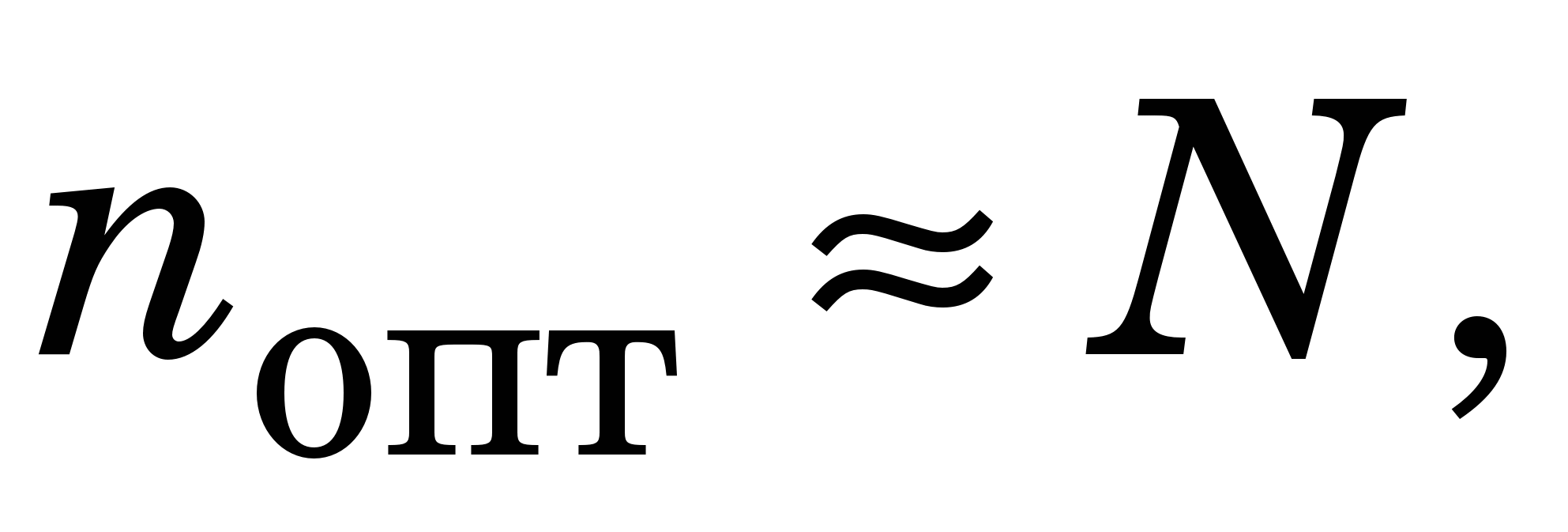 то апроксимувальну функцію (x) потрібно взяти в іншому вигляді. то апроксимувальну функцію (x) потрібно взяти в іншому вигляді.
Приклад 1.3. Знайдемо коефіцієнти квадратичної апроксимувальної функції 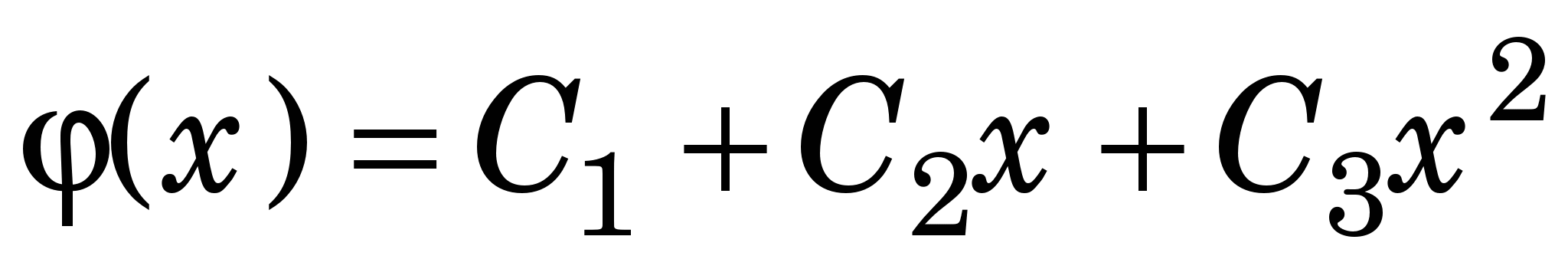 для функції для функції 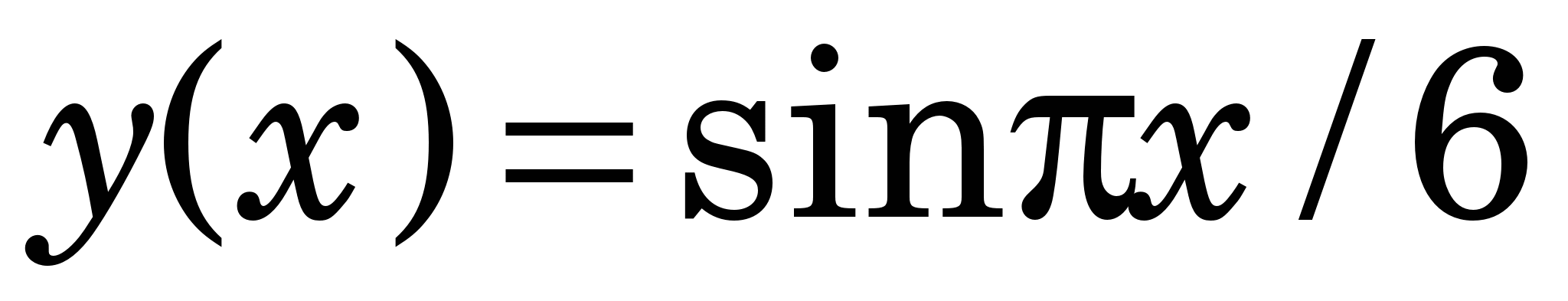 за допомогою МНК, застосовуючи вузли за допомогою МНК, застосовуючи вузли 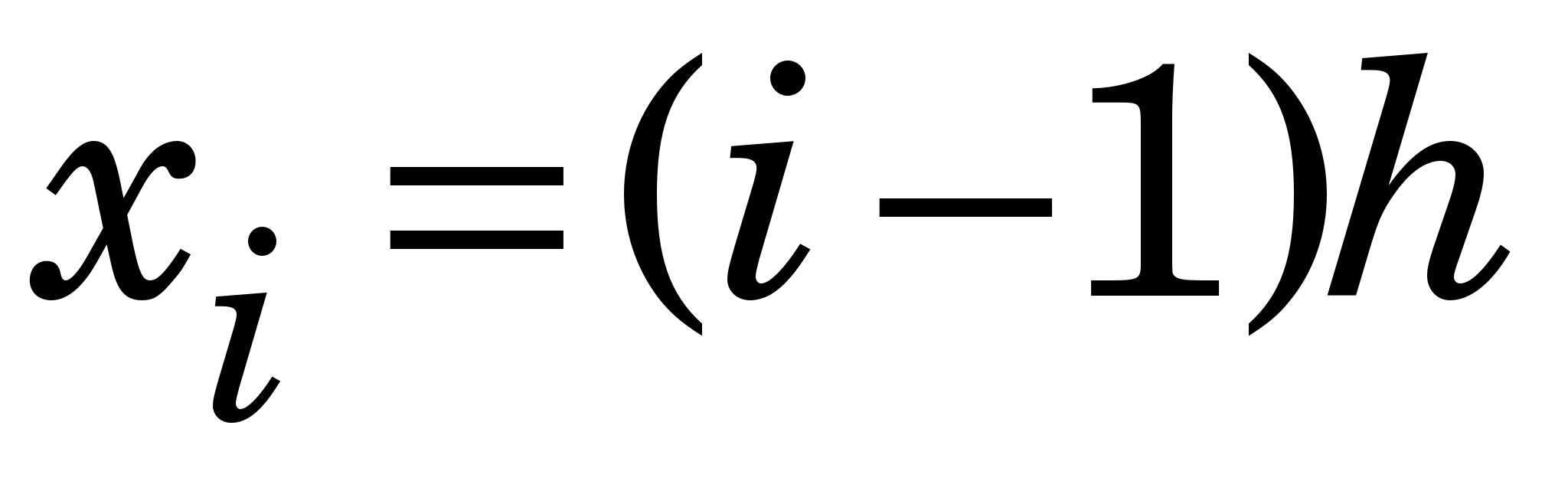 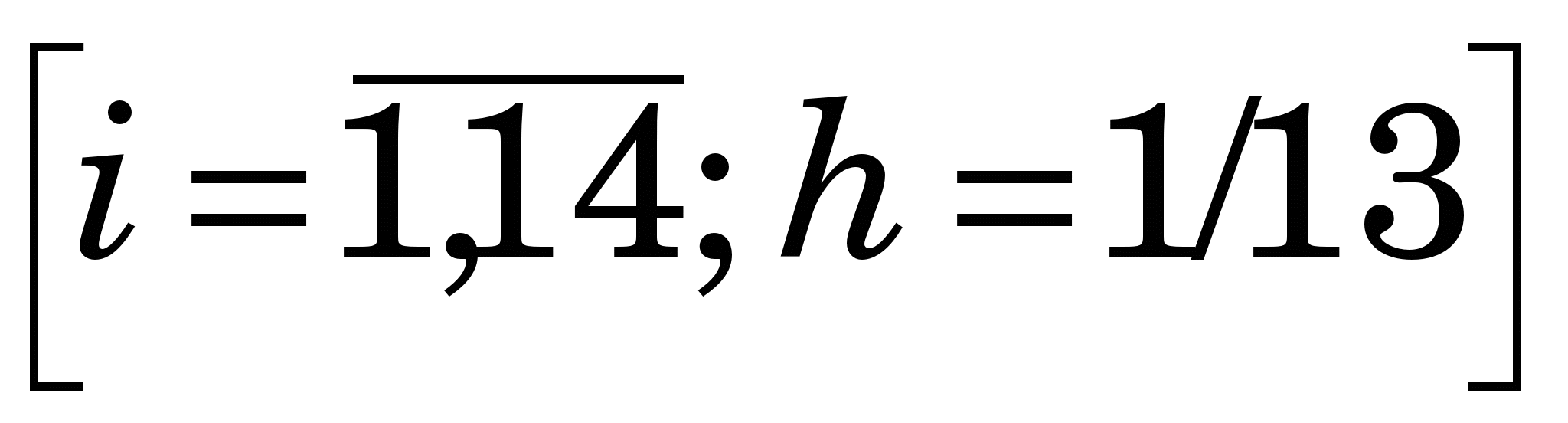 відрізка [0, 3], та обчислимо її наближені значення у деяких точках та ДСКВ. відрізка [0, 3], та обчислимо її наближені значення у деяких точках та ДСКВ.
Лістинг 1.3. Файл mnk:
// mnk
// Побудова апроксимувальної функції fi МНК та ДСКВ
function [f] = ff(x); f = sin(%pi*x/6) endfunction;
// Задана функція
function [dskv,C,y,fi,x] = mnk(n,N,M,a,b);
h=(b-a)/(N-1);
m=n+1;
// Обчислення вузлів та значень у(х) для МНК
for i=1:N
xx(i)=a+(i-1)*h; yy(i)=ff(xx(i));
end;
// Формування проміжних масивів для побудови А і В
n2=n*2; n1=n+1;
for j=1:n2
s=0;
for i=1:N
s=s+xx(i)^j;
end;
p(j)=s
end;
for i=1:n1
j1=1+(i-1)*n1; j2=i*n1;
k=i-j1-1;
for j=j1:j2
if (j==1) then
d(1)=N
end;
if (j==1) then
d(j)=p(j+k)
end;
end;
end;
// Формування вектора ПЧ В СЛАР (1.3)
s=0;
for i=1:N
s=s+yy(i)
end;
B(1)=s;
for i=2:n1
s=0;
for j=1:N
s=s+yy(j)*xx(j)^(i-1)
end;
B(i)=s
end;
// Формування матриці А СЛАР (1.3)
for i=1:m
for j=1:m
A(i,j)=d(i+m*(j-1));
end;
end;
// Розв’язання СЛАР (1.3) методом Гаусса
CC=rref([A B]); [NN,MM]=size(CC); C=CC(:,MM);
// Обчислення ДСКВ
dskv=0;
for i=1:N
xi=xx(i); fi =C(1);
for j=1:n
fi=fi+C(j+1)*xi^j;
end;
dskv=dskv+(fi-yy(i))^2;
end;
dskv=sqrt(dskv/N);
// Обчислення значень у(х) та АФ fi
h=(b-a)/(M-1);
for i=1:M
x(i)=a+(i-1)*h;
xi=x(i);
ffi=C(1);
for j=1:n
ffi=ffi+C(j+1)*xi^j;
end;
fi(i)=ffi;
y(i)=ff(xi);
end;
// Перетворення векторів на матриці-рядки
x=x.'; fi=fi.'; y=y.'; C=C.';
endfunction;
// main program
// Коментар до фактичних параметрів функції mnk
//[dskv,C,y,fi,x] = mnk(n, N,M,a,b)
[dskv,C,y,fi,x] = mnk(2,14,7,0,3)
// Побудова графіків заданої функції та АФ
plot(x,fi,'k.',x,y,'k-'); xgrid();
xtitle(' FI=FI(X) Y=Y(X)','X','FI Y');
legend(' FI=FI(X) ',' Y=Y(X)',4,%t);
Результати виконання mnk
у табличному (за збереження чотирьох значущих цифр за десятичною крапкою) вигляді:
x = 0. 0.5 1. 1.5 2. 2.5 3.
fi= -0.0186 0.2690 0.5105 0.7059 0.8552 0.9584 1.0156
y = 0. 0.2588 0.5 0.7071 0.8660 0.9659 1.
C = -0.0186 0.6212 - .0922 dskv = 0.0101
графічному вигляді:

2. Числове інтегрування
У практичних розрахунках, у тому числі й у задачах механіки, нерідко виникає потреба в обчисленні визначених інтегралів:
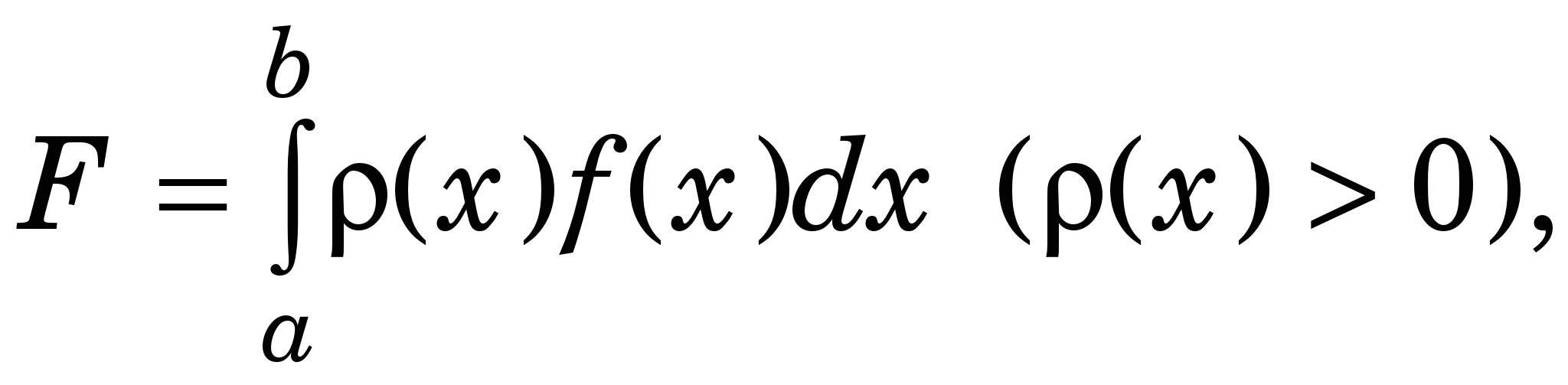 (2.1) (2.1)
де функція f(x) неперервна на відрізку [a, b], а вагова функція (x) неперервна на інтервалі (a, b).
За числового інтегрування (ЧІ) найчастіше підінтегральну функцію f(x) замінюють на алгебричний поліном, причому за умови 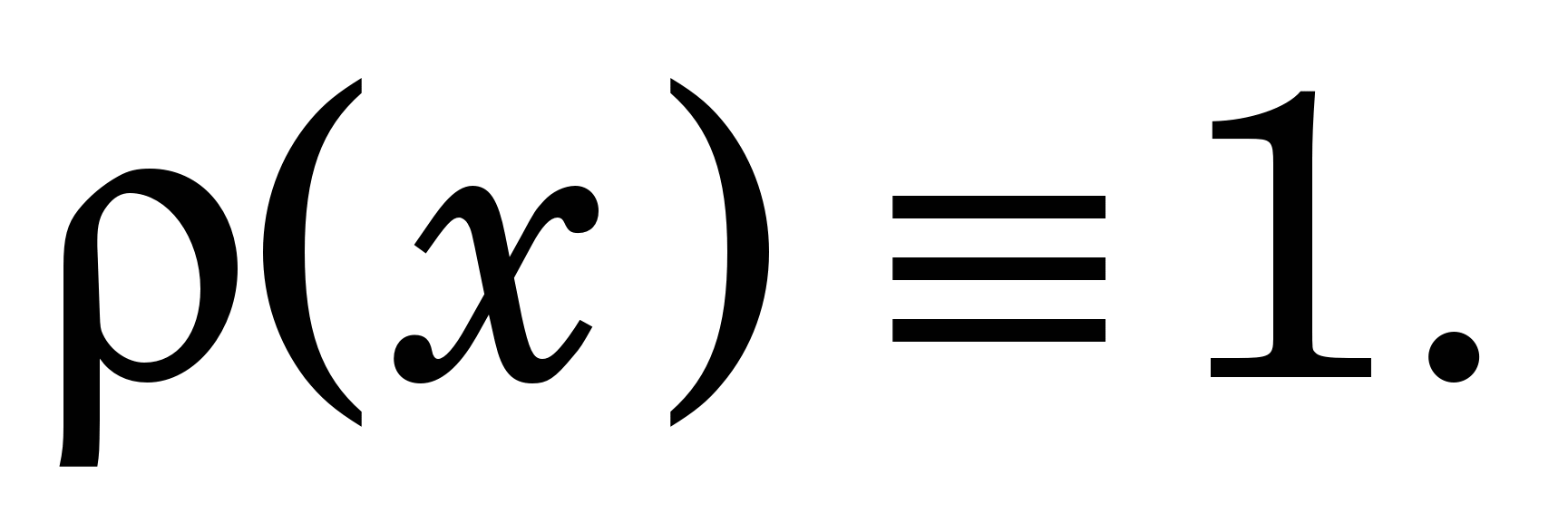
Узявши на відрізку [a, b] єдиний вузол у квадратурній формулі (КФ) 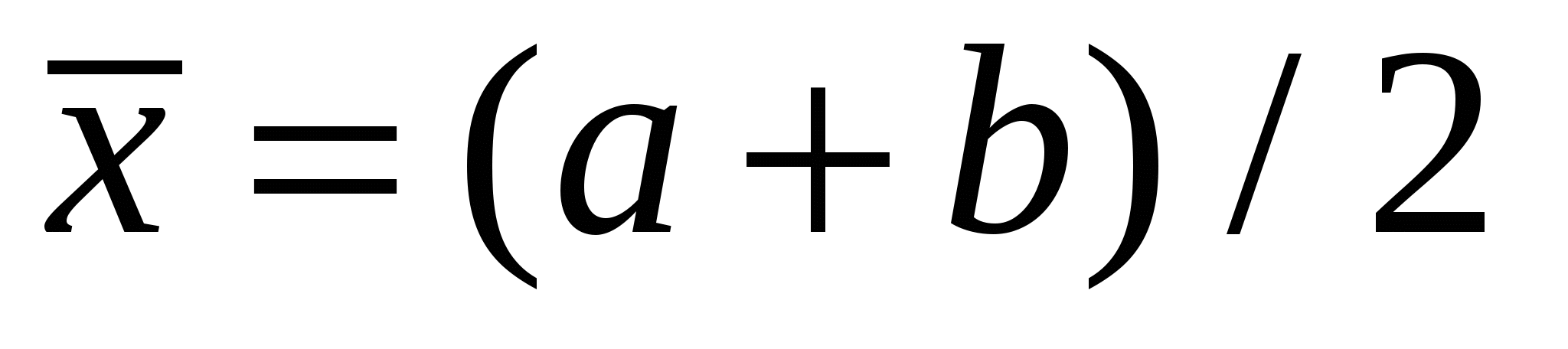 , тобто апроксимуючи підінтегральну функцію f(x) сталою f( , тобто апроксимуючи підінтегральну функцію f(x) сталою f(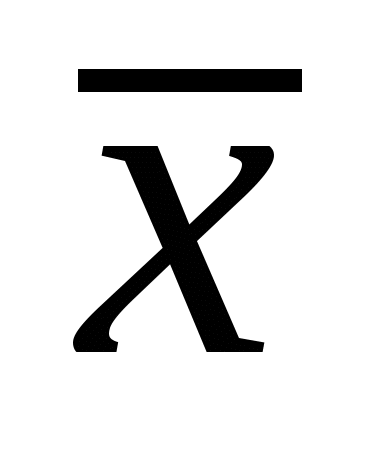 ), матимемо КФ середніх (ФС) ), матимемо КФ середніх (ФС) 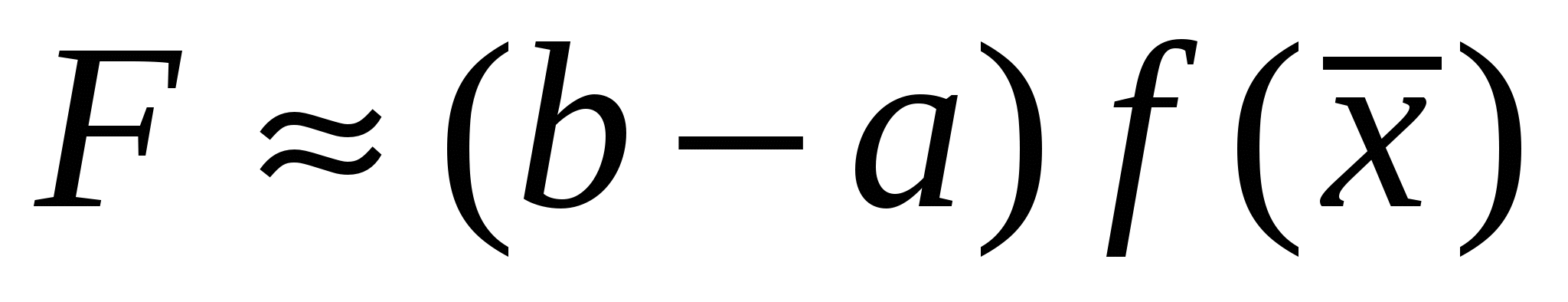 . .
Природно, що точність ФС для довільної f(x) можна підвищити, скориставшись детальнішою сіткою 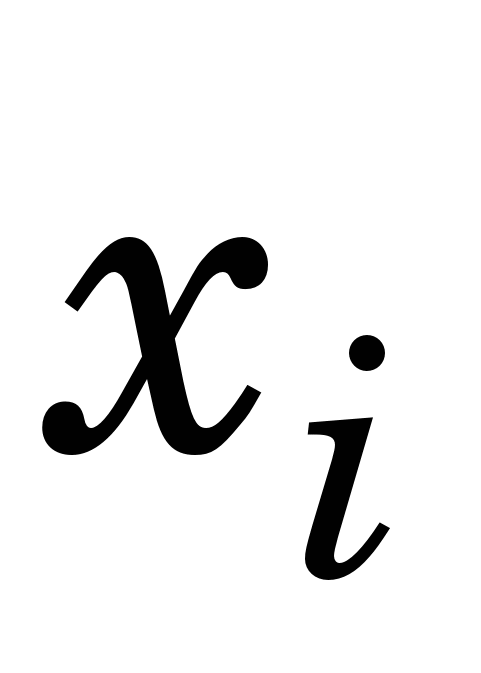 . Якщо . Якщо 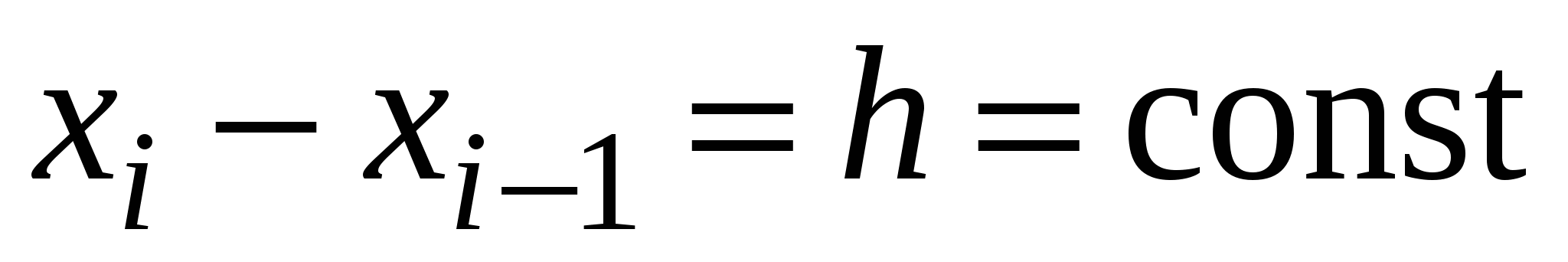 (рівномірна сітка), матимемо (рівномірна сітка), матимемо
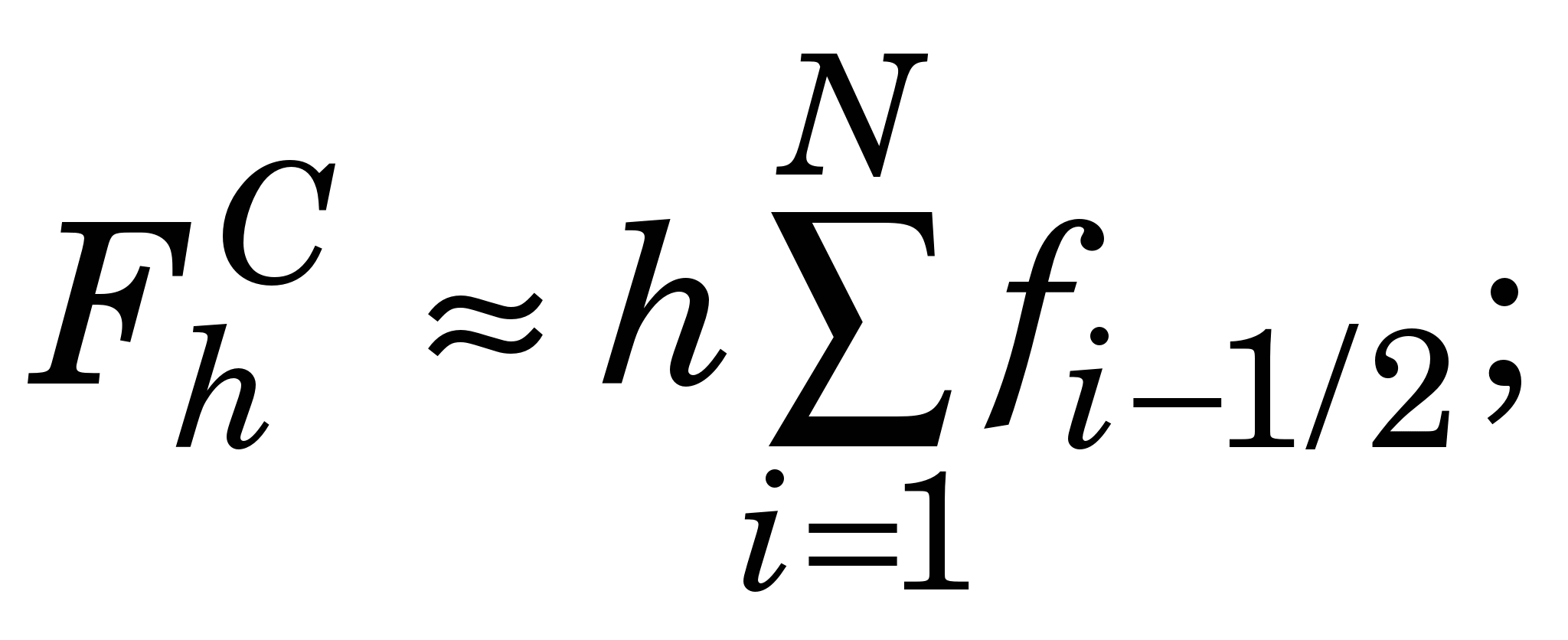 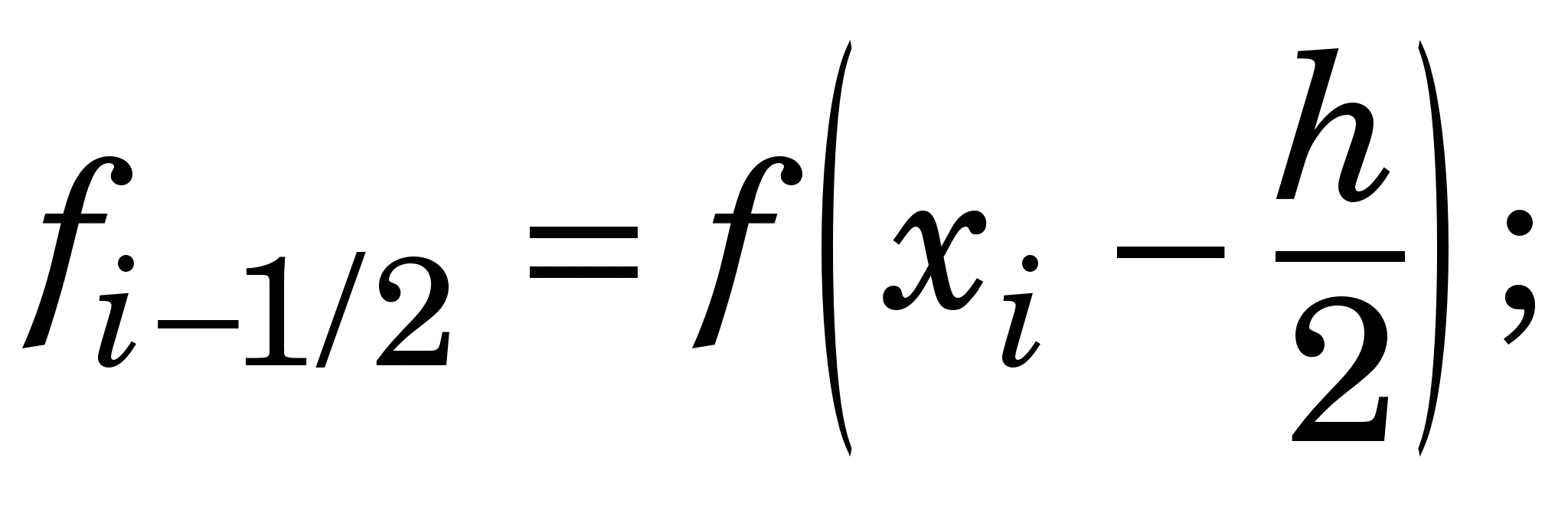 (2.2) (2.2)
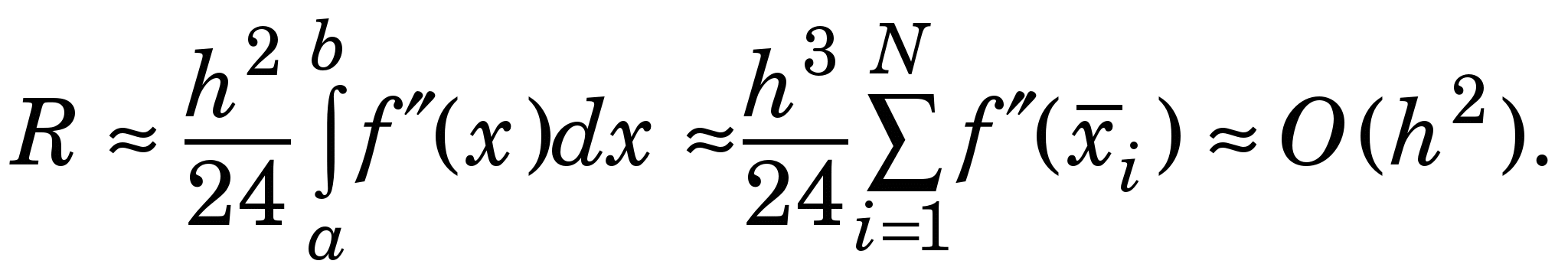 (2.3) (2.3)
Наведені оцінки R справедливі, якщо неперервна 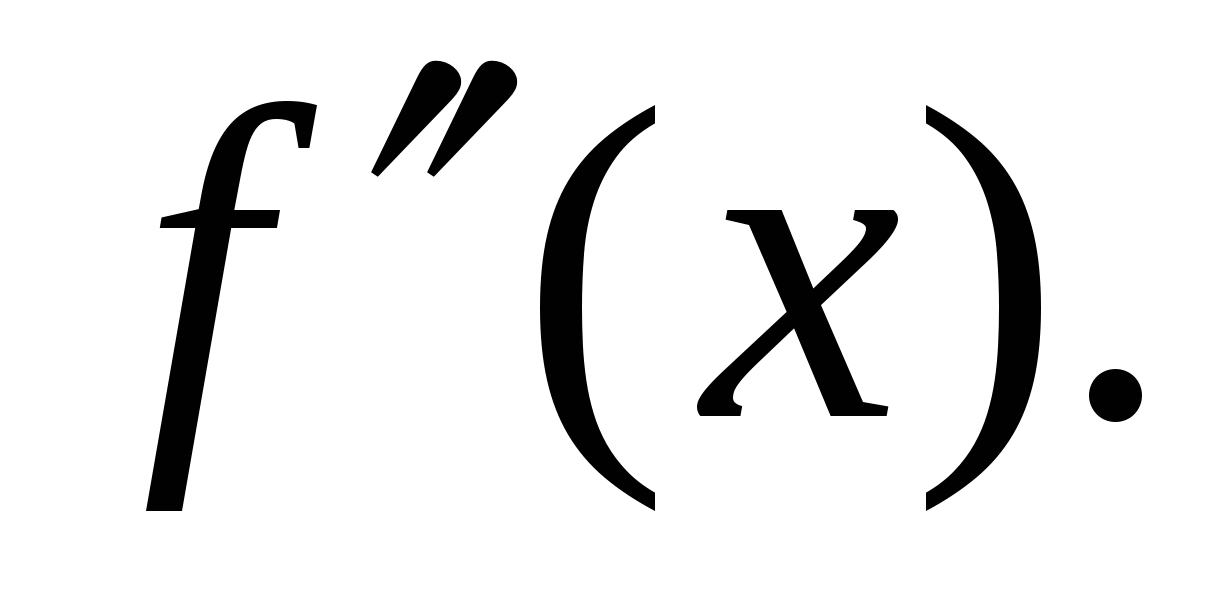
КФ трапецій (ФТ) одержують, замінивши функцію f(x) на відрізку [a, b] ІП першого степеня з вузлами   що відповідає заміні кривої f(x) на січну. На рівномірній сітці що відповідає заміні кривої f(x) на січну. На рівномірній сітці 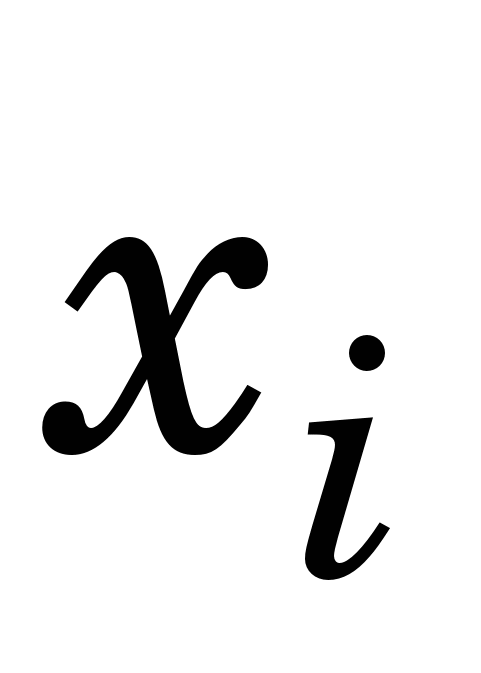 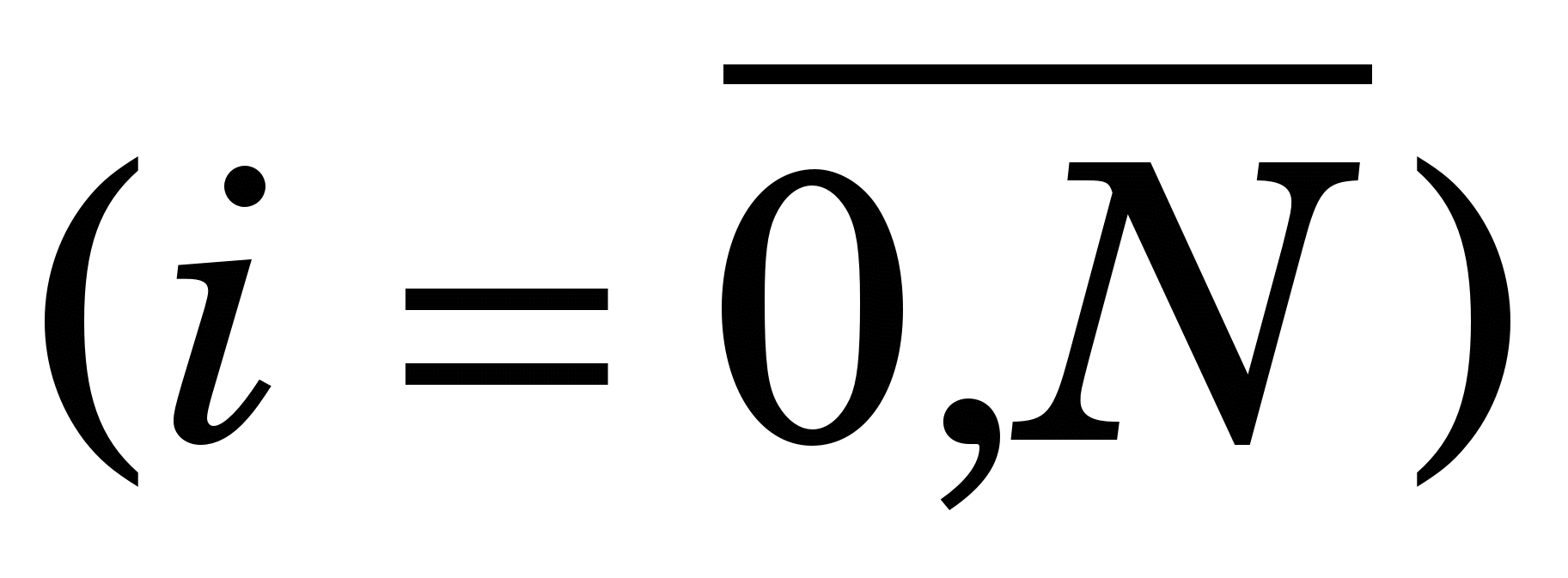 вона стає такою: вона стає такою:
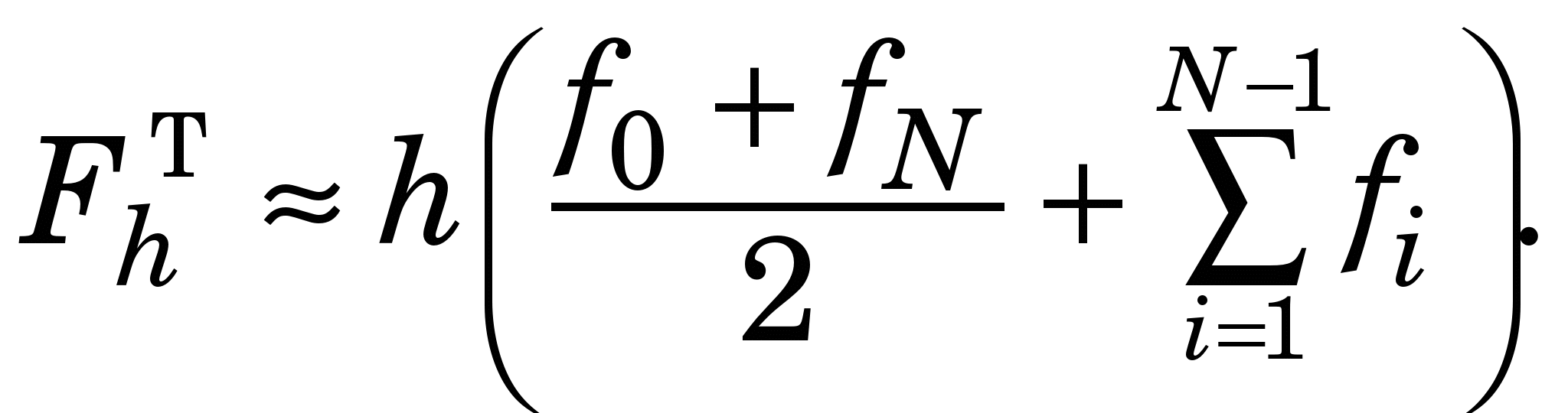 (2.4) (2.4)
Узагальнена КФ парабол (ФП) для рівномірної сітки має вигляд (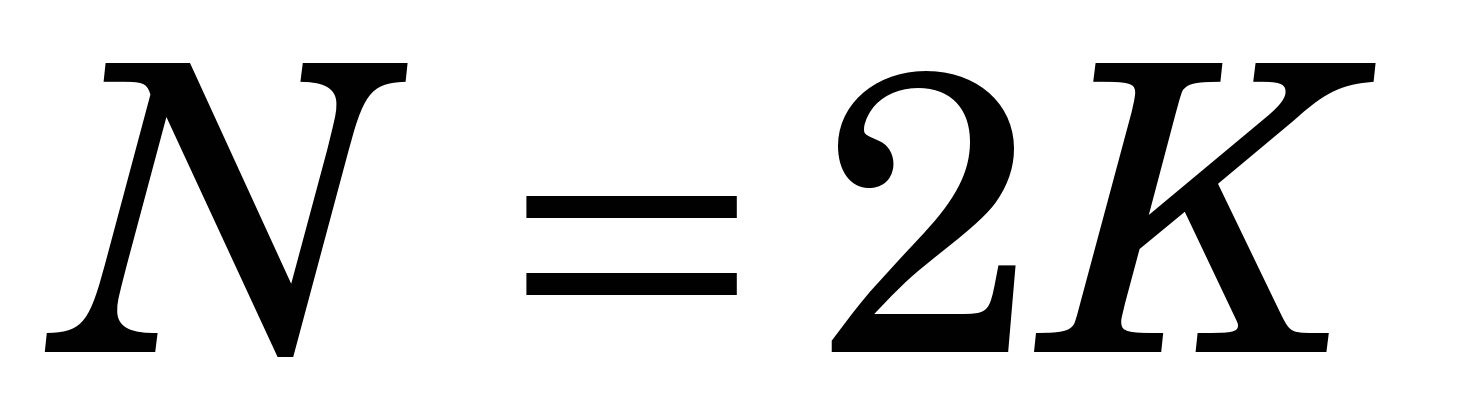 ) )
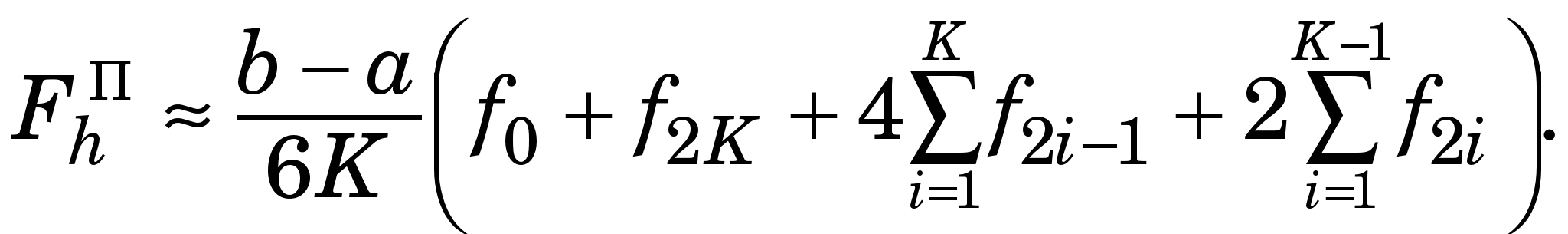 (2.5) (2.5)
Отже, ФП дає добру точність за відносно невеликого числа вузлів, якщо  не дуже велика. не дуже велика.
Для підвищення точності наведених КФ можна застосувати правило Рунге, якщо точне значення інтеграла F пов’язане з наближеним 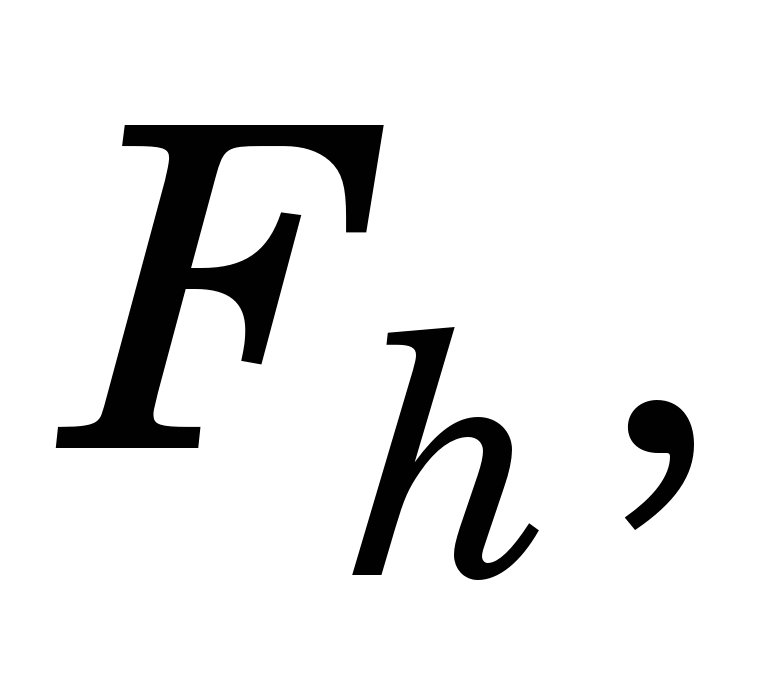 знайденим на сітці з кроком h: знайденим на сітці з кроком h:
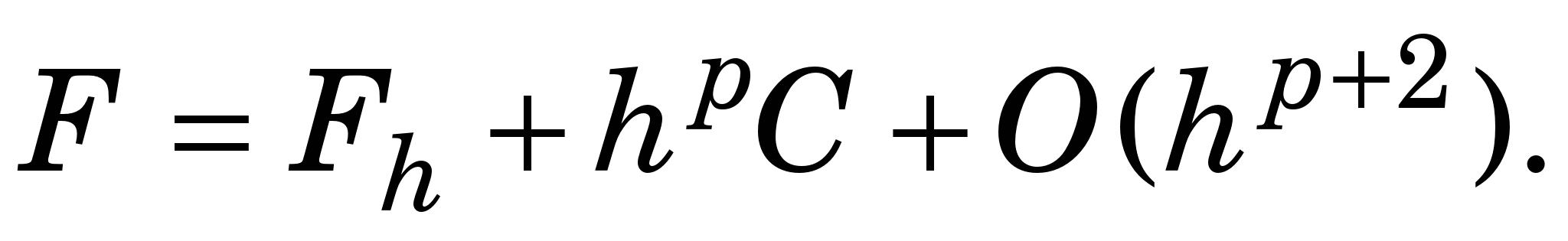
Для формул середніх (трапецій) і парабол відповідно  і і 
Перша формула Рунге для інтегрування — оцінка похибки ЧІ:
 (2.6) (2.6)
Тут  — наближене значення F, знайдене на сітці з кроком gh. — наближене значення F, знайдене на сітці з кроком gh.
Уточнене значення інтеграла знаходять за другою формулою Рунге:
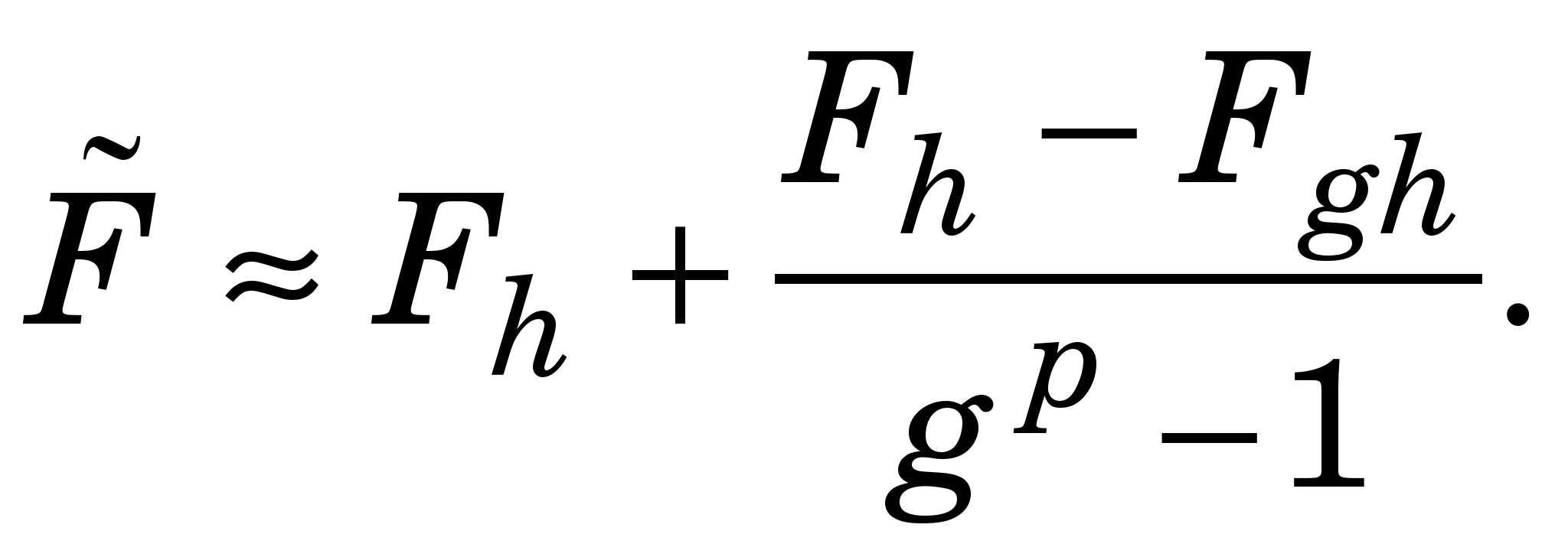 (2.7) (2.7)
Приклад 2.1. Скориставшись значенням підінтегральної функції ln(1+x) на відрізку [0, 1] f(0)=0, знайдемо за КФ середніх, трапецій та парабол наближені значення інтеграла  . .
Лістинг 2.1. Файл qfpr:
// qfpr
//Підінтегральна функція (ПФ)
function [f] =ff(x);
f = log(1+x)
endfunction;
// Обчислення інтеграла за різними КФ
function [trap,ser,par] = trapserpar(a,b,N);
h=(b-a)/N; // Крок сітки
// Формування значень ПФ для КФ середніх
for i=1:N
xi=a+(i-0.5)*h; y(i)=ff(xi)
end;
// КФ середніх
ser=0;
for i=1:N ser=ser+y(i); end;
ser=ser*h;
// Формування значень ПФ для КФ трапецій та парабол
N1=N+1;
for i=1:N1
xi=a+(i-1)*h; y(i)=ff(xi)
end;
// КФ трапецій
trap=(y(1)+y(N1))/2;
for i=2:N
trap=trap+y(i)
end;
trap=trap*h;
// КФ парабол
K=N/2; s1=y(1)+y(N1); s2=0; s4=0;
for i=2:K
s2=s2+y(i*2-1)
end;
for i=1:K
s4=s4+y(i*2)
end;
par=(s1+s2*2+s4*4)*h/3
endfunction;
// Уточнення КФ за правилом Рунге
function [Ftrap,Fser,Fpar] = qfpr(a,b,N);
[trap1,ser1,par1] = trapserpar(a,b,N);
[trap2,ser2,par2] = trapserpar(a,b,N*2);
Ftrap=trap1+(trap1-trap2)/3; Fser=ser1+(ser1-ser2)/3;
Fpar=par1+(par1-par2)/15
endfunction;
// main program
// N - парне
// Точне значення інтеграла F = 0.3862944
// Коментар фактичних параметрів функції qfpr
//[Ftrap,Fser,Fpar] = qfpr(a,b,N);
[Ftrap,Fser,Fpar] = qfpr(0,1,4)
Результати виконання qfpr
Fpar = 0.3862574 Fser = 0.3879113 Ftrap = 0.3830514
|
|
|
 Скачать 0.83 Mb.
Скачать 0.83 Mb.