Посібник по ЧМ. Наближення функцій
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Структура лабораторної роботи та приклад її оформлення (Окрема стор. - 1) Міністерство освіти і науки, молоді та спорту України Дніпропетровський національний університет імені Олеся Гончара Механіко-математичний факультет Кафедра обчислювальної механіки та міцності конструкцій Л А Б О Р А Т О Р Н А Р О Б О Т А з ч и с е л ь н и х м е т о д і в Інтерполяція функції поліномом Ньютона Шифр 88888 Виконавець студент групи (код групи) (Прізвище й ініціали) Керівник (посада викладача) (Прізвище й ініціали) Дніпропетровськ Рік виконання (наприклад, 2012) ================================================================= (З нової стор. - 2) З М І С Т Постановка задачі ................................................................................................................... 3 Реферат ................................................................................................................................... 4 Вступ ................................................................................................................................... 1. Інтерполяційний поліном Ньютона (ІПН) .............................................................. 2. Опис обчислювального алгоритму .......................................................................... 3. Обговорення результатів ............................................................................................ Висновки ............................................................................................................................. Список посилань ................................................................................................................ Додатки: .............................................................................................................................. А. Опис вихідних даних та результатів розрахунку ................................................... Б. Лістинг програми ....................................................................................................... В. Схема обчислювального алгоритму ......................................................................... ================================================================= (З нової стор. - 3) Постановка задачі Знайти наближене значення функції y(x) = 5*sіn x – 10*3-x у точках = 0.60 та х=0.6375, 1.1125 за допомогою ІПН (1.1), побудованого за її відомими трьома значеннями у точках x0=a=0.4, x1=0.875, x2=b=1.35 (k1 = 5, k2 = - 10, k3 = 2/9). Оцінити похибку інтерполяції в точці = 0.60 за формулою (1.2). Окрім того, знайти y() – P2() і порівняти з |r2()| . ================================================================= (З нової стор. - 4) Р Е Ф Е Р А Т Задача наближення функцій взагалі полягає в заміні аналітично або таблично заданої функції y(x) зручною для обчислень апроксимувальною функцією (x), яка б для всіх необхідних нам значень аргументу задовольняла співвідношення y(x) (x). Цієї мети досягають уведенням вектора вільних параметрів (невідомих коефіцієнтів) C=(C1,...,Cn) в (x) [тобто (x)= (x;C)] і його визначенням з прийнятої умови близькості функцій y(x) та (x). Звичайно, вважається, що у випадку табульованої функції y(x) її графік є плавна крива [1]. Інтерполяція Якщо за умову близькості (x) і y(x) взяти їх збіжність в n точках (вузлах інтерполяції) xі(), то C визначають як результат розв'язання такої системи алгебричних рівнянь (САР): (xі;C) = y(xі) (). (1) Це так звана лагранжова інтерполяція. Якщо компоненти вектора Сі () входять до виразу (xі;C) лінійно, тоді інтерполяцію називають лінійною, у протилежному випадку - нелінійною. Лінійна інтерполяція Задача істотно спрощується, якщо (x) має вигляд узагальненого полінома (x;C) = , (2) де k(x) - система лінійно незалежних функцій. Підставивши (2) до (1), одержимо для визначення C таку СЛАР: = y(xі) (). (3) Для єдиності розв'язку задачі інтерполяції визначник цієї СЛАР (3) не повинен перетворюватись на нуль (природно, серед вузлів інтерполяції не повинно бути збіжних). Найзручнішими для обчислень функцій є алгебричні поліноми k(x)=xk ( Про застосування та збіжність інтерполяції Окрім основної задачі інтерполяції (відновлення значення функції за відомими) її застосовують для тестування таблиць на наявність несистематичних похибок (друга ПР поводить тоді себе хаотично), субтабулювання (зменшення кроку існуючої таблиці) та оберненої інтерполяції (знаходження значення аргументу для заданого чи відомого значення функції). Похибку алгебричної інтерполяції можна зменшити двома шляхами - зберегти степінь полінома, а крок зменшити, або зберегти крок, збільшивши кількість використовуваних вузлів. У практичних розрахунках збільшення n небажане (бо призводить до збільшення похибки), тому для підвищення точності інтерполяції доцільно обмежитися 3 - 5 вузлами (точніше, вільними параметрами) і зменшити крок таблиці, не змінюючи n. Вступ Необхідність застосування наближення функцій виникає в механіці для обробки експериментальних даних або числового розв'язання задачі, тобто для відновлення значень деякої функції у точках, цікавих для нас, за відомими її значеннями. 1. Інтерполяційний поліном Ньютона Для побудови ІПН вводять так звані поділені різниці (ПР) , . Оскільки ПР мають вимірність похідних, то інколи їх використовують як наближені значення останніх. Якщо побудувати ПР полінома n-го степеня, можна, скориставшись умовами збіжності полінома з заданою функцією та її ПР у вузлах інтерполяції, одержати такий вираз для ІПН: y(x) y(x0)+ . (1.1) Наведений тут ІПН використовують у випадку таблиць зі змінним кроком. Похибку інтерполяції в точці х оцінюють за формулою |rn(x)| |y(x) – Pn(x)| = Mn+1 (x) / (n+1)! , (1.2) де Mn+1 = max |y(n+1)(x)| на відрізку [a,b]. Для обчислення ПР складають таблицю ПР функції y(x), а потім її наближені значення знаходять за формулою (1.1). 2. Опис обчислювального алгоритму Реалізуючи алгоритм знаходження ІПН за формулою (1.1) для зменшення необхідної пам'яті ЕОМ, розміщуємо значення ПР на місці попередньо знайдених значень вихідної функції y(x). Крім того, витрати машинного часу зменшаться, якщо ІПН знаходити за схемою Горнера. Оскільки значення ІПН обчислюють неодноразово, то цей процес оформлюємо у вигляді функції. 3. Обговорення результатів Із порівняння наведених у лістингу точних і наближених значень функції y(x) видно, що вони відрізняються третіми значущими цифрами [y()-P2()= 0.014], а значення похибки наближення |r2()| визначаємоза формулою (1.2), вона дорівнює 0.027 . ================================================================= (З нової стор.) Висновки Отже, ураховуючи п. 2 і 3, на практиці слід надавати перевагу ІПН, оскільки формула (1.1) дозволяє одержати прийнятні результати, а за збільшення кількості вузлів не потрібно перерахувати всі доданки у (1.1), до того ж порядок нумерації вузлів тут не має значення. ================================================================= (З нової стор.) Список посилань 1.Мусіяка, В.Г. Основи чисельних методів механіки[Текст]: підручник /В.Г. Мусіяка — К.: Вища освіта, 2004. — 240 с. 2.Мусіяка, В.Г. Практикум з обчислювальної механіки [Текст] /В.Г. Мусіяка. — Д.: РВВ ДНУ, 2006. — 64 с. ================================================================= (З нової стор.) Додатки А. Опис вихідних даних і результатів розрахунку Вихідні дані для побудови ІПН (вузли і значення в них заданої функції) xx=[ 0.4 ,0.875, 1.35 ]; yy=[-4.4968,0.0137,2.6093]; та координати точок для побудови таблиці й графіків заданої функції й ІПН xd=[0.4,0.6,0.6375,0.875,1.1125,1.35]. Результати виконання програми друкують в такому вигляді: x = 0.4 0.6 0.6375 0.875 1.1125 1.35 y = - 4.4968 - 2.3496 - 1.9881 0.01371 1.5382 2.6093 p = - 4.4968 - 2.3643 - 2.0022 0.01371 1.5509 2.6093 (З нової стор.) Б. Лістинг програми // ipn function [pln] = plnwt(n,xp,xx,yy); y=yy(n+1); for k=1:n n1=n-k+1; y=yy(n1)+y*(xp-xx(n1)); end; pln=y endfunction; function [p,y,x] = ipn(n,M,xx,yy,xd); deff('c = f(x)','c =5*sin(x)-10/exp(x*log(3))'); m=n+1; for k=1:m nt=n-k+1; for i=1:nt n1=n-i+1; n2=n1+1; yy(n2)=(yy(n2)-yy(n1))/(xx(n2)-xx(n1-k+1)); end end; for k=1:M xp=xd(k); p(k)=plnwt(n,xp,xx,yy); x(k)=xp; y(k)=f(xp); end; x=x.'; y=y.'; p=p.'; endfunction; // main program xx=[ 0.4, 0.875, 1.35]; yy=[-4.4968484,0.0137085,2.6093461]; xd=[0.4,0.6,0.6375,0.875,1.1125,1.35]; //[p,y,x] = ipn(n,M,xx,yy,xd) [p,y,x] = ipn(2,6,xx,yy,xd) plot(x,p,'k*',x,y,'k-'); xgrid(); xtitle(' P=P(X) Y=Y(X)','X','P Y'); legend(' P=P(X) ',' Y=Y(X)', 4, %t); Результати виконання ipn: у табличному вигляді: x = 0.4 0.6 0.6375 0.875 1.1125 1.35 y = - 4.4968 - 2.3496 - 1.9881 0.01371 1.5382 2.6093 p = - 4.4968 - 2.3643 - 2.0022 0.01371 1.5509 2.6093; графічному вигляді: 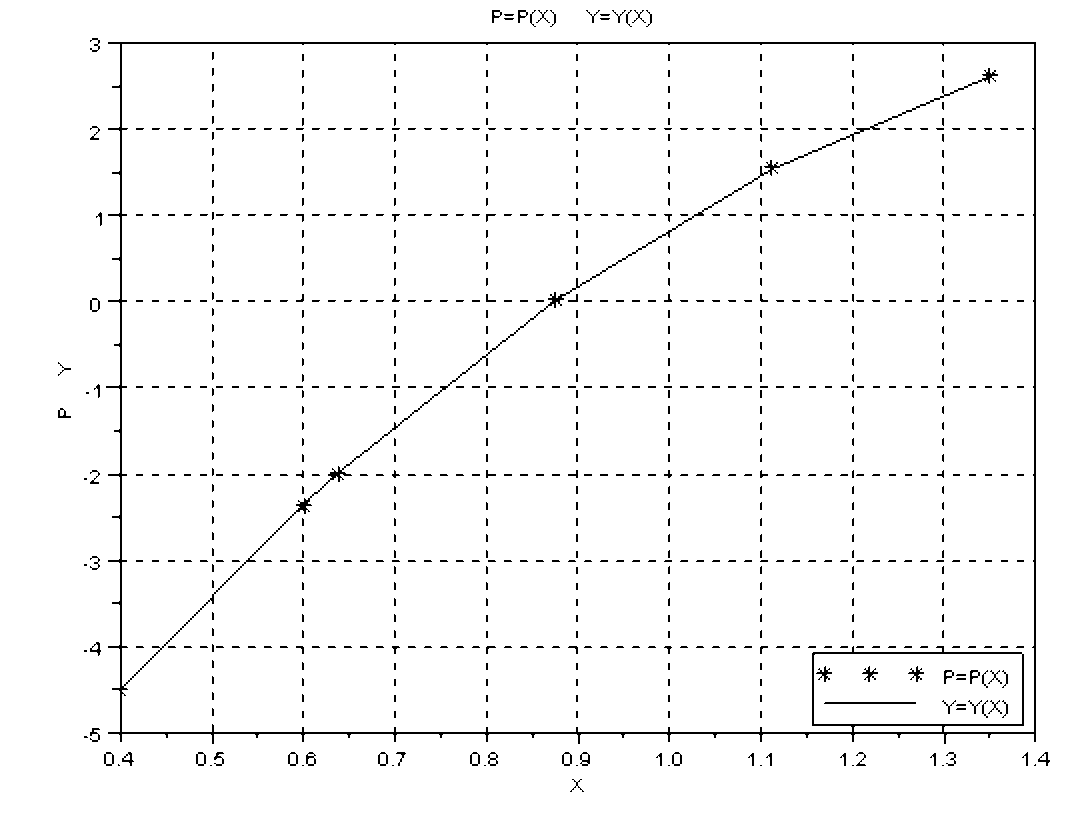 В. Схема обчислювального алгоритму 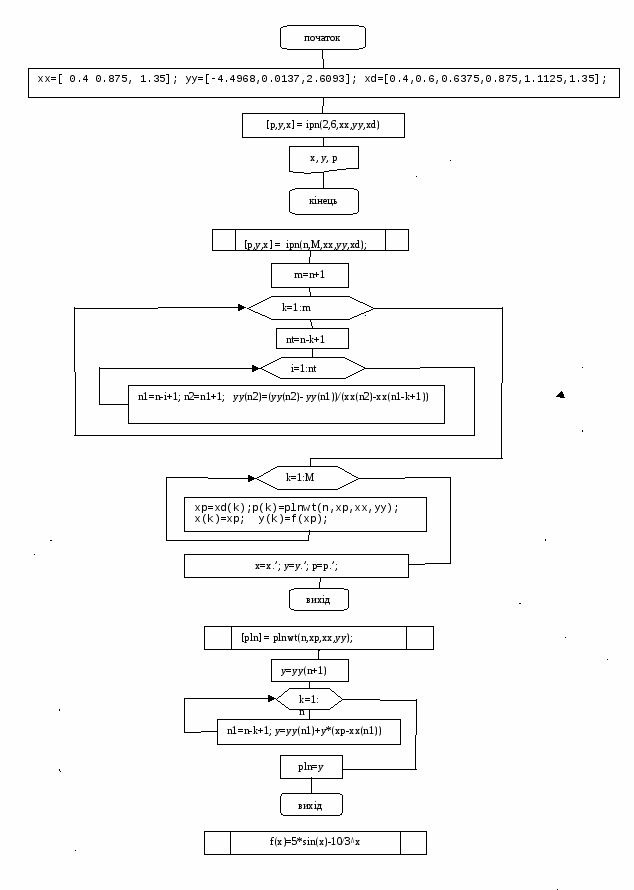 |
