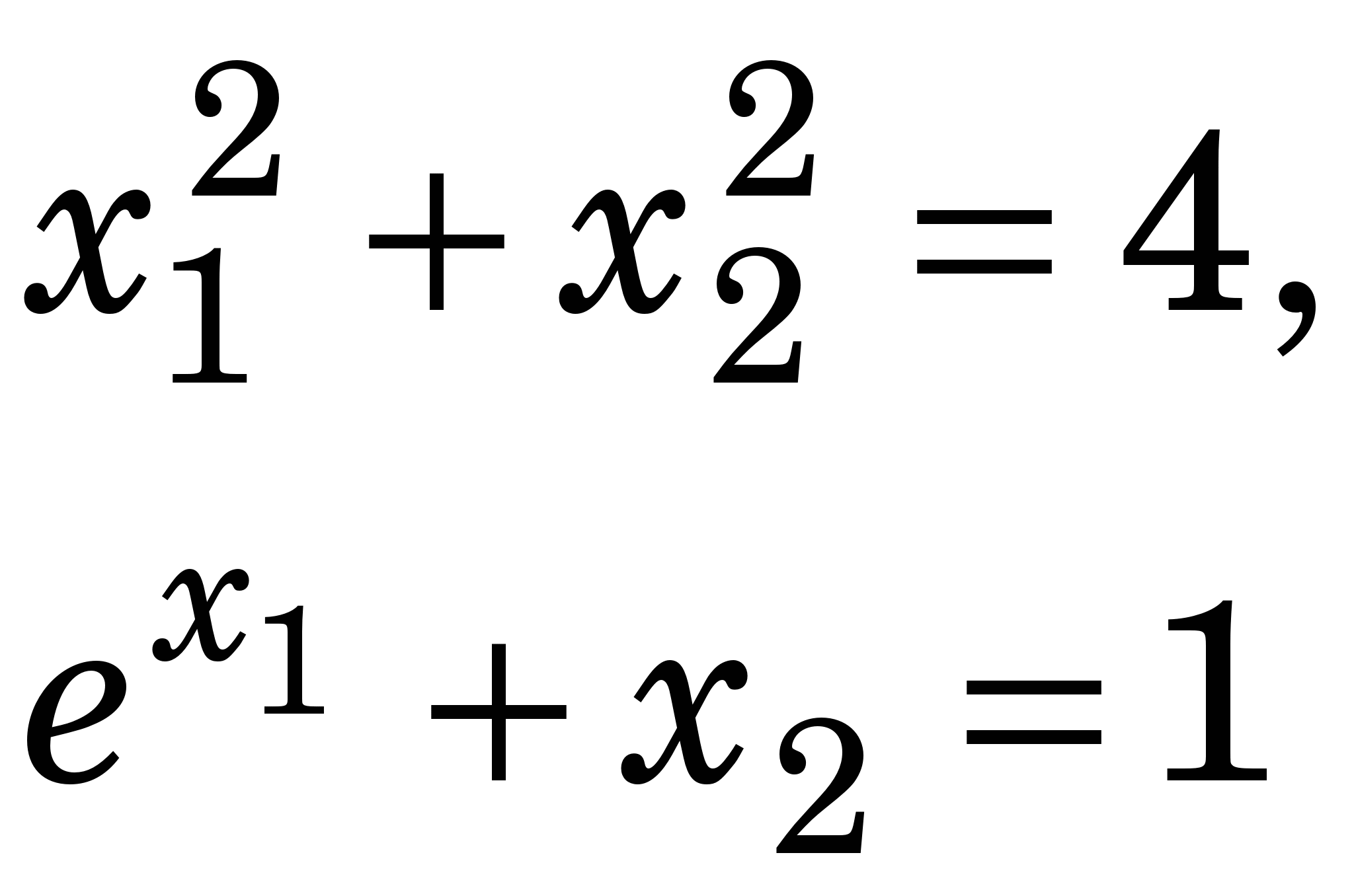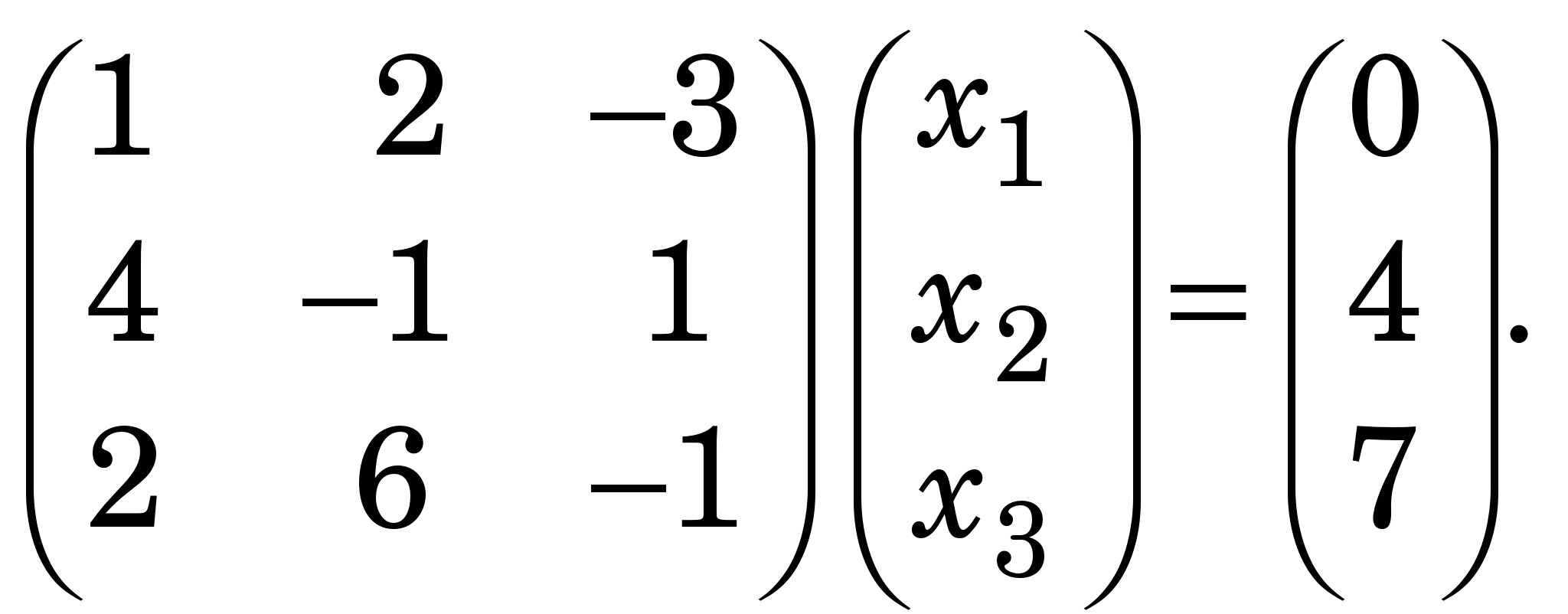|
|
Посібник по ЧМ. Наближення функцій
3. Нелінійні алгебричні рівняння
Розглянемо систему нелінійних рівнянь (СНР) з n невідомими:
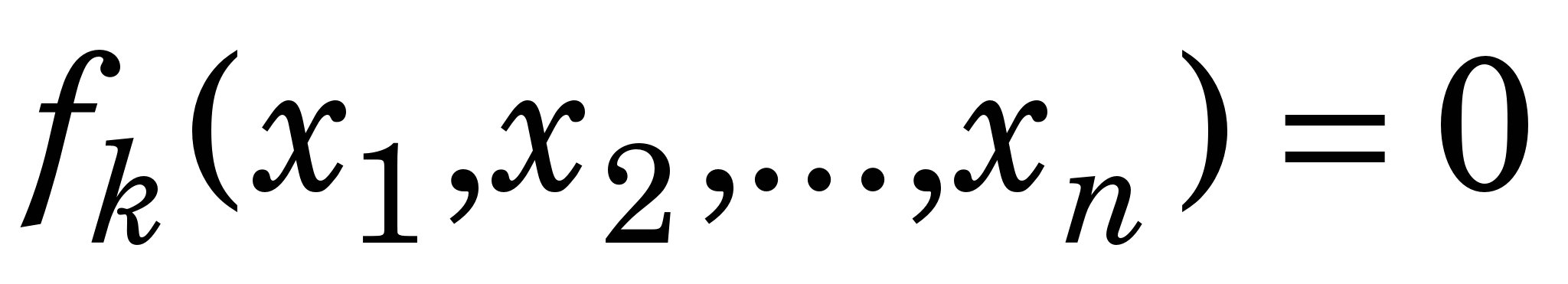 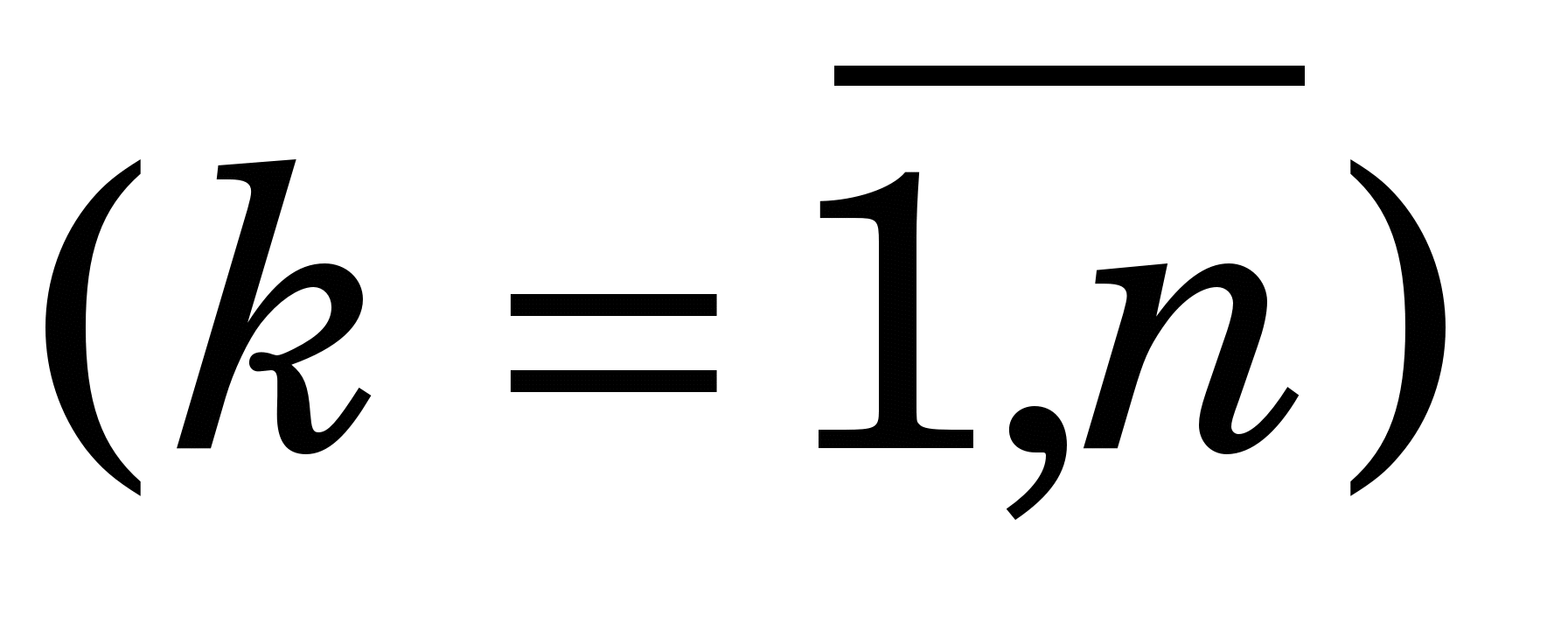 . (3.6) . (3.6)
Її можна записати у векторному вигляді:
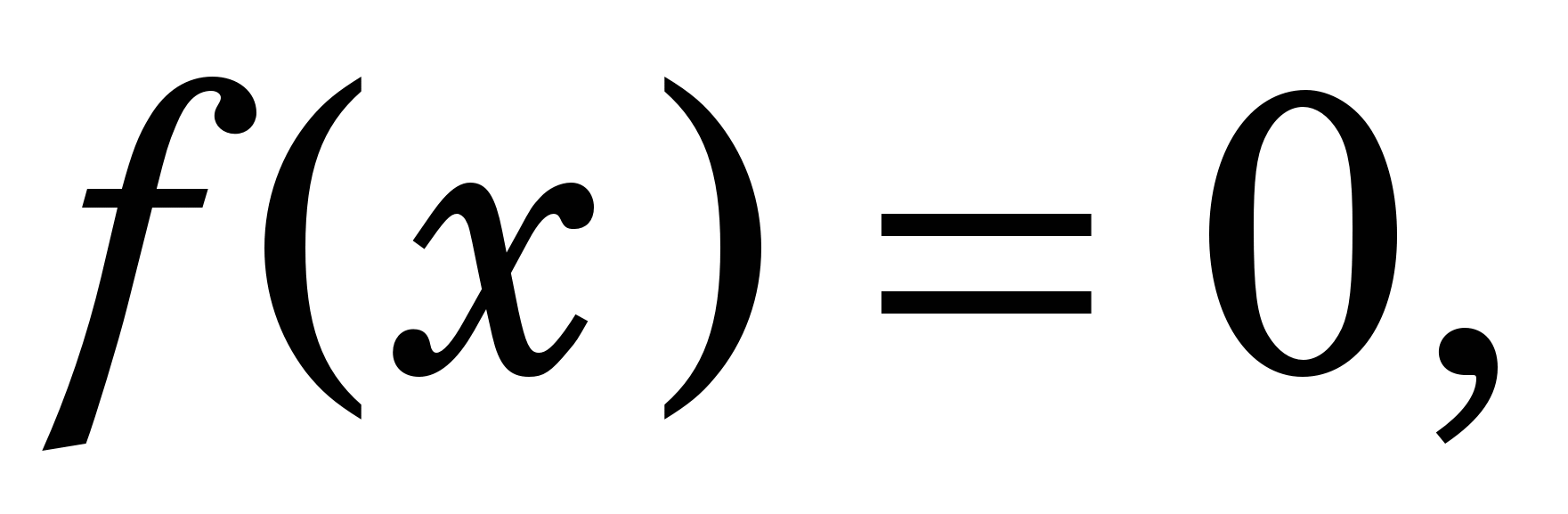 (3.7) (3.7)
де 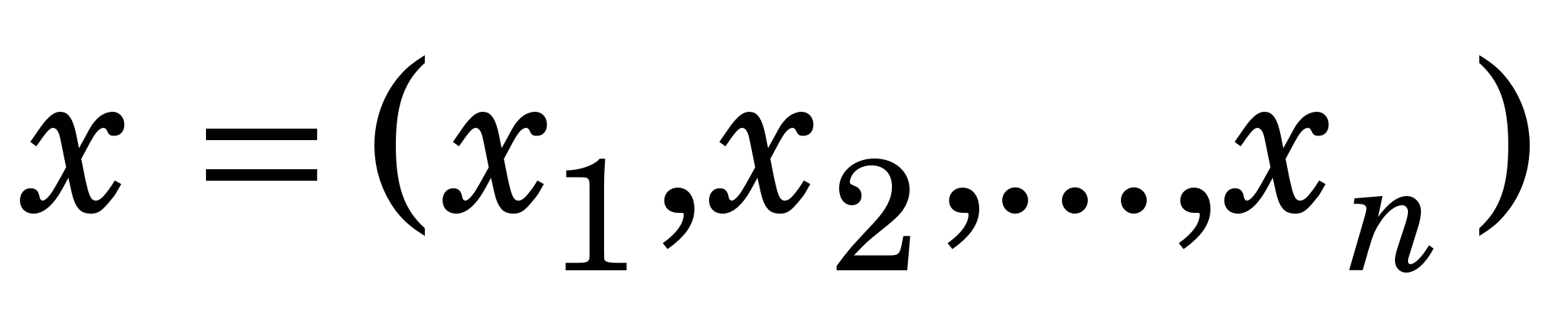 і і 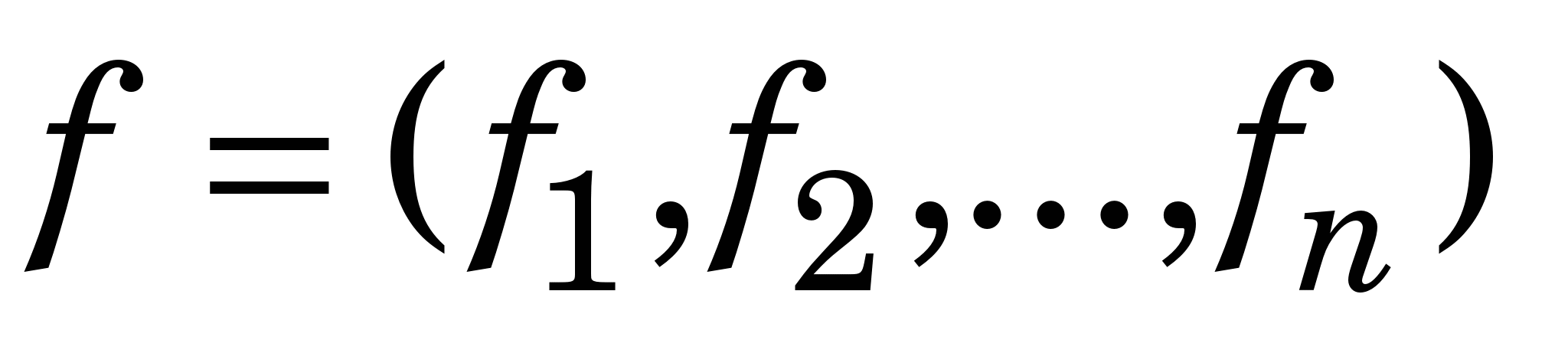 . .
Розв’язання (3.6) — набагато складніша задача, ніж розв’язання одного рівняння. Такі системи, як правило, розв’язують лише ітераційними методами.
Якщо 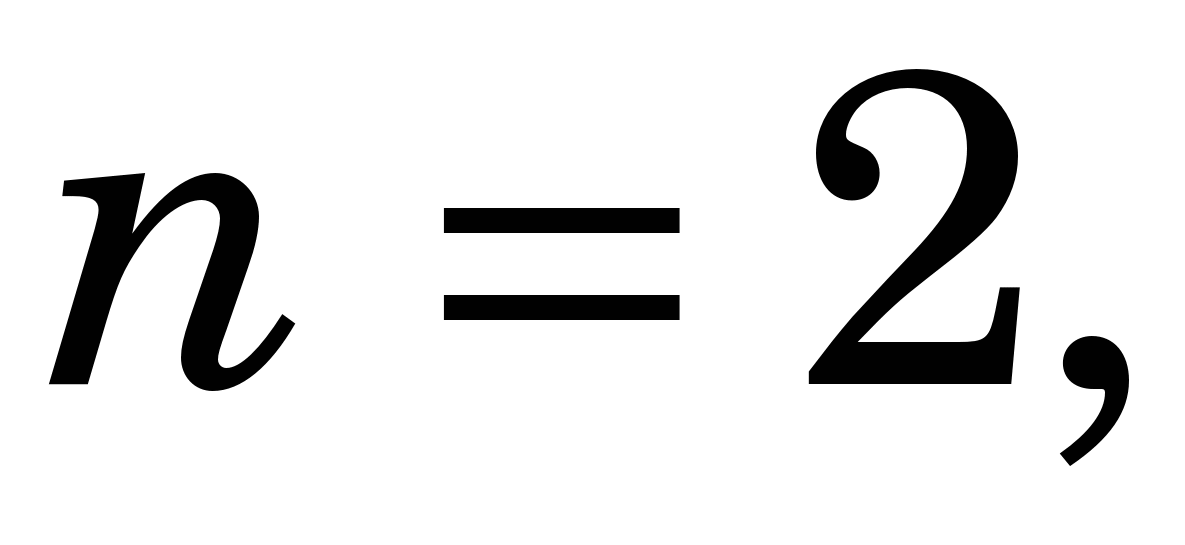 то за нульове наближення то за нульове наближення 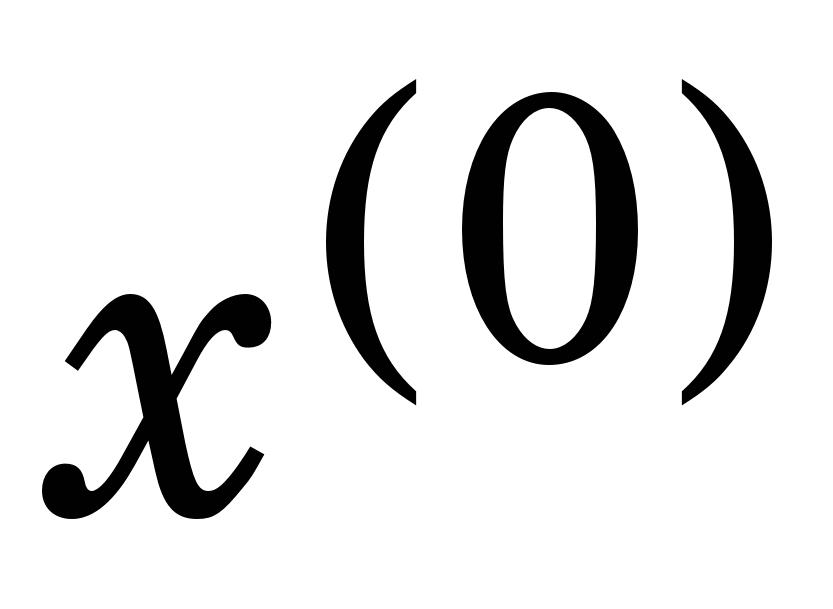 до розв’язку до розв’язку 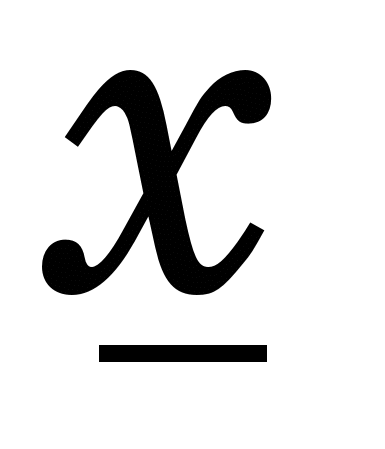 можна взяти координати точок перетину графіків можна взяти координати точок перетину графіків
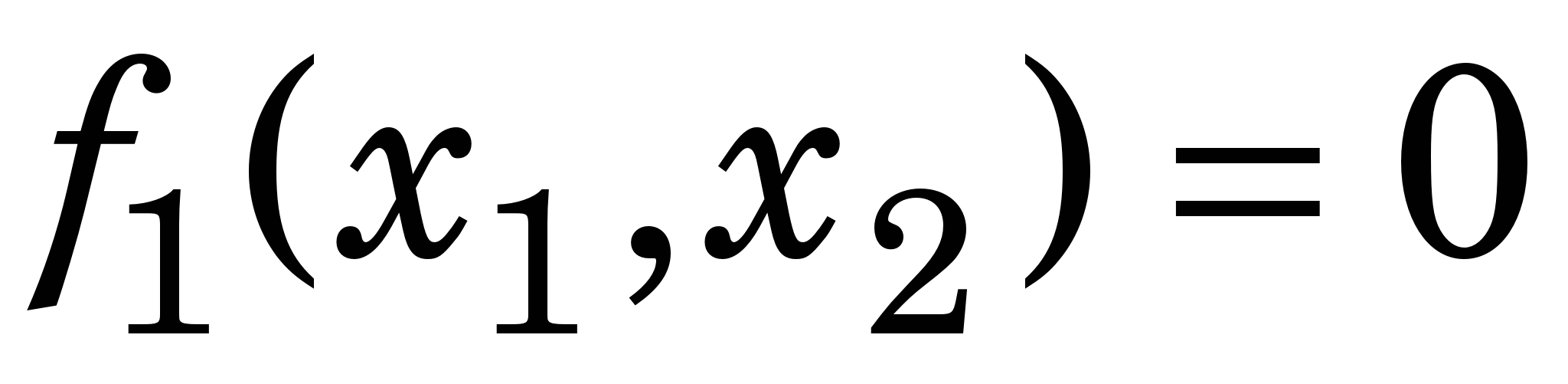 і і 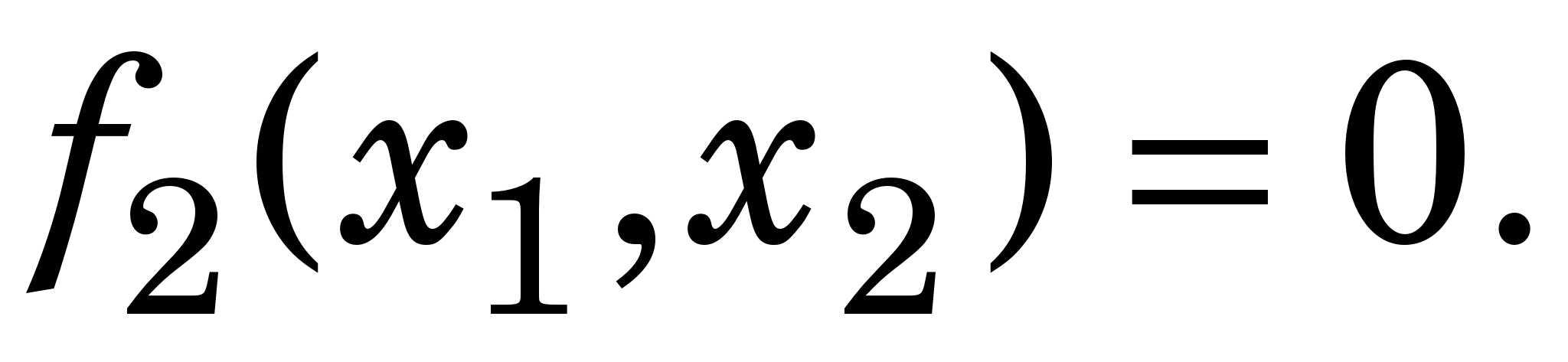
До речі, якщо 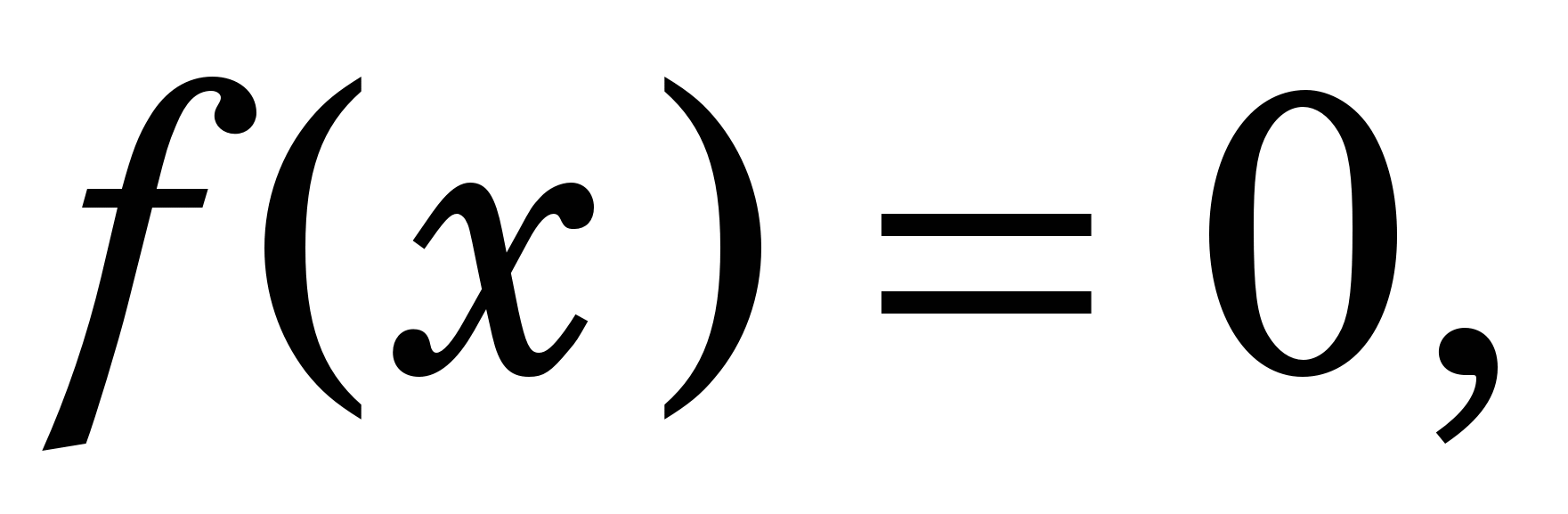 де де 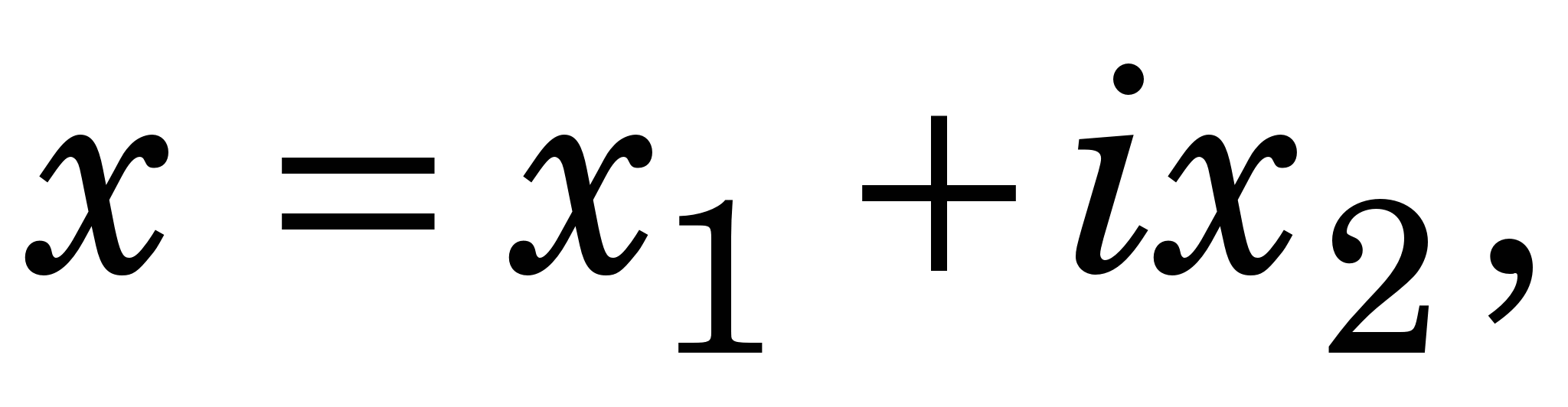 замість такого рівняння можна розглядати систему нелінійних рівнянь: замість такого рівняння можна розглядати систему нелінійних рівнянь:
 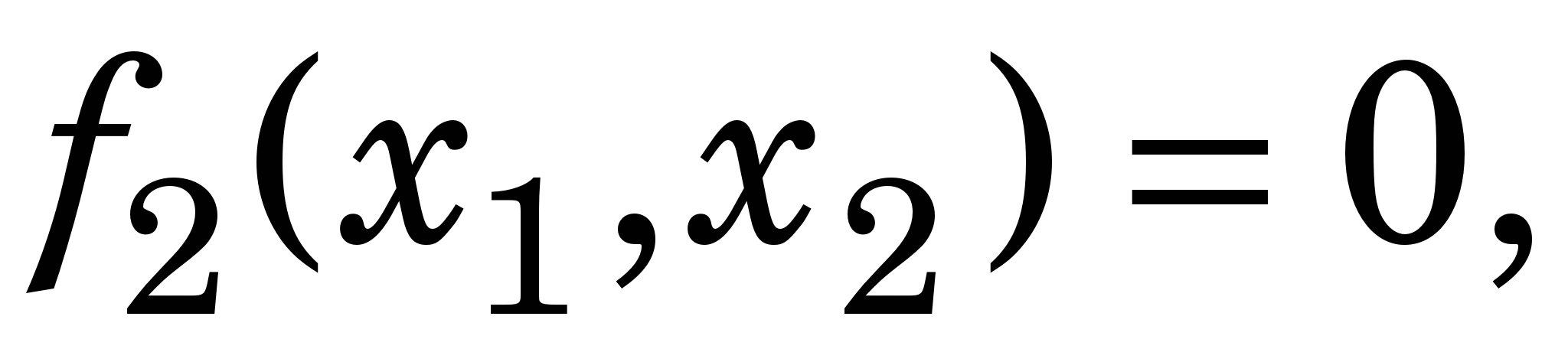 (3.8) (3.8)
де
 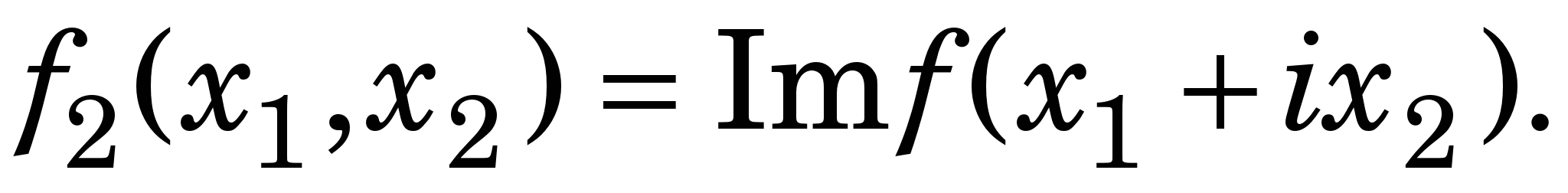
Для трьох і більше невідомих задовільних способів знаходження нульових наближень немає, але іноді 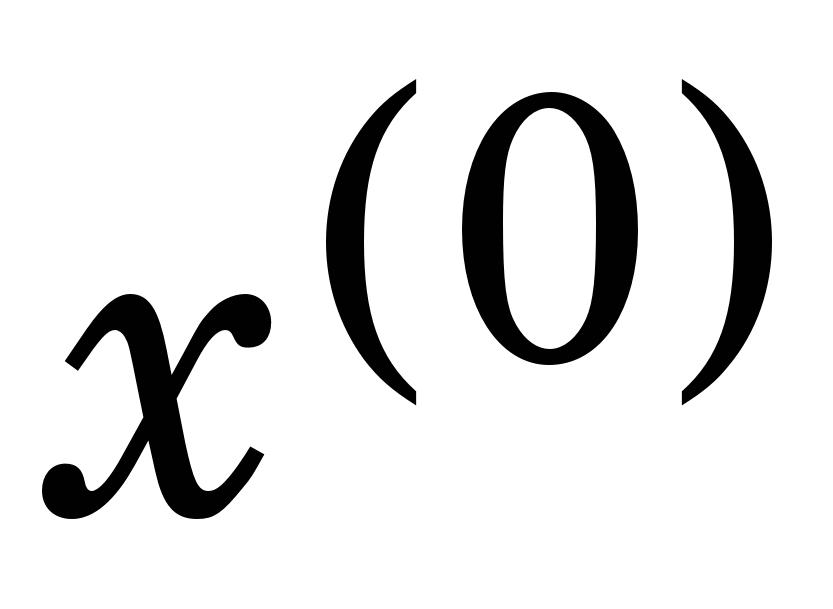 можна вибрати, виходячи з фізичних міркувань або аналізу задачі. можна вибрати, виходячи з фізичних міркувань або аналізу задачі.
Удаючись до методу Ньютона (МН) знаходження розв’язку (3.6), якщо відомий будь-який наближений розв’язок 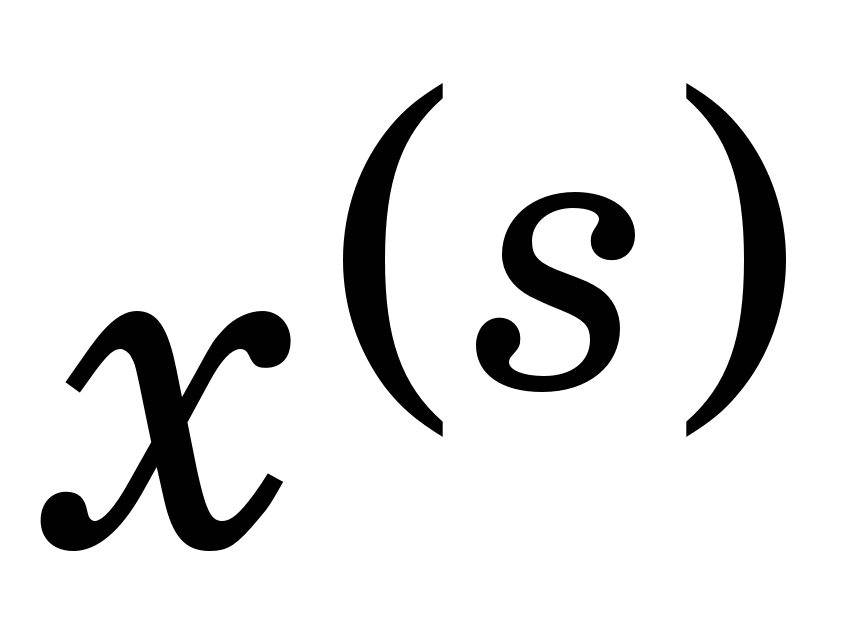 до до 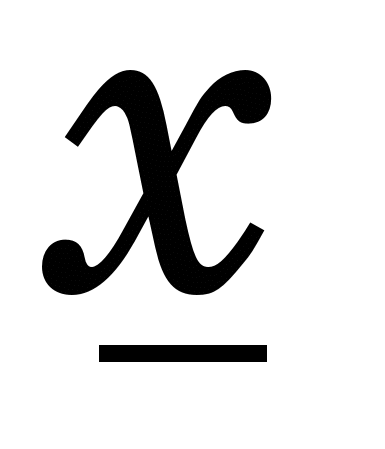 , здійснюють розв’язанням методом Гаусса такої СЛАР відносно приростів , здійснюють розв’язанням методом Гаусса такої СЛАР відносно приростів 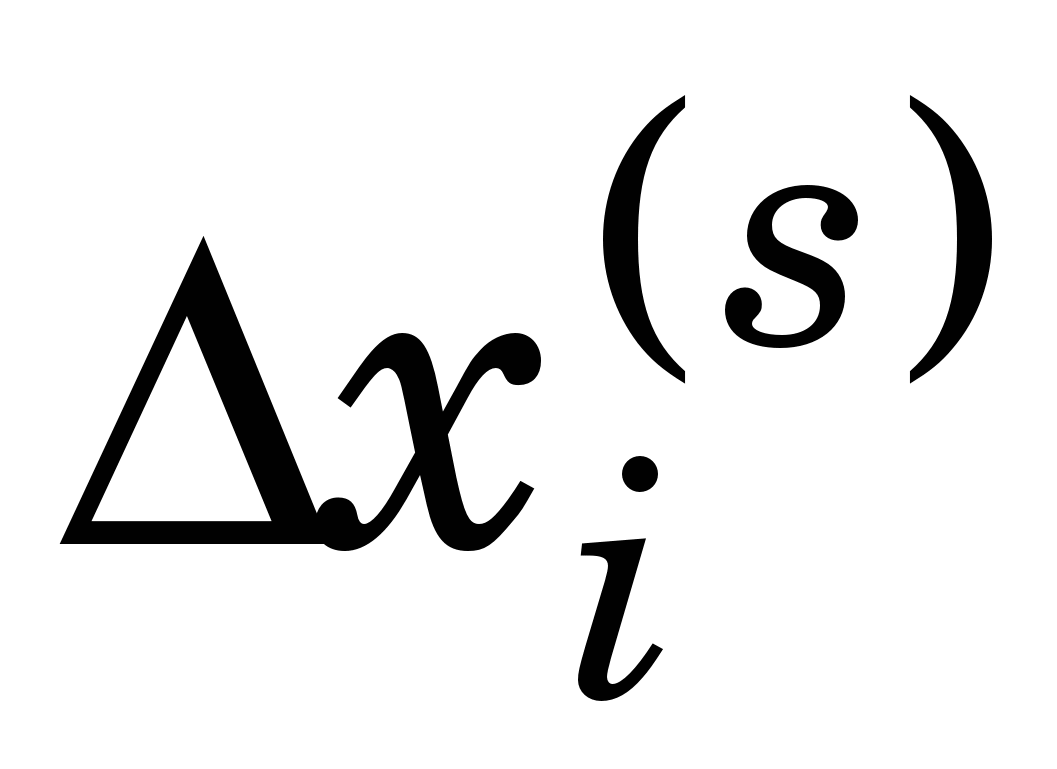 : :
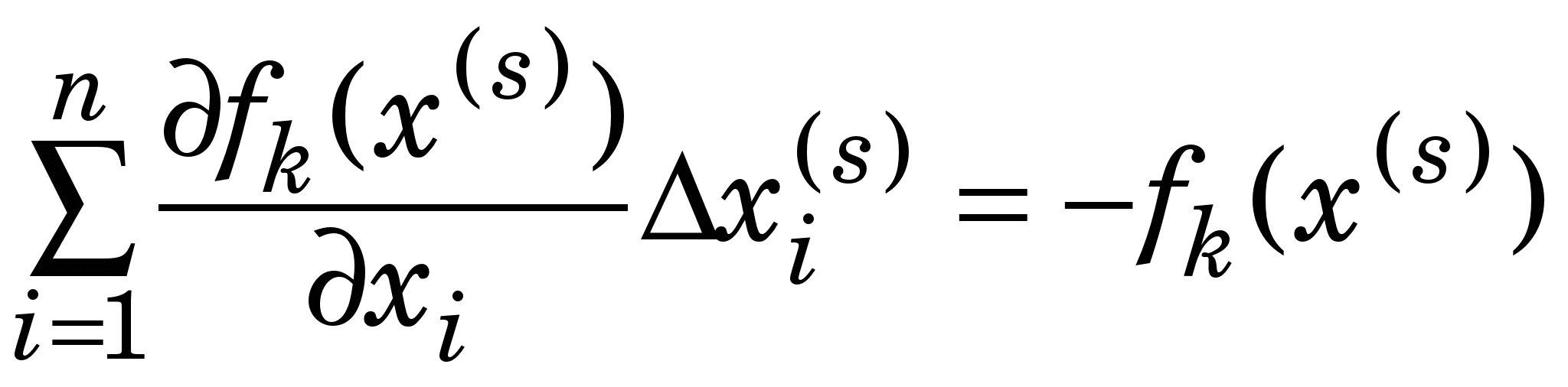  (3.9) (3.9)
Тут 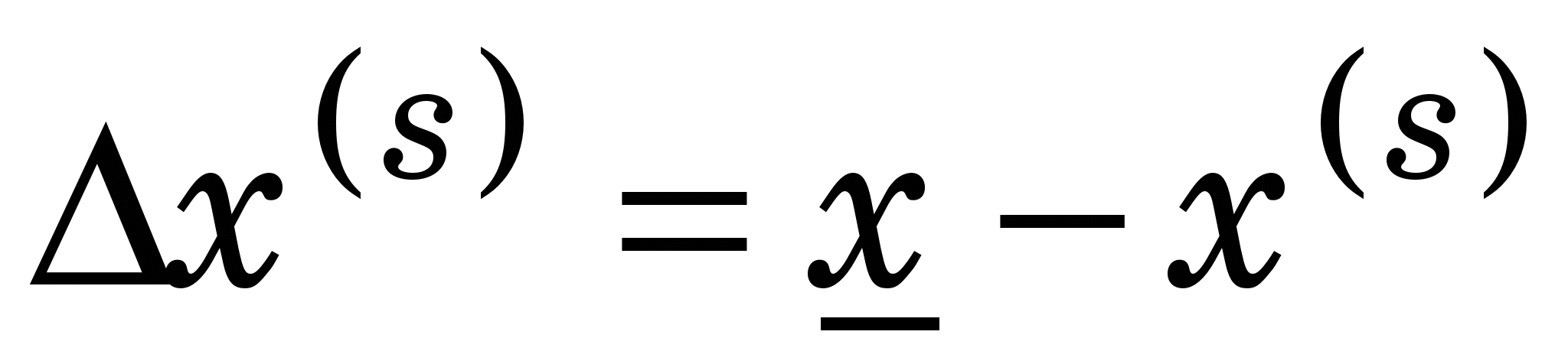 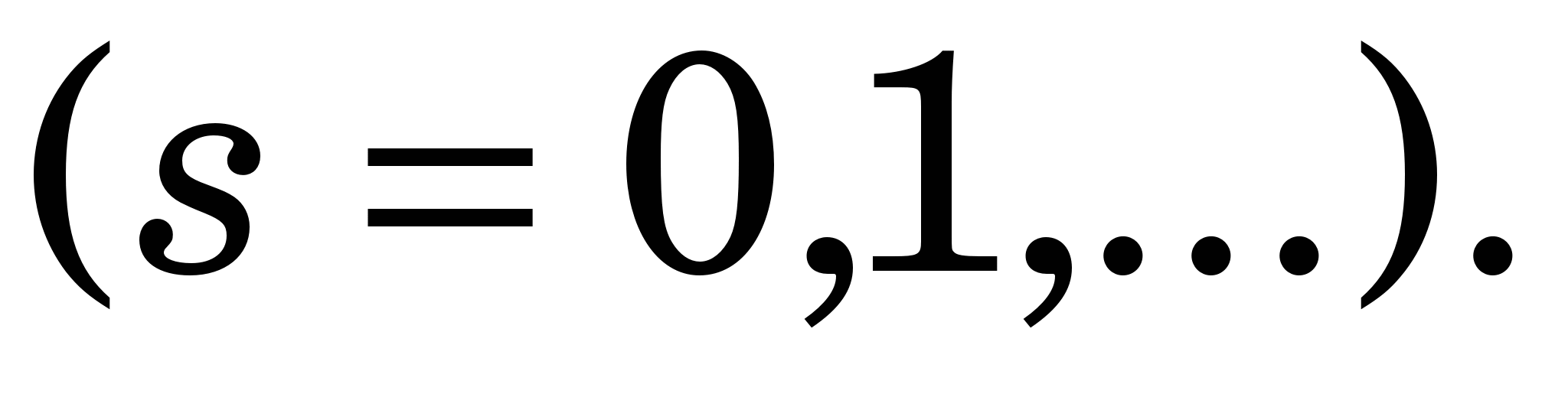
Розв’язавши СЛАР методом Гаусса (МГ), знайдемо наступні наближення:
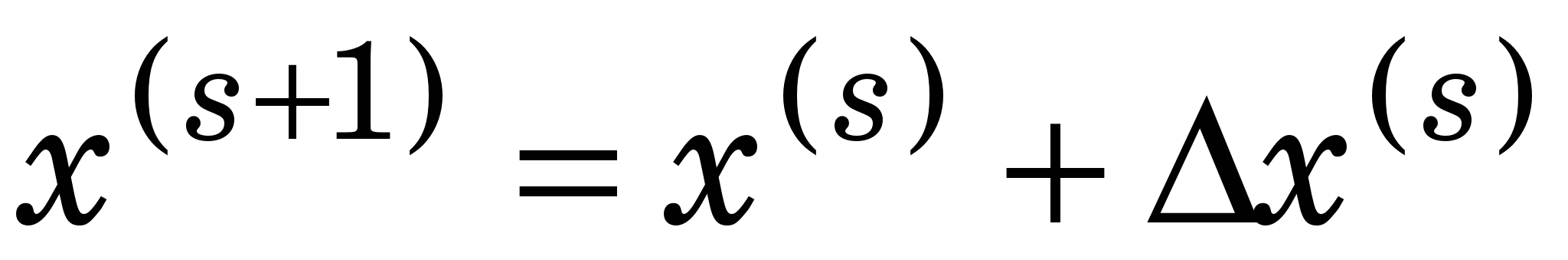 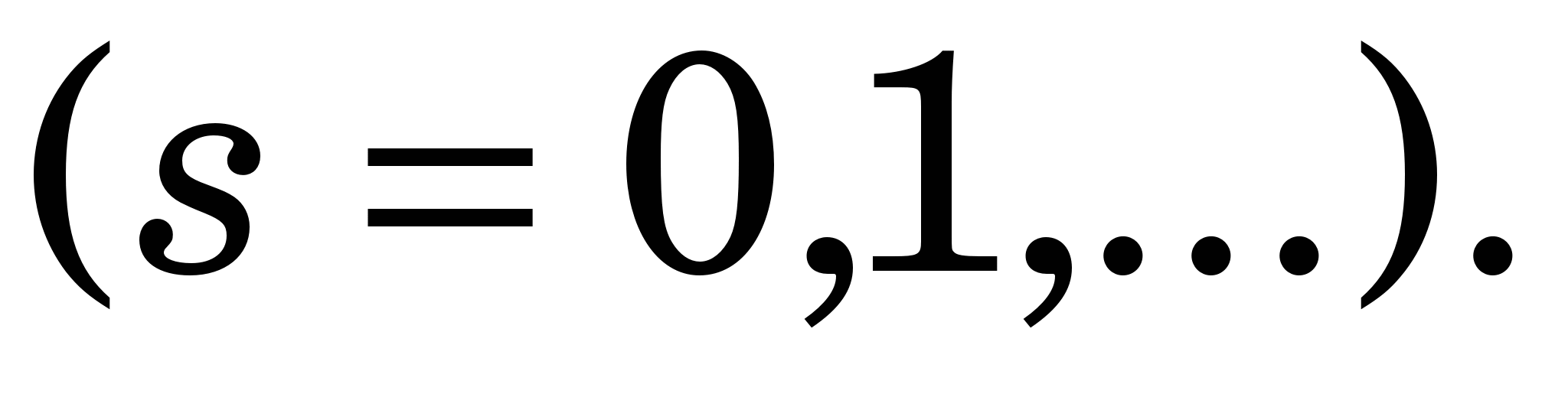 (3.10) (3.10)
За вдалого вибору 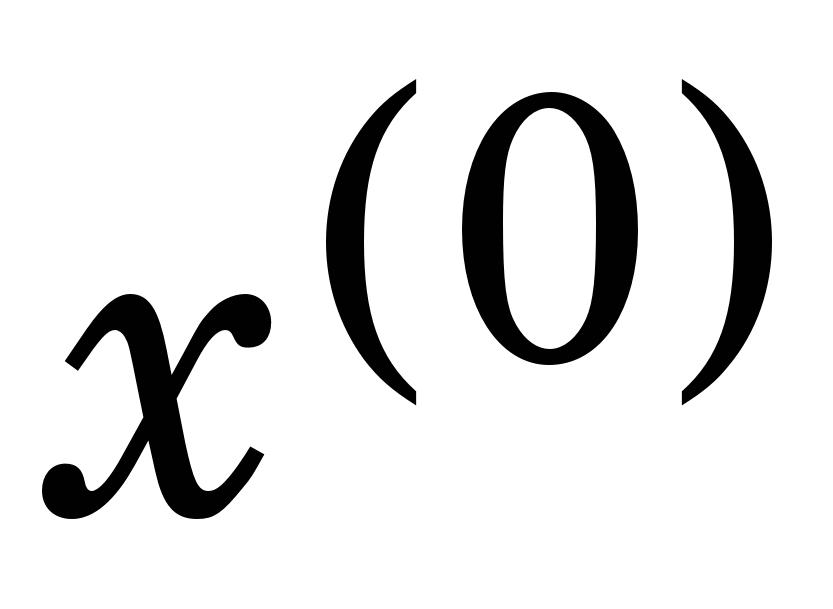 розрахунки за методом Ньютона збігатимуться, і досить швидко (3 – 5 ітерацій). розрахунки за методом Ньютона збігатимуться, і досить швидко (3 – 5 ітерацій).
На практиці ітерації припиняють за виконання умови
 (3.11) (3.11)
Приклад 3.2. Знайдемо методом Ньютона наближене значення розв’язку СНР
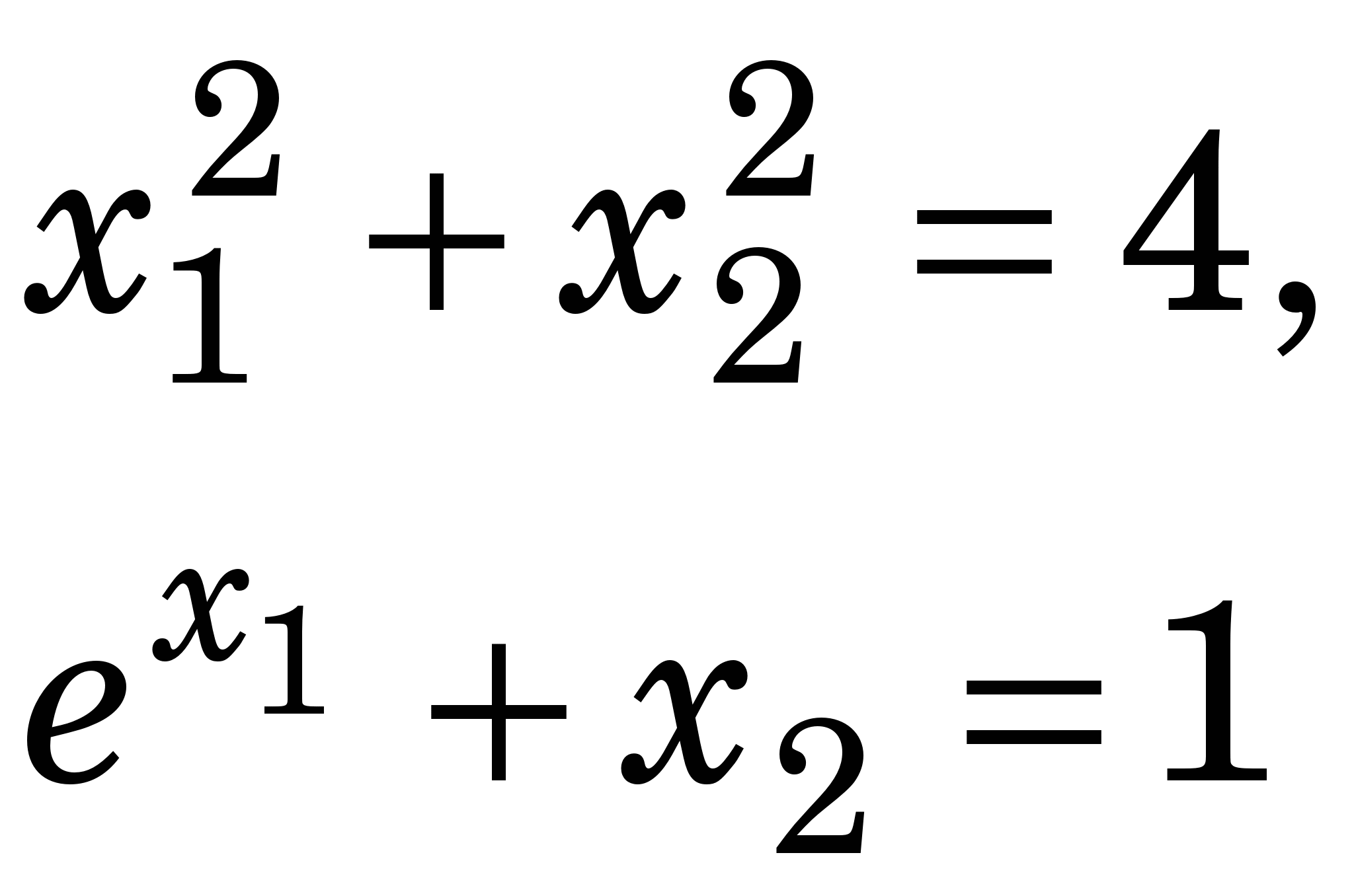
за початкового наближення  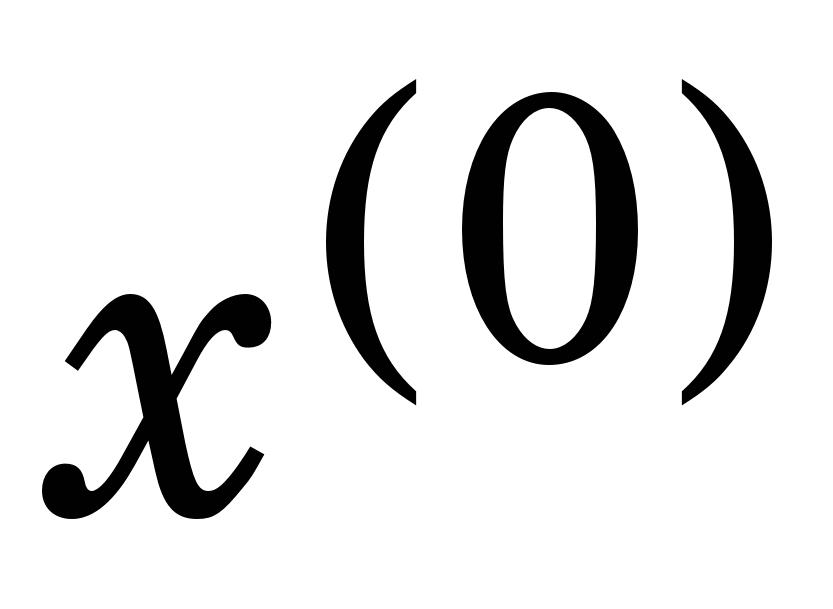 =(1.5, -1.5), яке є точкою перетину графіків =(1.5, -1.5), яке є точкою перетину графіків 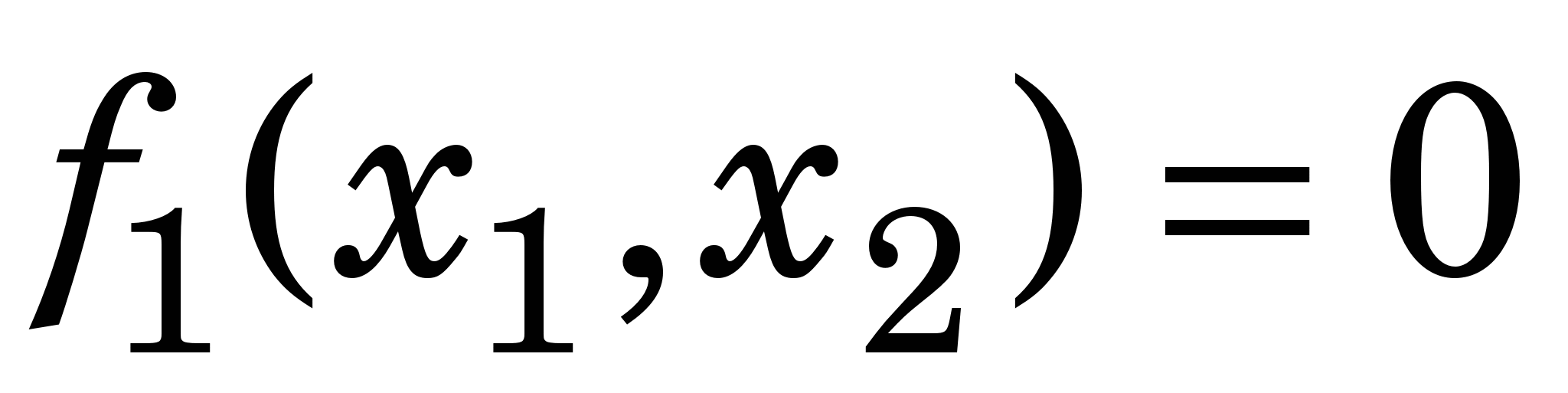 і і 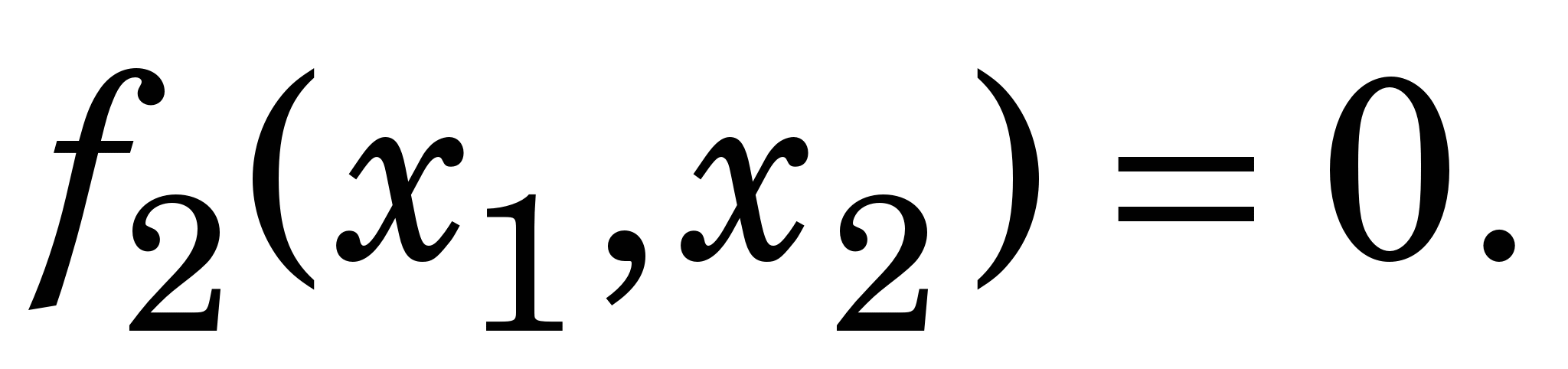
Лістинг 3.2. Файл newton:
// newton
// Розв’язання СНР (3.7) методом Ньютона (3.9)
function [s , x1] = newton(x, eps , smax);
// x – нульове наближення, eps – точність визначення
// кореня, smax – допустиме число ітерацій.
// s – число виконаних ітерацій, x1 – розв’язок (3.6)
s=0;
while (s<=smax) then
s=s+1;
// Звернення до sfdf для обчислення складових СНР (3.9)
[ff ,dd] = sfdf(x);
//Модифікація ПЧ СНР (3.9)
ff(1)=-ff(1);
ff(2)=-ff(2);
// Розв’язання СЛАР (3.9) МГ на кожній ітерації
CC=rref([dd ff]); [NN,MM]=size(CC); dx =CC(:,MM);
// Уточнення розв’язку за (3.10)
x(1)=x(1)+dx(1);
x(2)=x(2)+dx(2);
// Перевірка виконання умови (3.11)
if(sqrt((dx(1)^2+dx(2)^2)/2)<=eps) then
break;
end
end;
x1=x
endfunction;
// Функція sfdf формування складових СНР (3.9)
function [ff ,dd] = sfdf(x);
x1=x(1); x2=x(2);
// Обчислення матриці СНР (3.9)
dd (1,1) = x1*2; dd(2,1) = exp(x1);
dd (1,2) = x2*2; dd(2,2) = 1;
// Обчислення ПЧ СНР (3.9)
ff(1)=x1*x1+x2*x2-4; ff(2)=exp(x1)+x2-1;
endfunction;
//main program
// Коментар до фактичних параметрів функції newton
//[s , x1] = newton( x, eps , smax)
[s , x1] = newton([1.5 -1.5], 0.001 , 9)
Результати виконання newton
X1(1) = 1.0041687 x1(2) = - 1.7296373 s = 4.
Список рекомендованої літератури
Мусіяка, В.Г. Основи чисельних методів [Текст]: Підручник /В.Г. Мусіяка — К.: Вища освіта, 2004. — 240 с.
Поршнев, С.В. Вычислительная математика[Текст]: Курс лекцій /С.В. Поршнев. — СПб.: БХВ — Петербург, 2004. — 320 с.
Алексеев, Е.Р. Scilab: Решение инженерных и математических задач [Текст]: пособие /Е.Р. Алексеев, О.В. Чеснокова, Е.А.Рудченко. — М.: ALT Linux; Бином. Лаборатория знаний, 2008. – 260 с.
http://window.edu.ru/window/library/pdf2txt?p_id=28168
Павлова, М.И. Руководство по работе с пакетом Scilab [Текст] /М.И. Павлова. — http://www.csa.ru/
zebra/my_scilab/
Тропин, И.С. Численные и технические расчеты в среде Scilab (ПО для решения задач численных и технических вычислений) [Текст]: Учеб. пособие /И.С. Тропин, О.И. Михайлова, А.В. Михайлов. — М.: 2008. — 65 с.
Baudin, М. Введение в Scilab [Текст]/ М. Baudin; перевод с англ.:А. Glebov. 2010 г.
http://forge.scilab.org/upload/docintrotoscilab/files/introscilab-v1.3-ru.pdf .
http://www.scilab.org.Exec-файл scilab-5.2.2.exe.
Додатки
Додаток 1
Основні елементи мови пакета Scilab
Пакет Scilab – діалогова система, яка дозволяє вводити команди й відстежувати результати їх виконання. Після пуску пакета Scilab в OS Windows за допомогою scilab-5.2.2.exe на екрані дисплея з’явиться наведене нижче командне вікно (консоль):
___________________________________________
scilab-5.2.2
Консорціум Scilab (DIGITEO)
Авторські права належать INRIA, ©1989–2010
Авторські права належать ENPC, ©1989–2007
___________________________________________
Команда запуску:
завантаження початкового середовища
-->
Символ --> є запрошення до введення команд. Після цього символу вводять команду або програму. Їх введення завершується натисненням на клавішу <Enter>.
Прикладом найпростішої програми мовою Scilab є програма gauss, яка реалізує метод Гаусса під час розв’язання СЛАР:
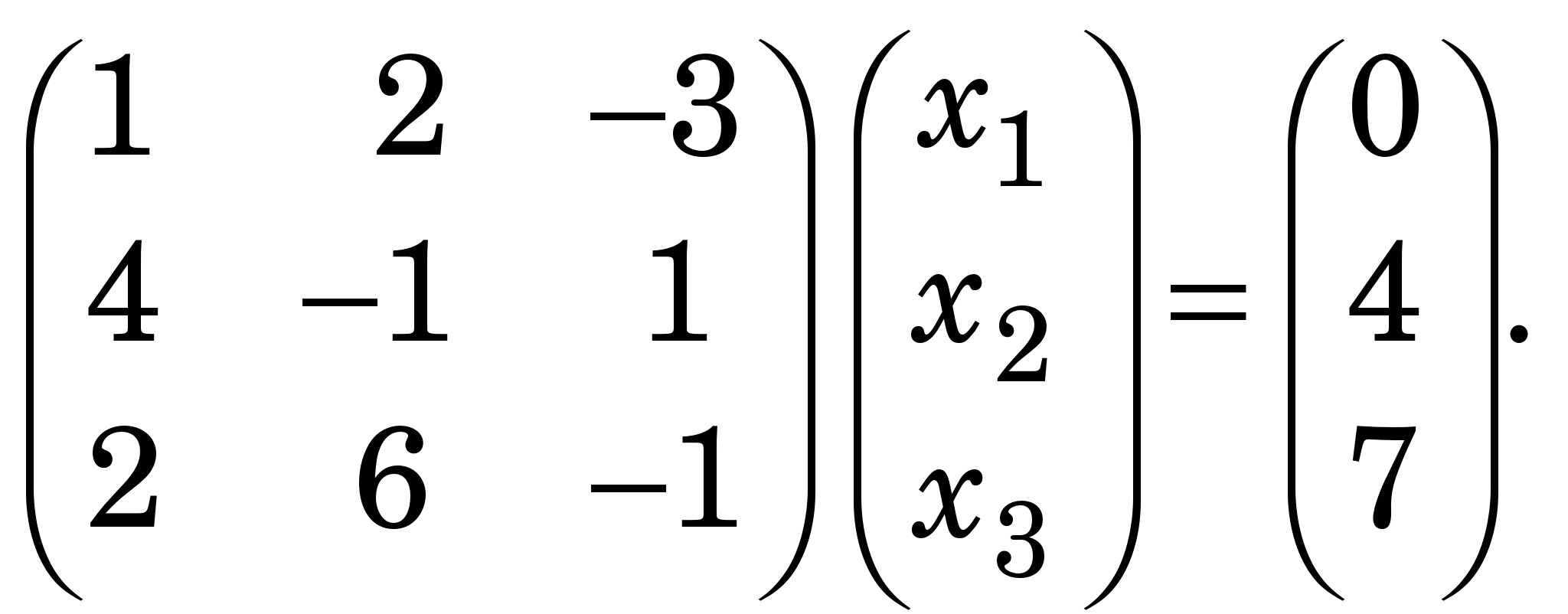
// gauss
A=[1 2 -3; 4 -1 1; 2 6 -1]; b=[ 0; 4; 7];
C=rref([A b]); [NN,MM]=size(C); x=C(:,MM); x=x.'
Результат виконання програми gauss: x = 1. 1. 1.
Перший рядок – коментар, другий – формування матриціA та вектора b СЛАР. Перші три команди 3-го рядка саме й реалізують метод Гаусса розв’язання СЛАР, а 4-й – транспонує матрицю стовпчик (вектор) на матрицю-рядок для його друку у вигляді рядка.
Якщо команда завершується крапкою з комою (;), то результат роботи команди не виводиться на консоль, у іншому ж випадку результат виводиться. Довгі командні рядки можна розбивати на два, додаючи в місці розбиття три крапки (…).
Математичні вирази, як і знаки дій, записують подібно до інших мов програмування.
Як і в інших мовах програмування, об’єктами Scilab є скалярні величини, вектори (одновимірні масиви) та матриці (багатовимірні масиви).
Визначені в Scilab стандартні скалярні величини починаються з % (%pi - число π, %e – число e=2.71828 …).
Порядок формування матриць і векторів у Scilab показано на прикладі програми gauss. Індекси елементів векторів та матриць починаються з одиниці. Імена змінних завжди починаються з букв.
У пакеті Scilab є вбудовані функції (sin(x), cos(x), …), а втім того їх можуть будувати і користувачі двома способами:
deff('f = ff(x)','f = log(1+x)'); y=ff(2)
або
function [f] =ff(x);
f = log(1+x)
endfunction; y=ff(2)
Результат виконання обох програм однаковий: y = 1.0986123 .
У пакеті Scilab прийнята загальновідома конструкція циклу. Цикл, як і умовний оператор, завершується командою еnd, наприклад:
for n=n1:step:n2
// n - змінна циклу, n1 і n2 початкове і кінцеве значення змінної циклу n,
// step - крок змінювання i (якщо крок циклу step=1, його можна опускати)
a=n*n; // тіло цикла
еnd
Приклад циклу while
x=0;
while x<10
x=x^2+1
end
Виконання циклів while і for можна перервати командою break, наприклад,
for i=1:n
if(xj>=xx(i)&xj
k=i;
break;
end
end;
Застосування команди plot для побудови графіка показано у процесі розв’язання задачі коливання математичного маятника у пакеті Scilab
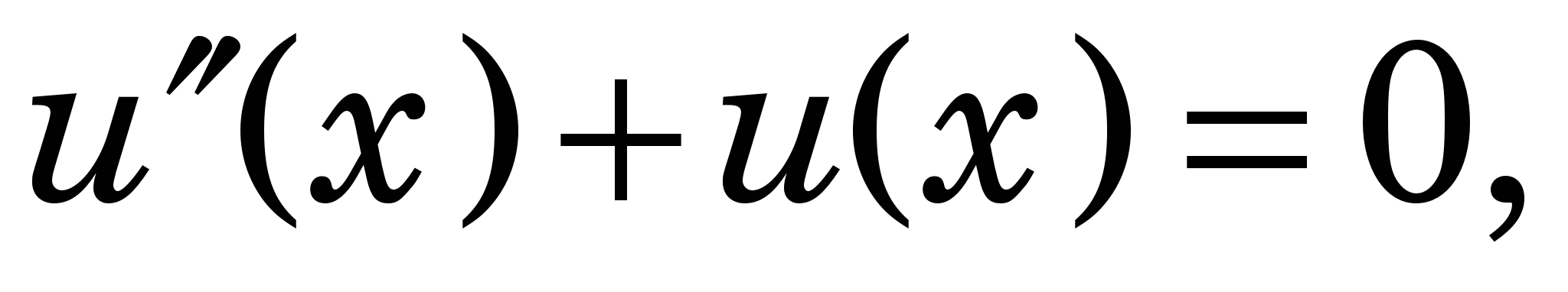  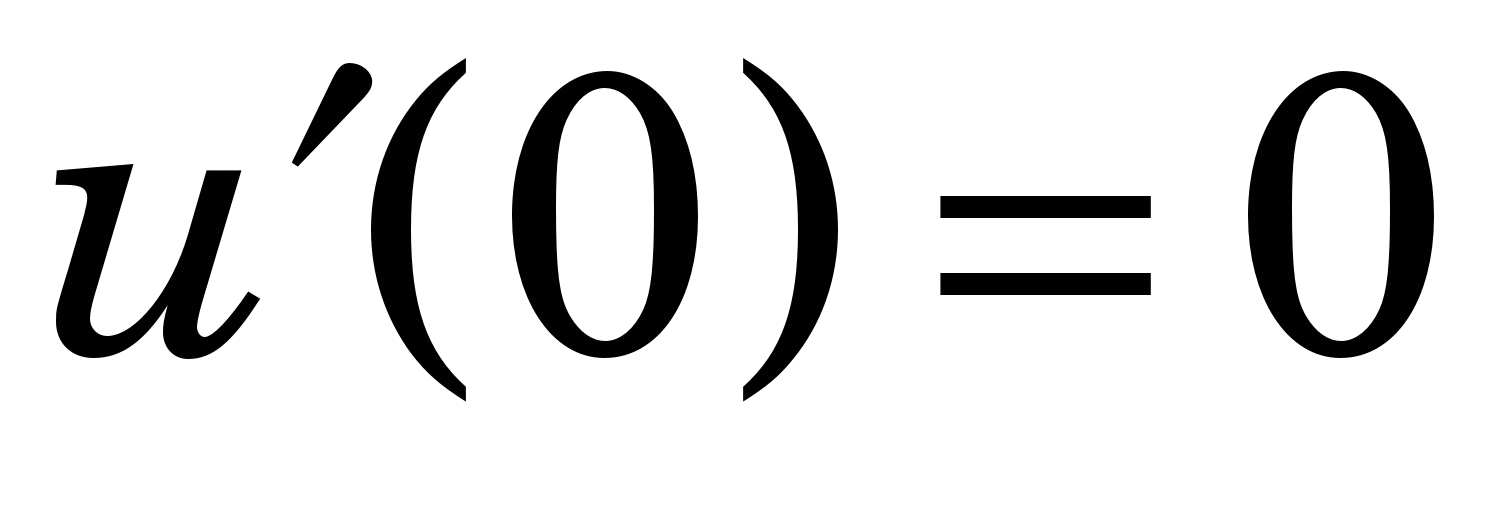
function dy = syst(t,y)
dy=zeros(2,1); dy(1) = y(2); dy(2) = - y(1);
endfunction;
x0=[2;0];t0=0;t=0:0.5:2;
y=ode(x0,t0,t,syst)
plot(t,y); xgrid();
y =
2. 1.7551653 1.0806047 0.1414745 - 0.8322937
0. - 0.9588513 - 1.6829421 - 1.9949901 - 1.818595
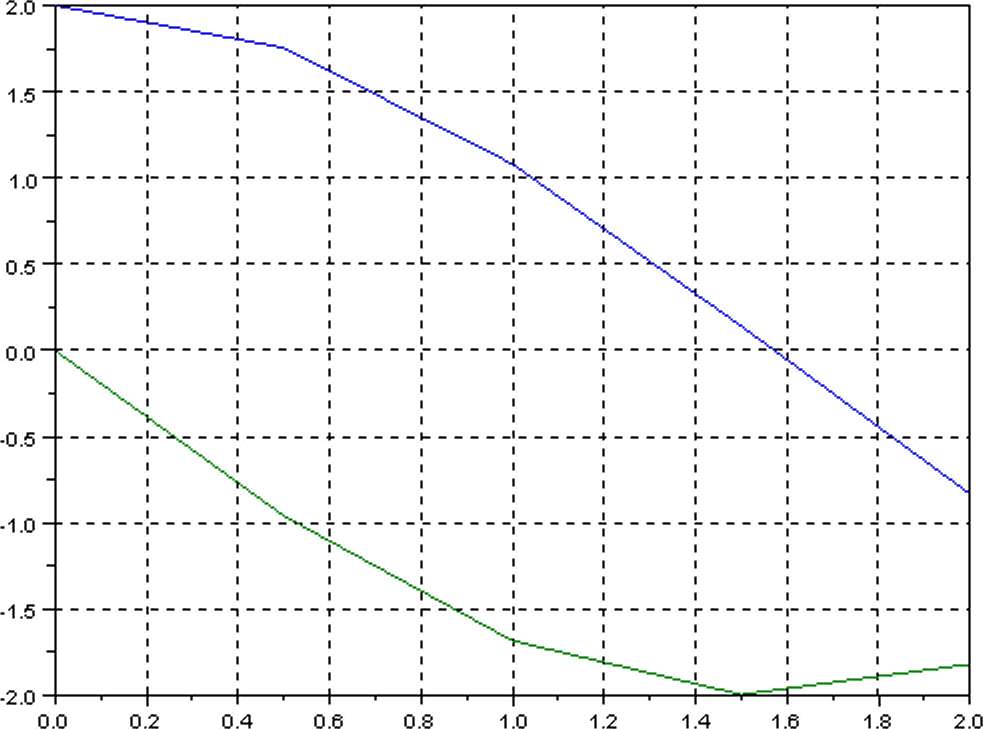
На графіку верхня крива – розв’язок u(x), а нижня крива – похідна від нього
Додаток 2
Завдання для лабораторних робіт із застосуванням числових методів розв’язання задач
Вихідні дані для всіх завдань слід брати із відповідних таблиць згідно з одержаним шифром. Наприклад, якщо шифр 27964, то дані 1-го стовпчика необхідно брати з 2-го рядка, дані 2-го стовпчика – з 7-го рядка й т.д. Якщо у відповідній таблиці стовпчиків більше ніж 5, то потрібно взяти необхідну кількість перших цифр із шифру і доповнити ними заданий шифр. Наприклад, якщо у таблиці 8 стовпчиків, то новий шифр буде таким: 27964279.
Текст робіт слід набирати на комп’ютері за допомогою текстового редактора Word і роздруковувати на одному боці аркуша білого паперу формату А4 (210×297 мм), дотримуючись таких розмірів полів: верхнє, ліве і нижнє – не менше 20 мм, праве – не менше 10 мм. Розмір шрифту повинен відповідати 14 (або 12) пунктам Times New Roman, міжрядковий інтервал при цьому має бути полуторний.
Завдання 1. Інтерполяція функції поліномом Ньютона
Побудувати інтерполяційний поліном 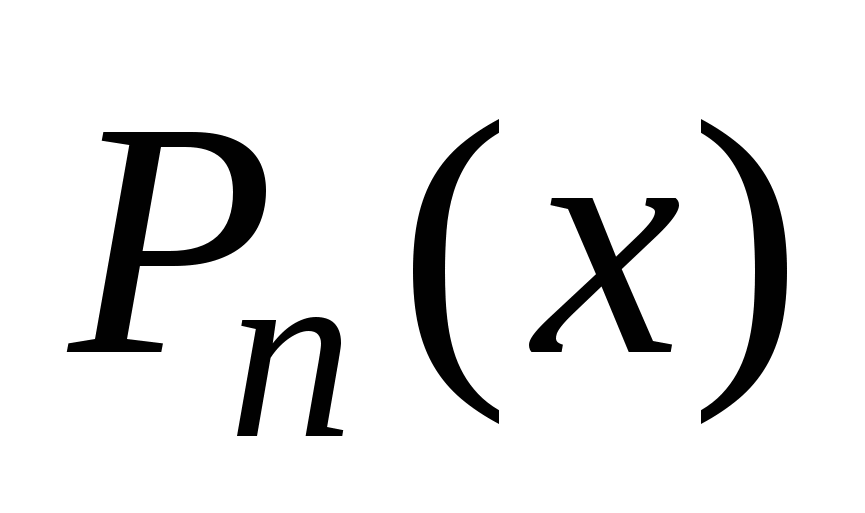 у формі Ньютона для функції у формі Ньютона для функції
y(x)= k1 f1(x) + k2 f2(x) + C
у точках 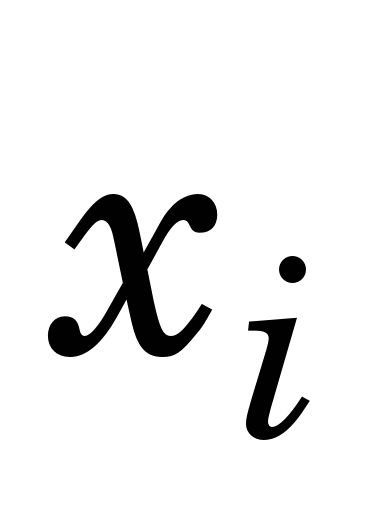 , значення яких слід шукати за співвідношеннями , значення яких слід шукати за співвідношеннями
a = 0.08 |k1|, b = 0.135 |k2|, ξ= а + k3 (b-a), 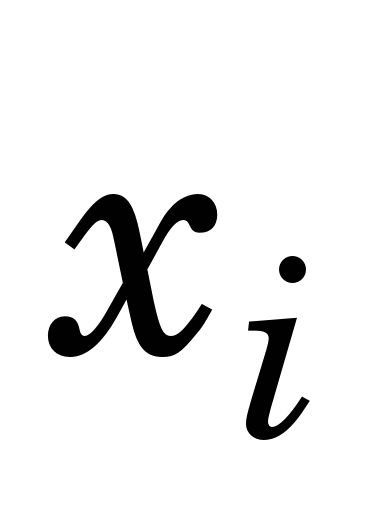 = а + i h [ = а + i h [ ; h=(b-a)/n]. ; h=(b-a)/n].
Необхідні дані взяти із табл. 1 відповідно до шифру. Значення сталої С підібрати так, щоб знак у(х) на відрізку [а,b] не змінювався й на кінцях відрізка функція не дорівнювала нулю.
Одержаний ІПН 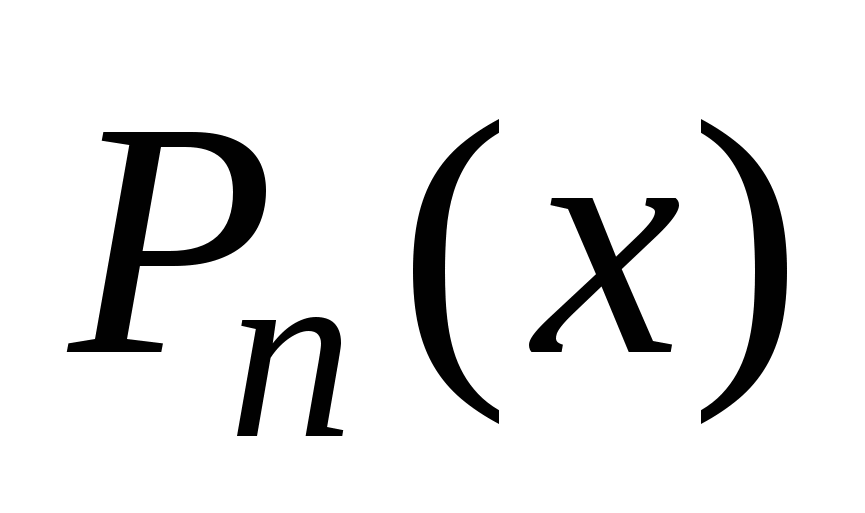 застосувати для обчислення наближених значень y(x) у М точках, зокрема, серед них повинні бути вузли інтерполяції та точка ξ, у якій до того ж необхідно обчислити значення абсолютної похибки застосувати для обчислення наближених значень y(x) у М точках, зокрема, серед них повинні бути вузли інтерполяції та точка ξ, у якій до того ж необхідно обчислити значення абсолютної похибки 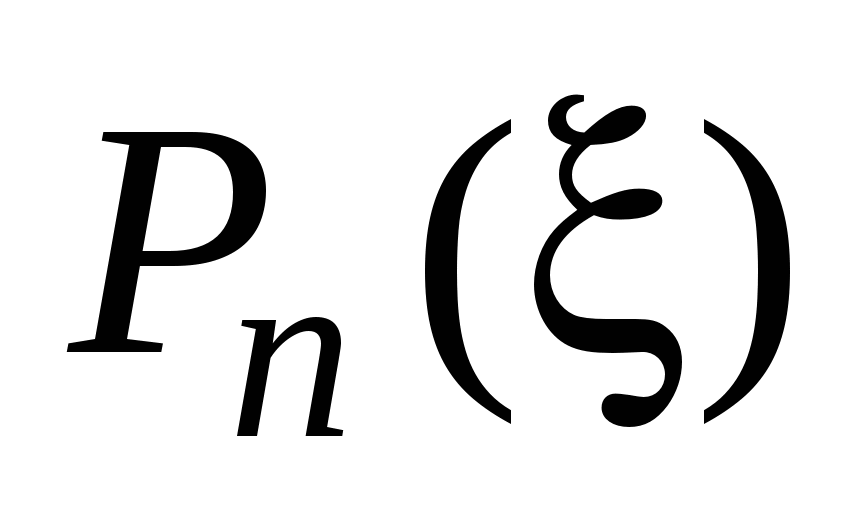 - -  та похибки інтерполяції rn (ξ). та похибки інтерполяції rn (ξ).
Побудувати графіки у(х) та 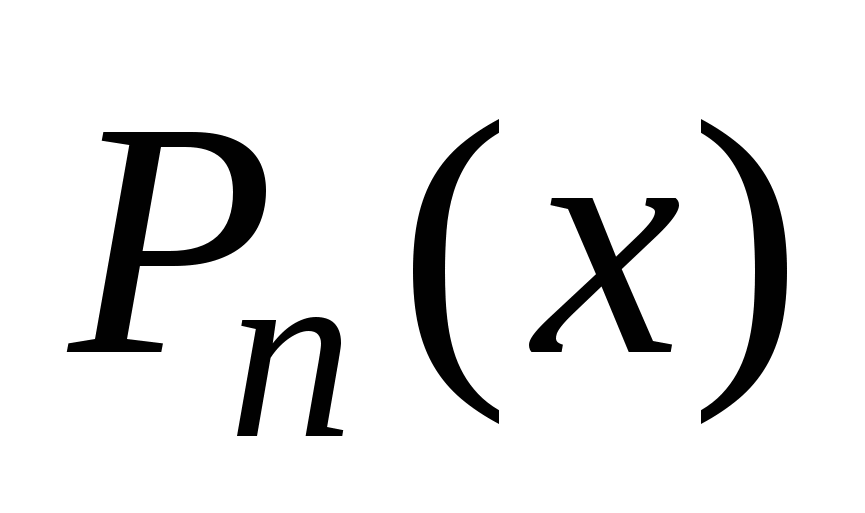 за обчисленими їх М значеннями. за обчисленими їх М значеннями.
Завдання 2. Інтерполяція функції вільними кубічними сплайнами
Побудувати вільні кубічні сплайни для функції з попереднього завдання, взявши за вузли точки 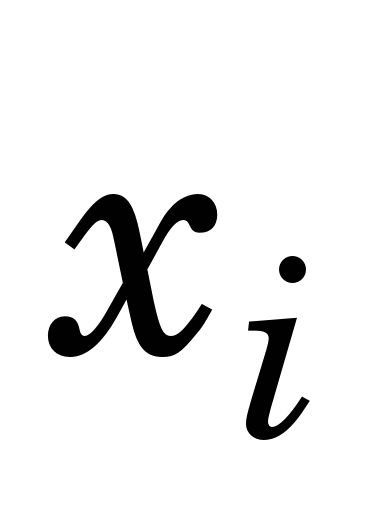 = а + i h [ = а + i h [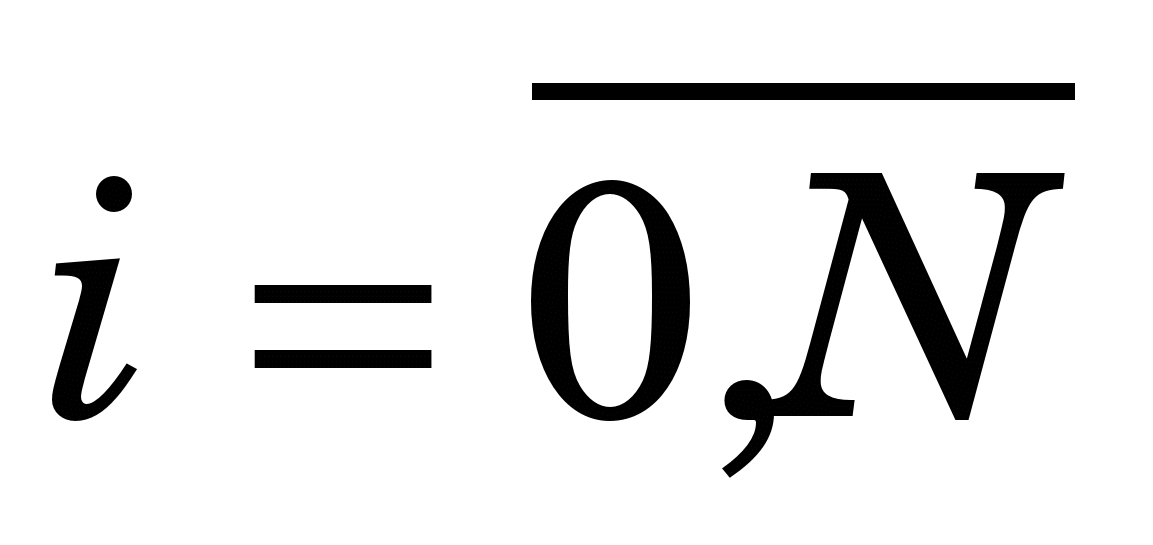 ; h=(b-a)/N],й застосувати їх для обчислення значень y(x) у тих же точках, що й у завданні 1, та побудувати за обчисленими М значеннями графіки у(х) та s(x). ; h=(b-a)/N],й застосувати їх для обчислення значень y(x) у тих же точках, що й у завданні 1, та побудувати за обчисленими М значеннями графіки у(х) та s(x).
Завдання 3. Наближення функції методом найменших квадратів
Визначити коефіцієнти алгебричного полінома
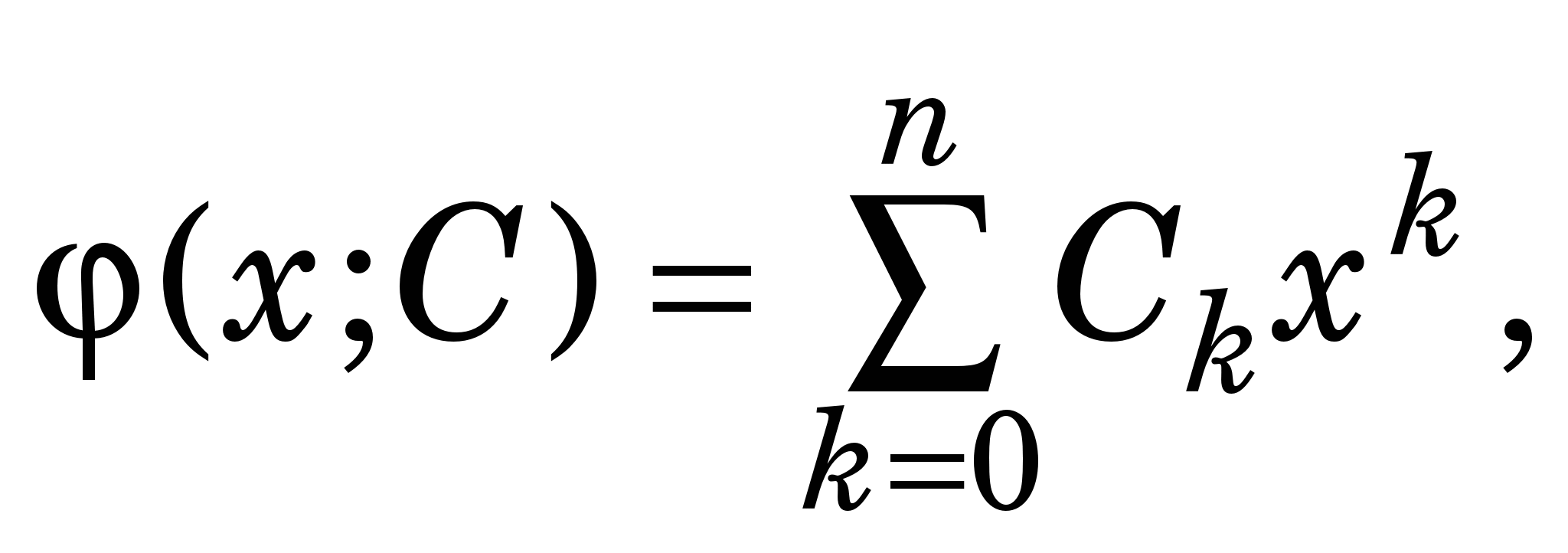
який апроксимує в середньому таблично задану функцію у(х) (із завдання 1) за знайденими її значеннями у точках 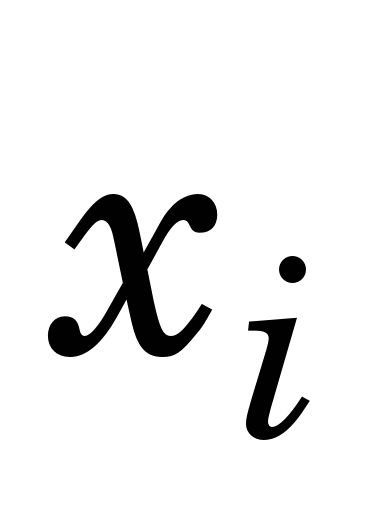 = а + (i-1)h [ = а + (i-1)h [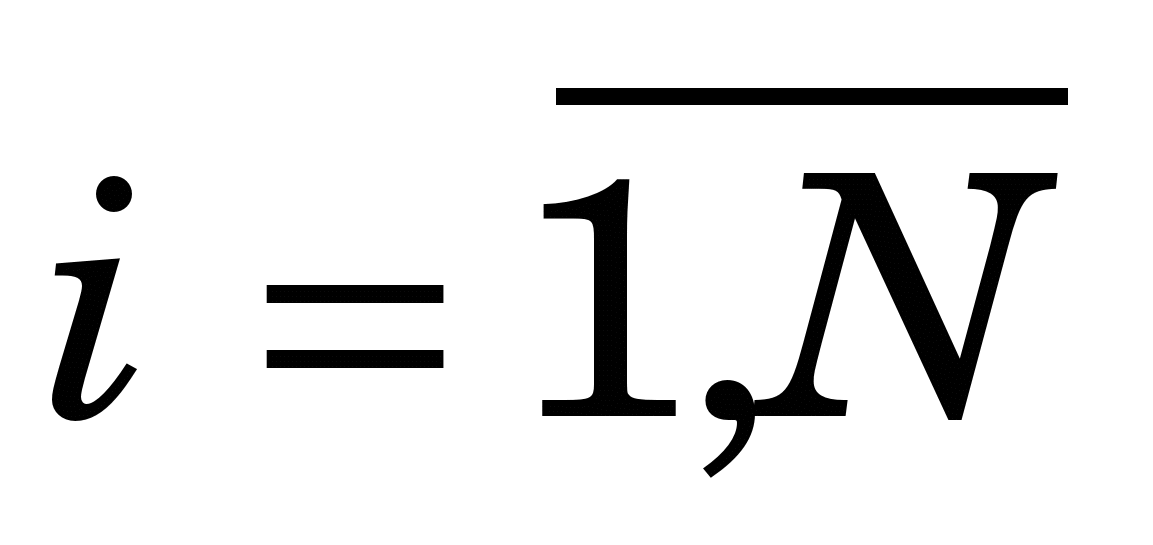 ; h=(b-a)/(N-1)] . ; h=(b-a)/(N-1)] .
Побудовану функцію φ(х) застосувати для обчислення наближених значень у(х) у тих же точках, що й у завданні 1, визначити середнє квадратичне відхилення φ(х) від у(х) та побудувати графіки функцій у(х) і φ(х).
Завдання 4. Числове інтегрування
Для заданої функції у(х) із завдання 1 обчислити значення інтеграла  , застосовуючи КФ на рівномірних сітках , застосовуючи КФ на рівномірних сітках 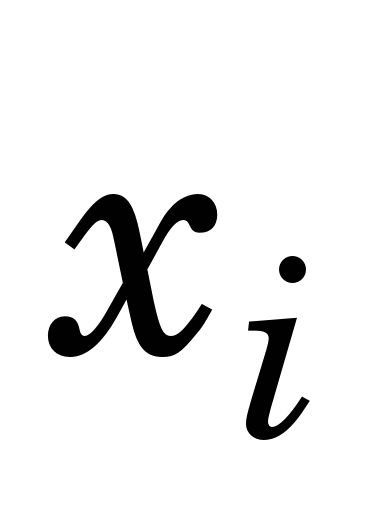 = а + i h [ = а + i h [ ; h=(b-a)/n]. ; h=(b-a)/n].
Завдання 6. Розв’язання систем нелінійних рівнянь
Застосовуючи метод Ньютона та метод простих ітерацій, визначити один із розв’язків х=(х1, х2) системи нелінійних рівнянь з точністю ε
f1(х1, х2) = 0, f2(х1, х2) = 0 . (1)
Нульове наближення розв’язку знайти графічним способом. Функції f1(х1, х2), f2(х1, х2), що входять у (1), взяти з табл. 2 відповідно до шифру. Якщо графіки функцій f1(х1, х2), f2(х1, х2) не перетинаються, то, як і в завданні 5, до однієї з них слід додати сталу D, щоб вони перетнулись.
Таблиця 1
Рядок
|
Стовпчик
|
1
|
2
|
3
|
4
|
5
|
f1(x)
|
f2(x)
|
k1
|
k2
|
k3
|
1
|
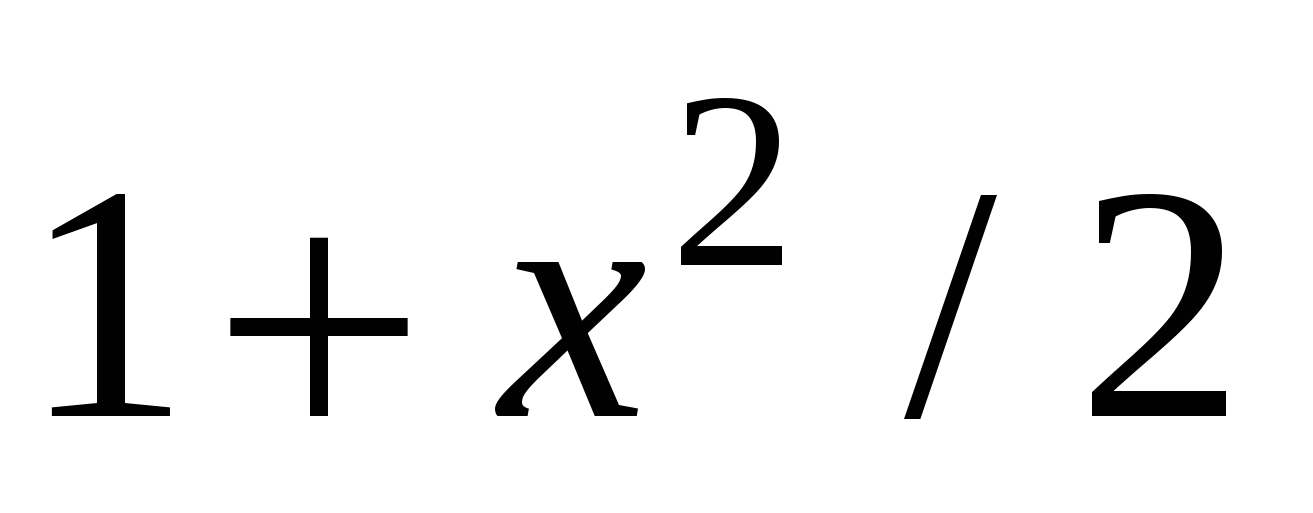
|
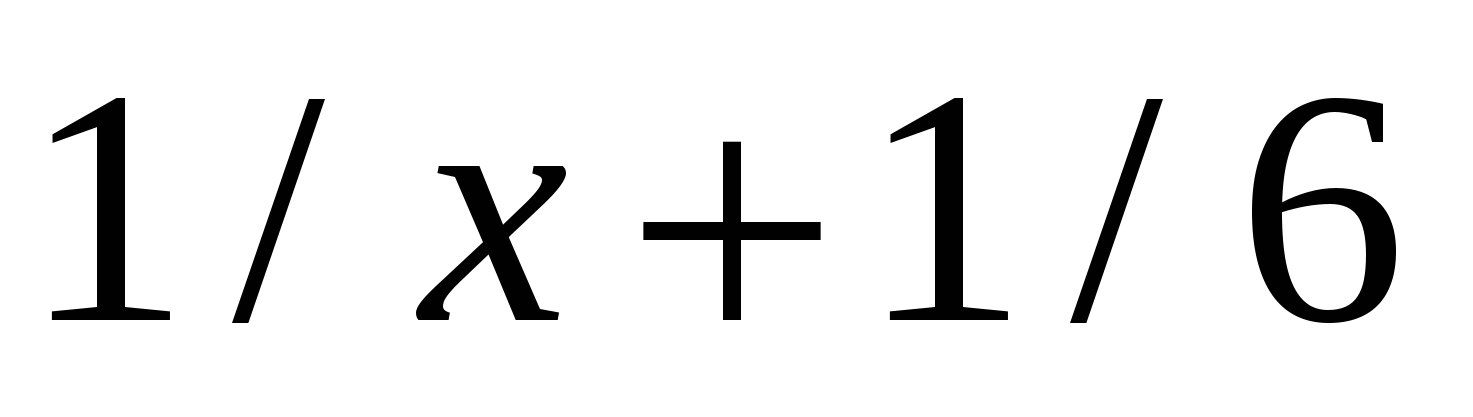
|
-1.5
|
6.5
|
1/3
|
2
|
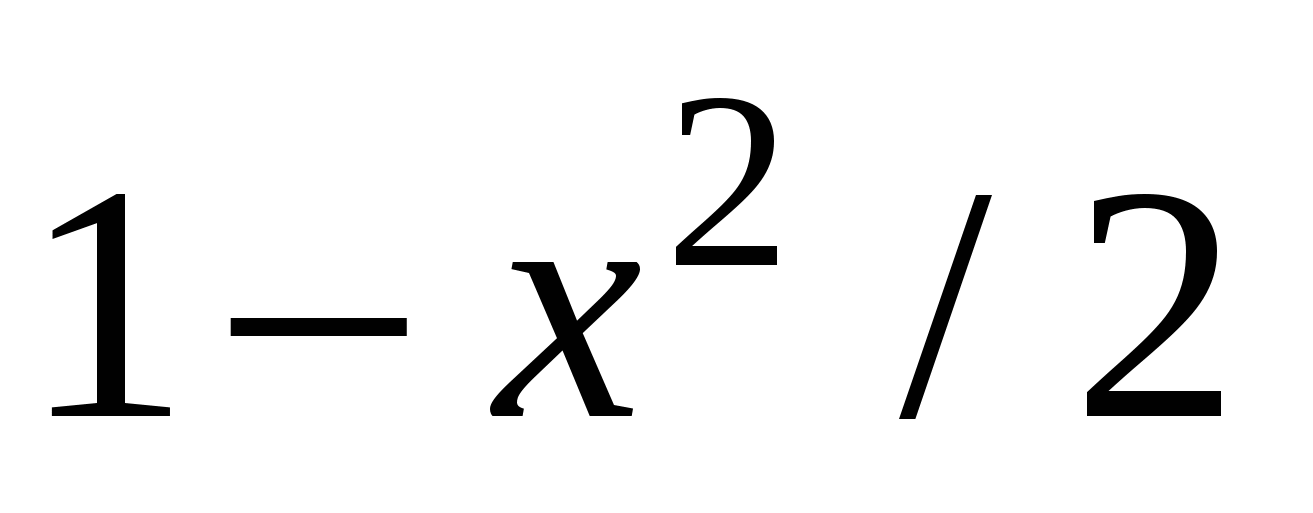
|

|
2.0
|
-7.0
|
1/4
|
3
|

|
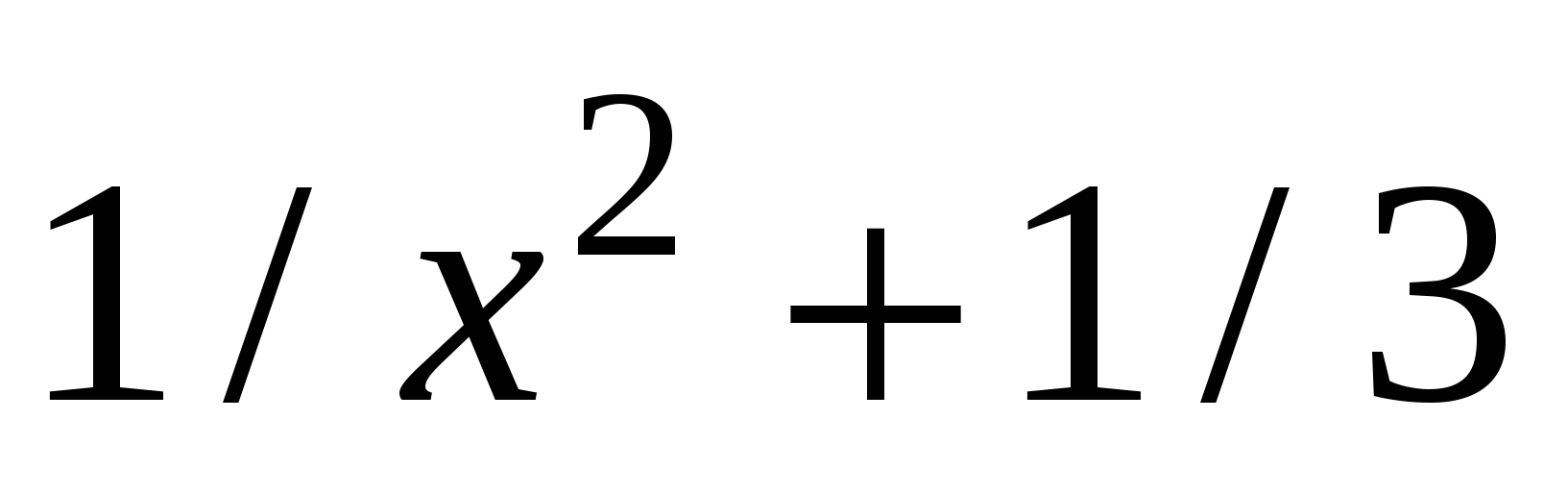
|
-2.5
|
7.5
|
1/5
|
4
|

|
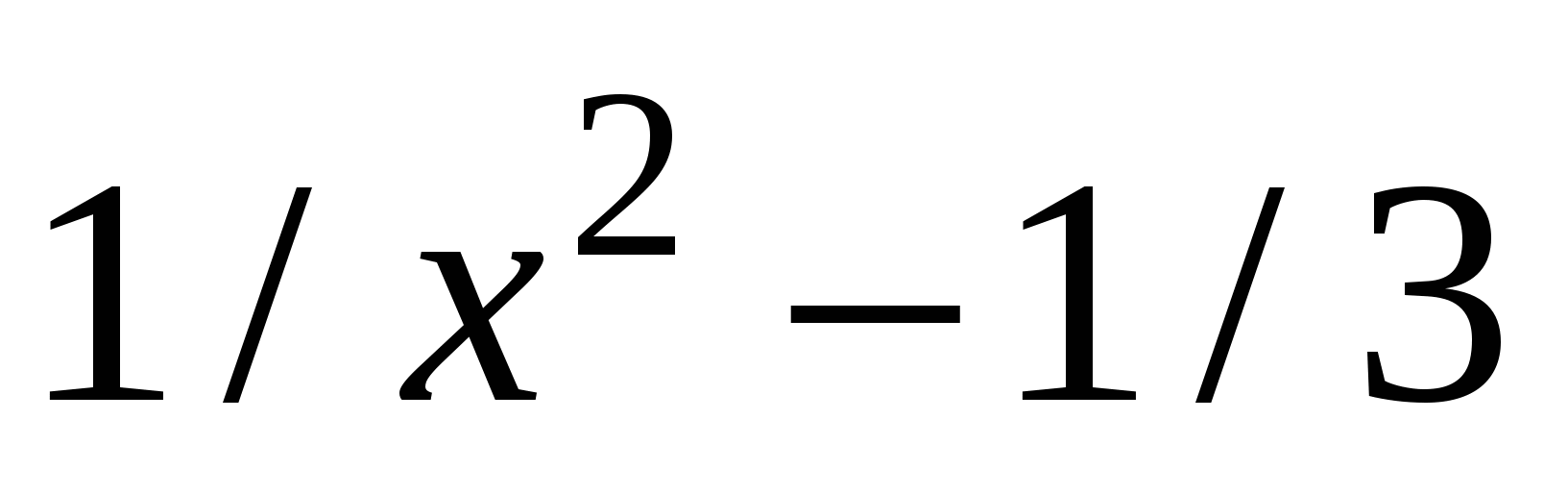
|
3.0
|
-8.0
|
1/6
|
5
|
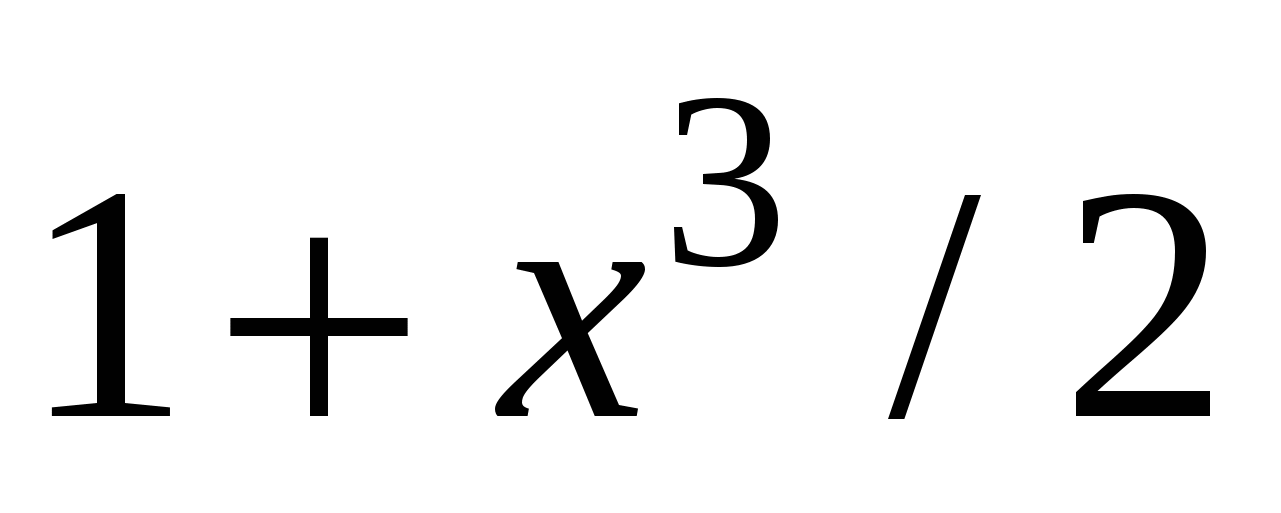
|
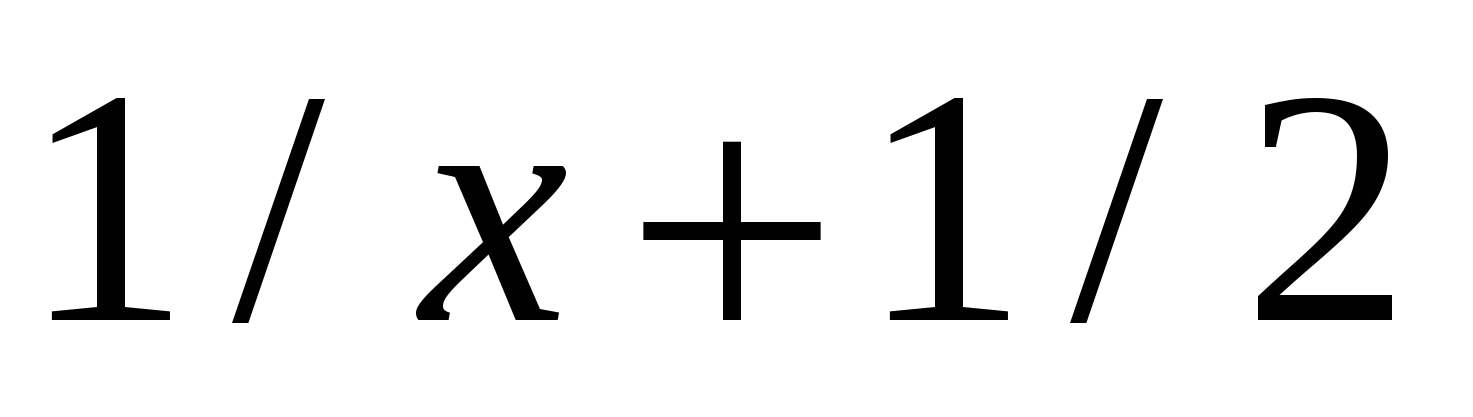
|
-3.5
|
8.5
|
1/7
|
6
|

|
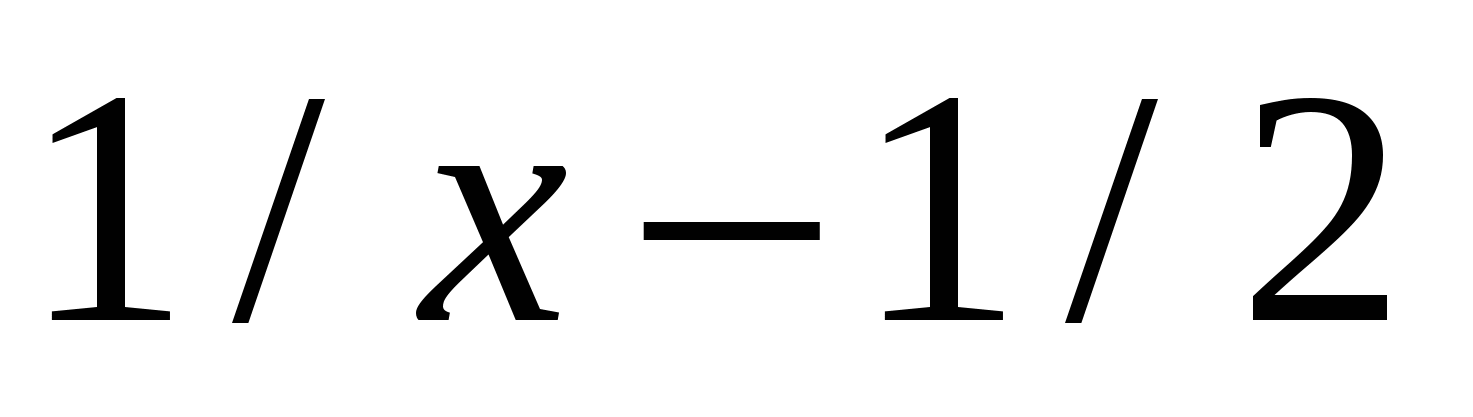
|
4.0
|
-9.0
|
1/8
|
7
|

|

|
-4.5
|
9.5
|
1/9
|
8
|
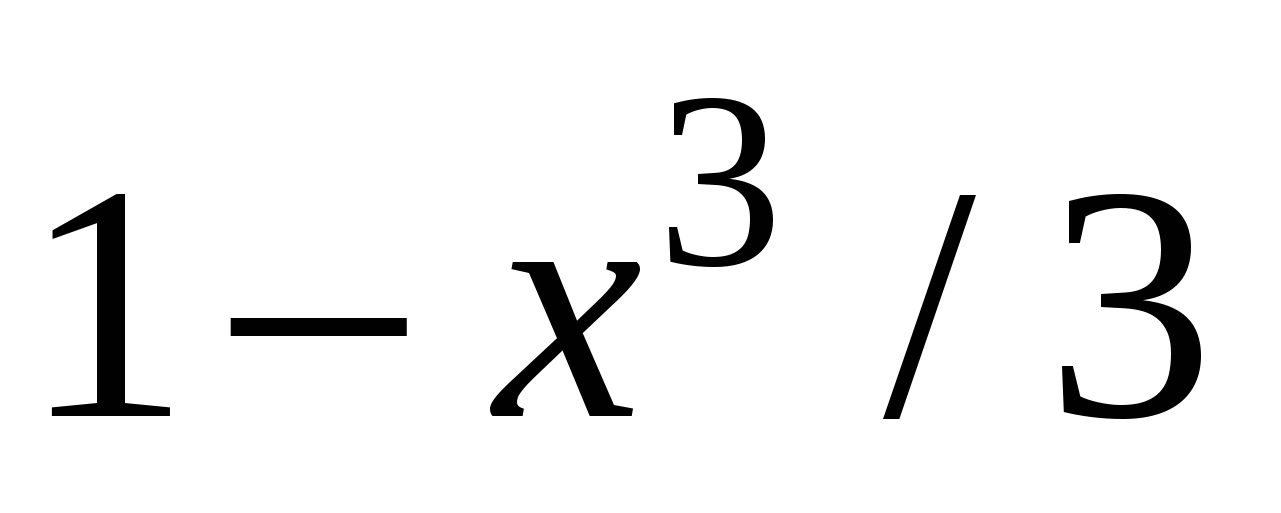
|
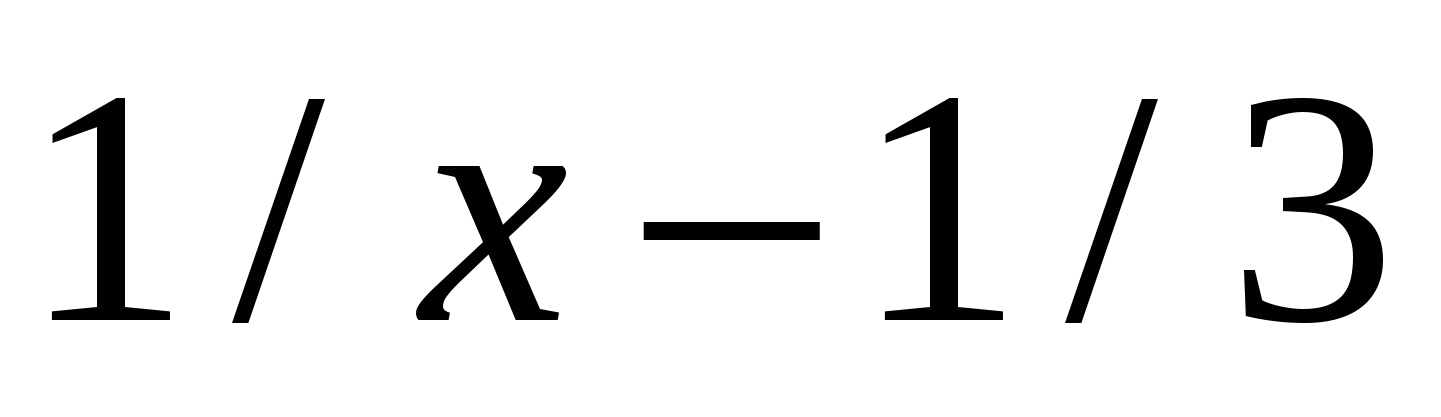
|
5.0
|
-10.0
|
2/9
|
9
|

|
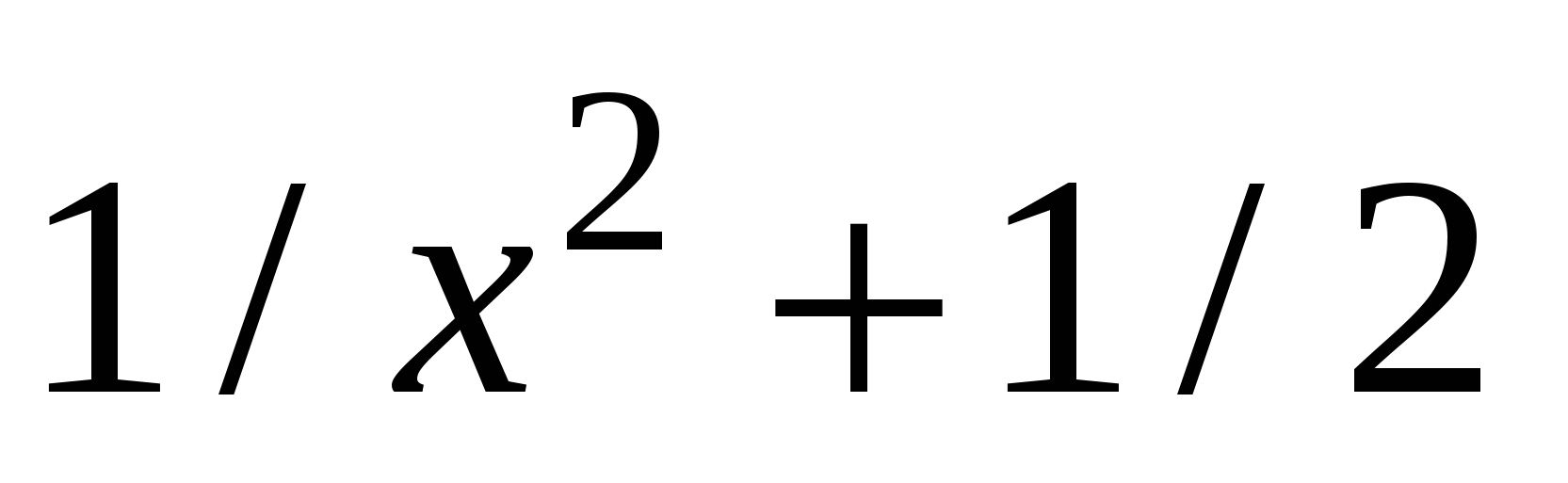
|
-5.5
|
10.5
|
2/3
|
0
|

|
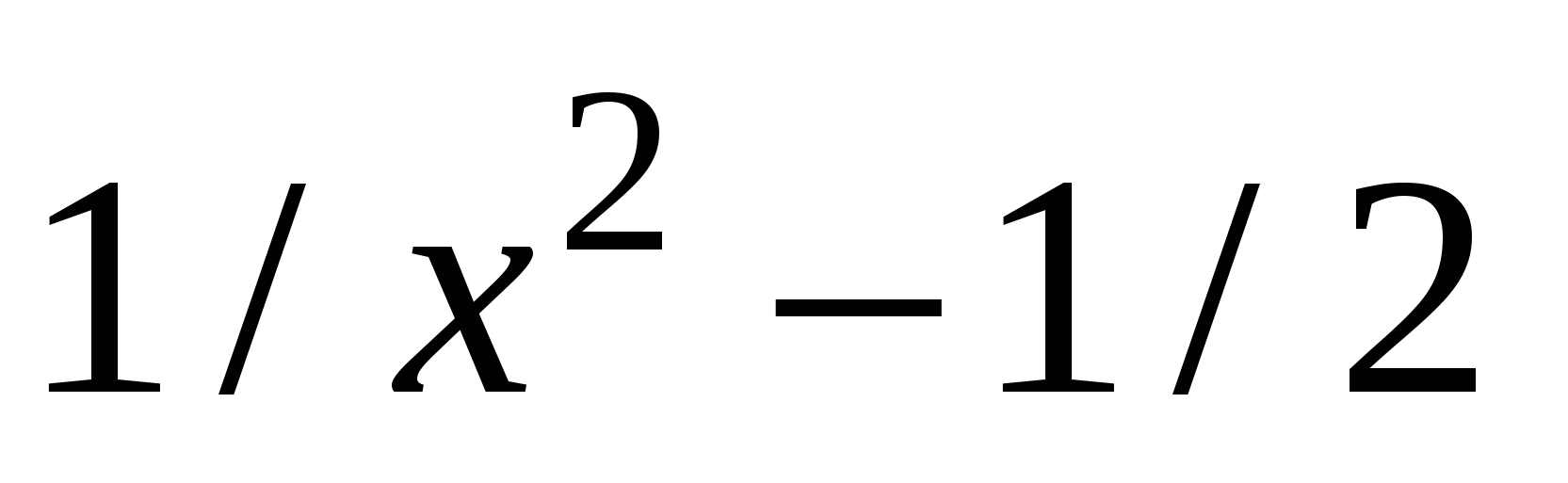
|
6.0
|
-11.0
|
2/5
|
Таблиця 2
Рядок
|
Стовпчик
|
1
|
2
|
3
|
4
|
f1(х1, х2)
|
f2(х1, х2)
|
a
|
b
|
1
|
sin (х1+х2) - х1/b
|
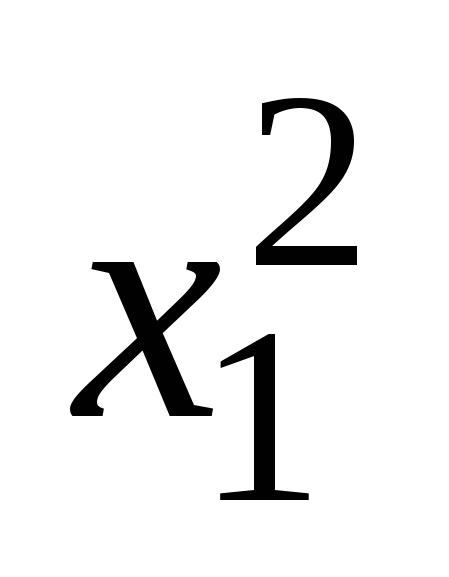 + + 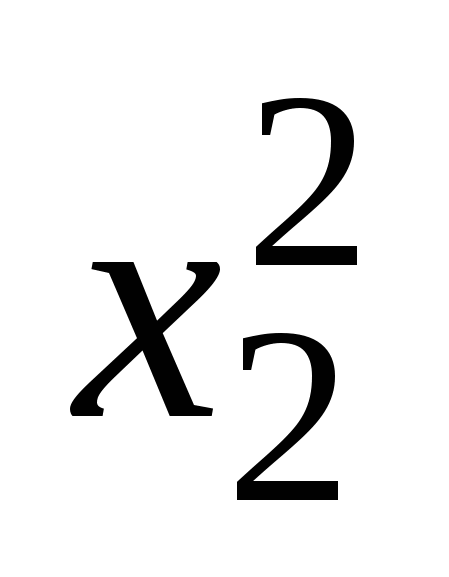 - - 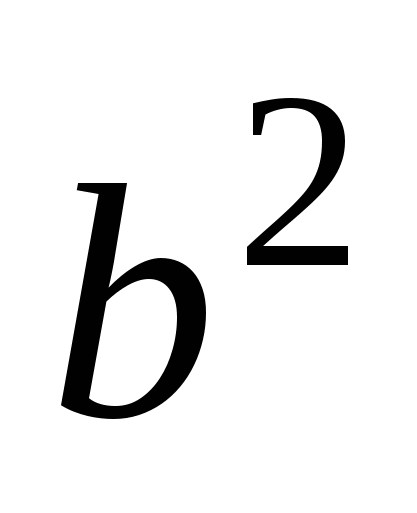
|
1.5
|
6.5
|
2
|
sin (х1-х2) - х1х2 -a/b
|
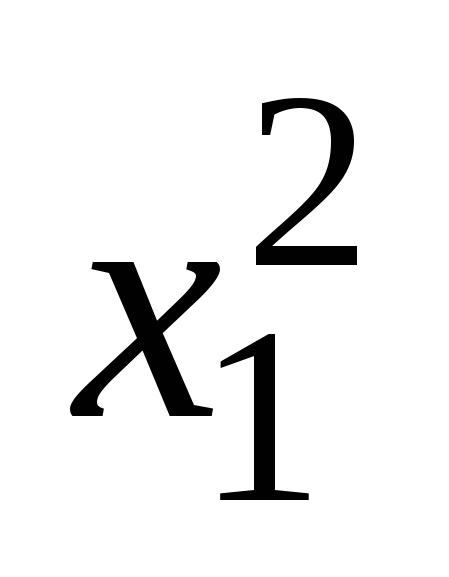 + + 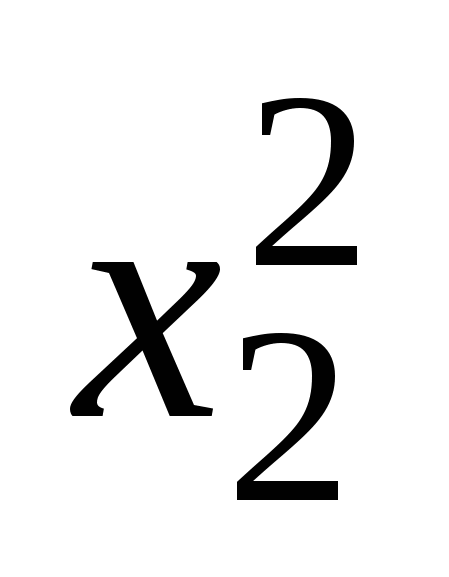 - - 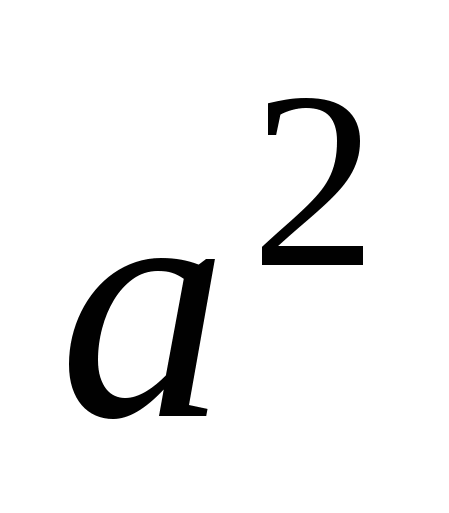
|
2.0
|
7.0
|
3
|
cos (х1+х2) - х2/a
|
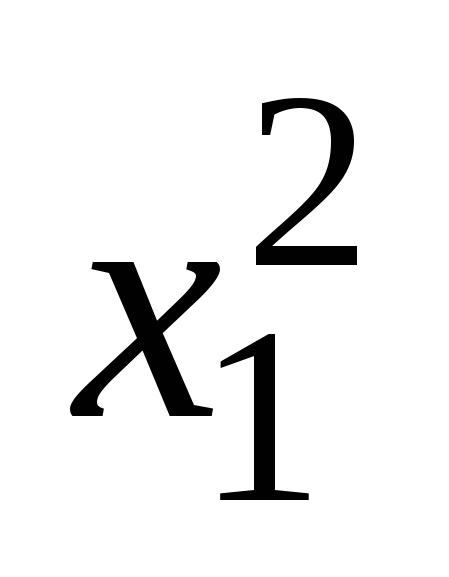 + + 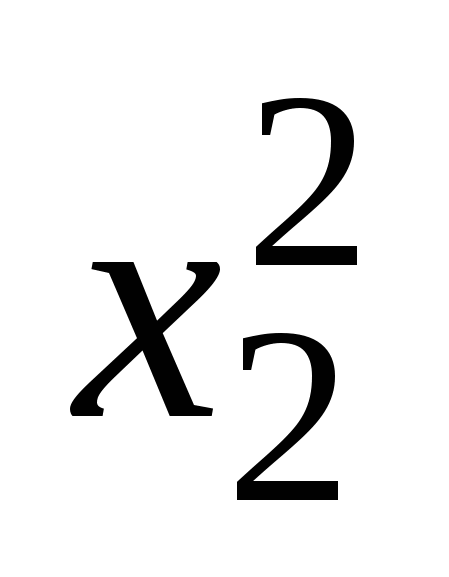 /b - 1 /b - 1
|
2.5
|
7.5
|
4
|
cos (х1-1/a)+х2 -1/b
|
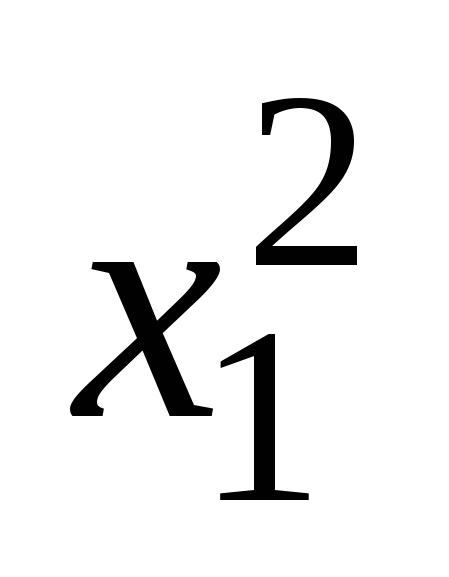 + + 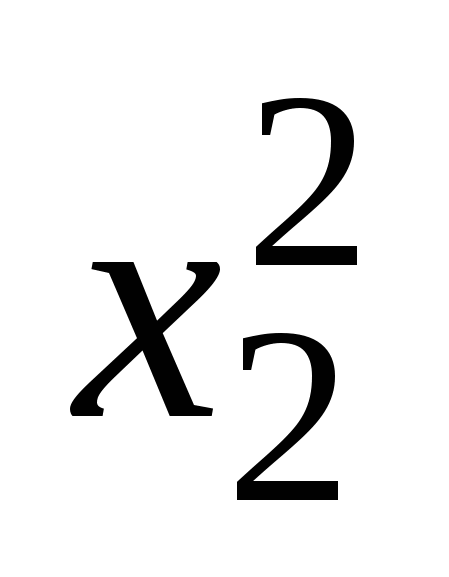 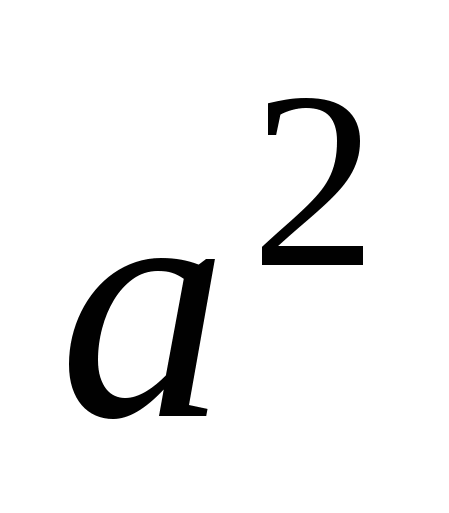 - a/b - a/b
|
3.0
|
8.0
|
5
|
sec (х1х2+a/b) - х1 х1
|
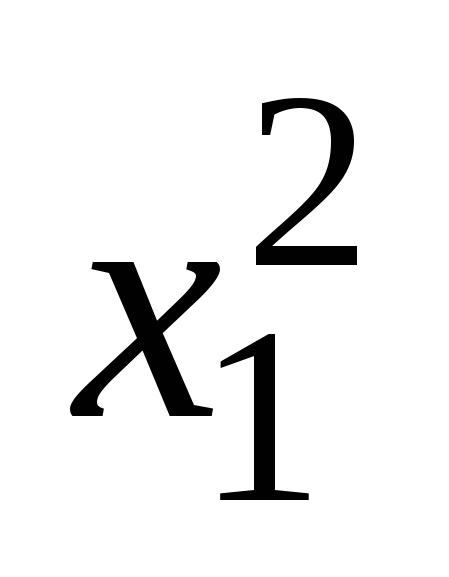 /b + /b + 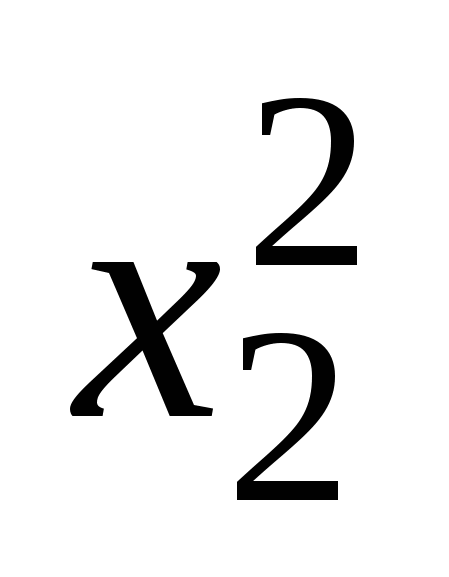 /a - 1 /a - 1
|
3.5
|
8.5
|
6
|
cosec (х1+х2/b) - х2х2
|
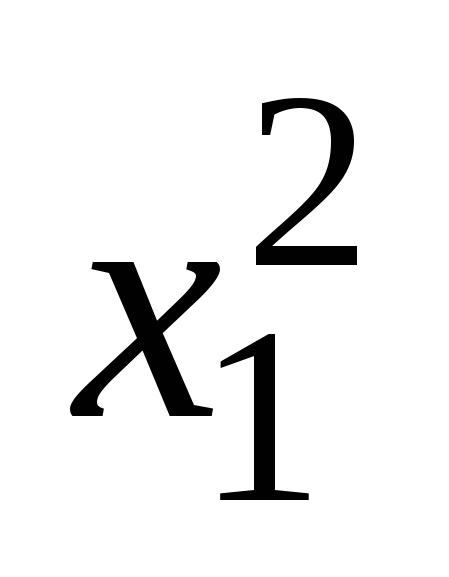 + + 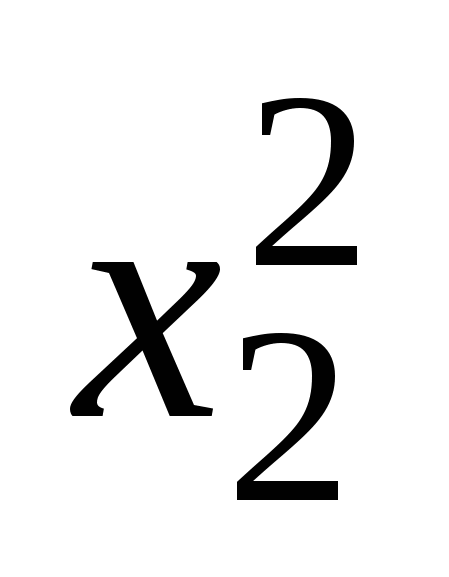 - b/a - b/a
|
4.0
|
9.0
|
7
|
sec (х1 х2-a/b) - х1 х1
|
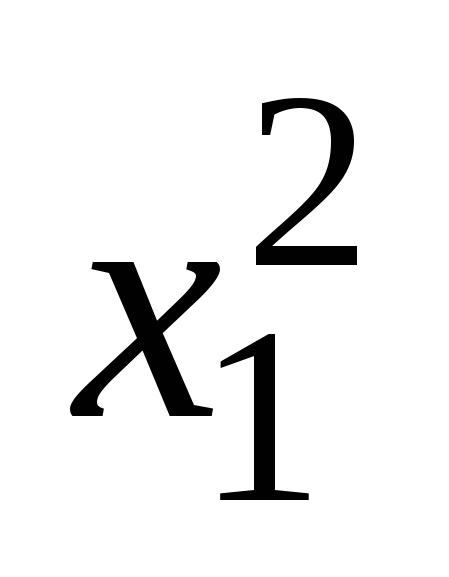 / /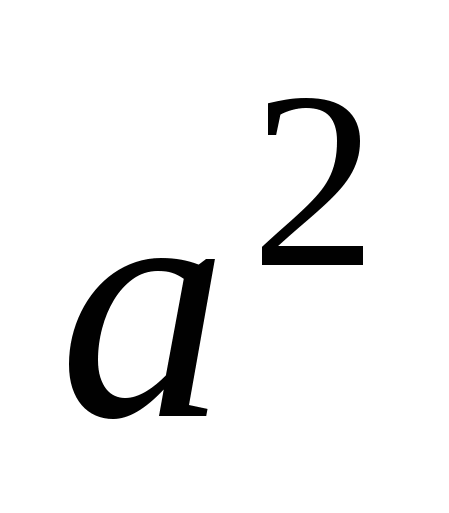 + + 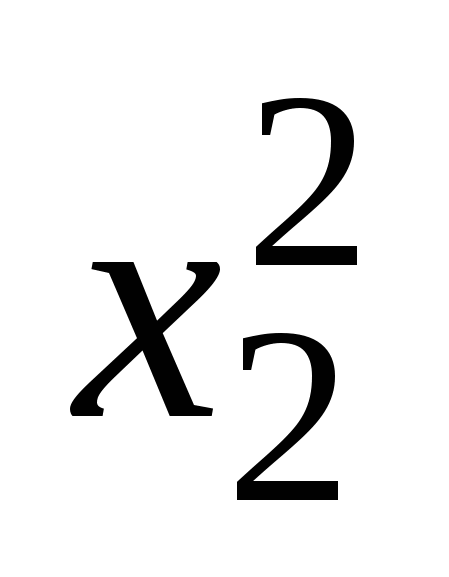 / /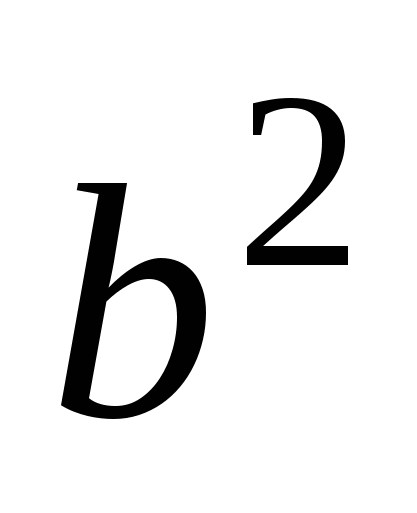 - 1 - 1
|
4.5
|
9.5
|
8
|
sin (х1х2+a/b) - a/b
|
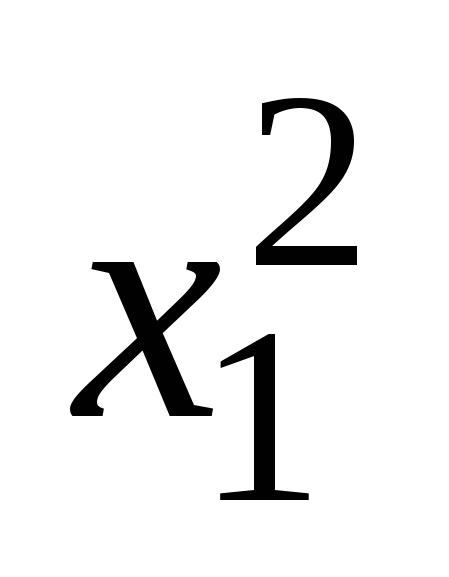 /b + /b + 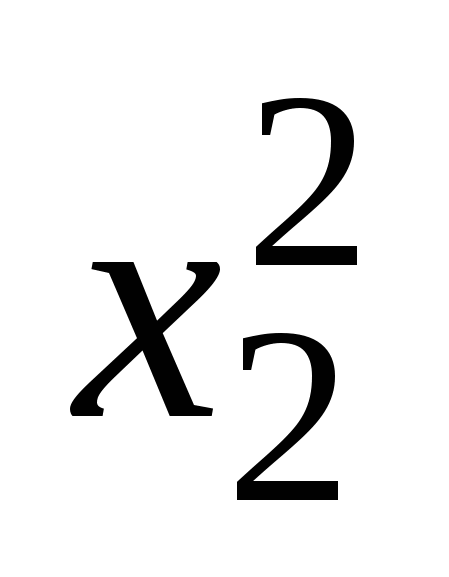 - 1 - 1
|
5.0
|
10.0
|
9
|
cos (х1-a/b)+х2 -1
|
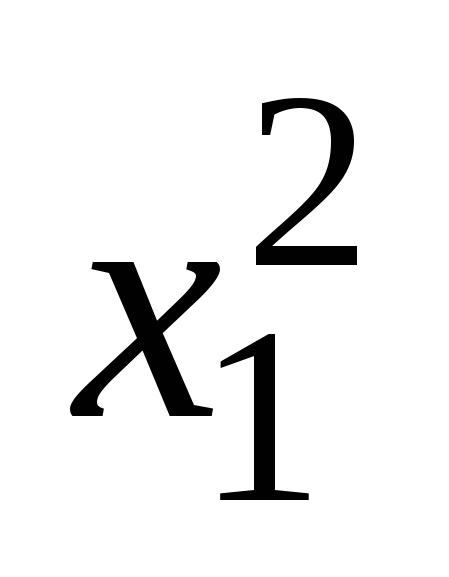 / /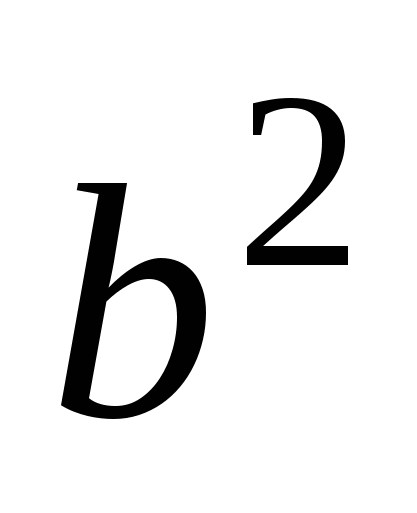 + + 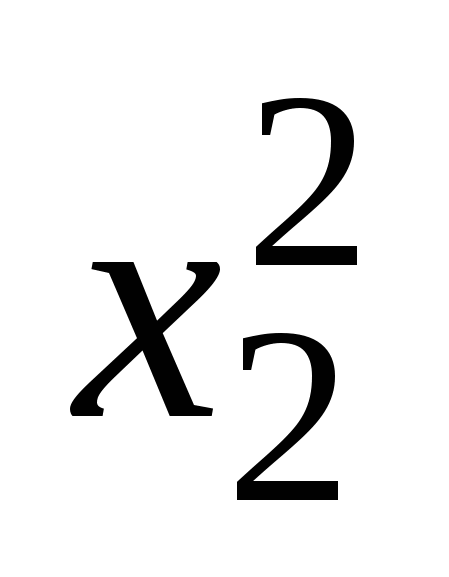 / /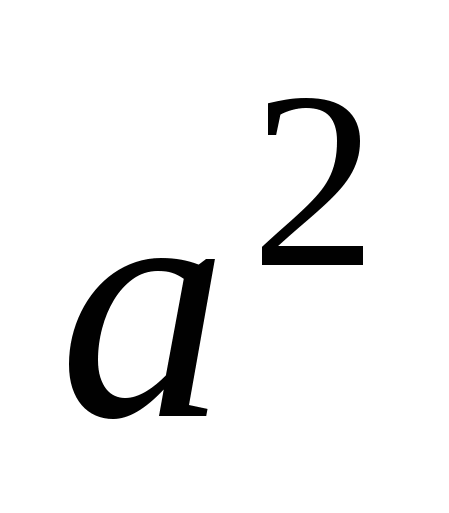 - 1 - 1
|
5.5
|
10.5
|
0
|
cose (х1 х2) - a
|
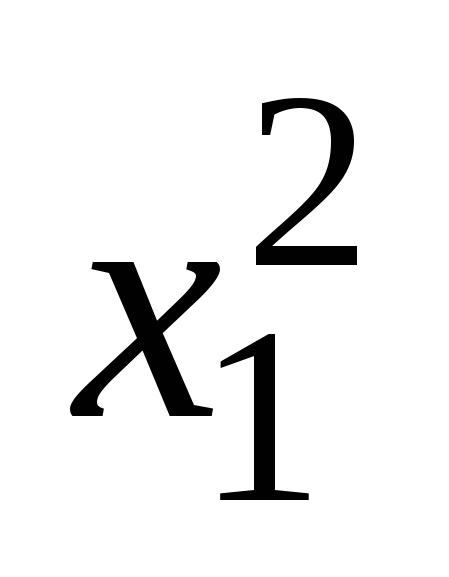 /a + /a + 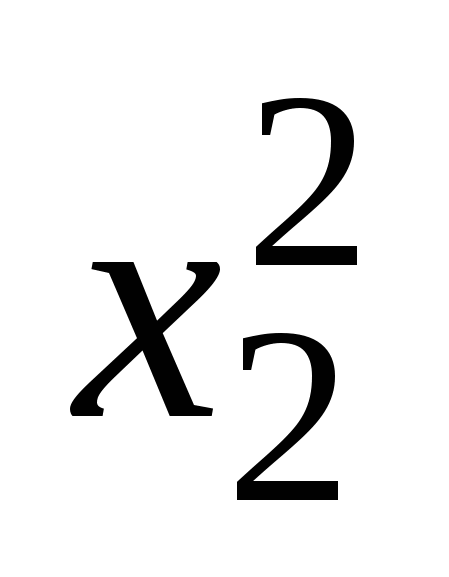 /b - 1 /b - 1
|
6.0
|
11.0
|
Додаток 3
|
|
|
 Скачать 0.83 Mb.
Скачать 0.83 Mb.
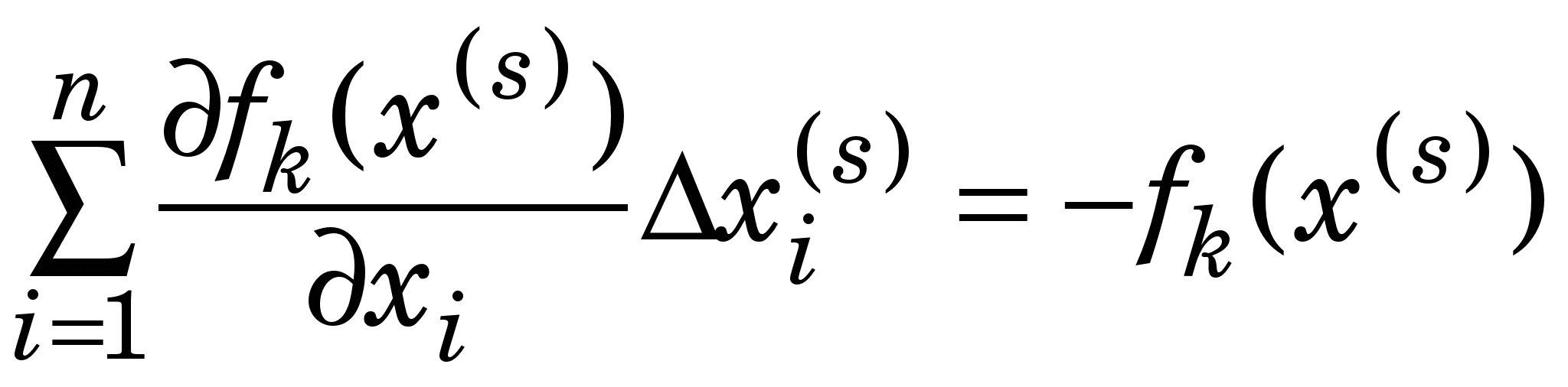
 (3.11)
(3.11)