Опасные факторы пожара. Реферат. Наблюдение как метод исследования. Виды наблюдений. Отличие научного наблюдения от обыденного

• Название: Наблюдение как метод исследования. Виды наблюдений. Отличие научного наблюдения от обыденного
• Анкор: Опасные факторы пожара
• Дата: 16.03.2023
• Размер: 216 Kb.
• Имя файла: Реферат.doc
• Тип: Документы; #995110
• страница: 2 из 4

Газовая среда, заполняющая помещение с проемами (окна, двери и т.п.), как объект исследования есть открытая термодинамическая система.

Эта система взаимодействует с внешней средой путем тепло и массообмена. Будем считать, что в начальной стадии процесса развития пожара через одни проемы выталкиваются из помещения нагретые газы, а через другие поступает холодный воздух. Количество вещества в рассматриваемой открытой термодинамической системе в течение времени изменяется. Термодинамическая система совершает работу, выталкивая нагретые газы во внешнюю атмосферу. Поступление холодного воздуха обусловлено работой проникновения, которую совершает внешняя среда. Эта термодинамическая система взаимодействует также с ограждающими конструкциями путем теплообмена. Кроме того, в эту систему с поверхности горящего материала поступает вещество в виде газообразных продуктов горения. Состояние рассматриваемой термодинамической системы изменяется в результате взаимодействия с окружающей средой. В интегральном методе описания процесса изменения состояния рассматриваемой термодинамической системы, сделаны два допущения.

1. Общие сведения о методах прогнозирования

В современных условиях разработка экономически оптимальных и эффективных противопожарных мероприятий немыслима без научно обоснованного прогноза динамики опасных факторов пожара (ОФП).

Прогнозирование ОФП необходимо:

– при разработке рекомендаций по обеспечению безопасной эвакуации людей при пожаре;

– при создании и совершенствовании систем сигнализации и автоматических систем пожаротушения;

– при разработке оперативных планов тушения (планировании действий подразделений на пожаре);

– при оценке фактических пределов огнестойкости;

– для многих других целей.

Современные методы прогнозирования ОФП не только позволяют «заглядывать в будущее», но и дают возможность снова «увидеть» то, что уже когда-то и где-то произошло. Другими словами, теория прогнозирования позволяет воспроизвести картину развития реально произошедшего пожара. Это необходимо, например, при криминалистической или пожарно-технической экспертизе пожара.

Опасными факторами пожара, воздействующими на людей и имущество, (согласно ФЗ РФ № 123-ФЗ «Технический регламент о требованиях пожарной безопасности») являются:

– пламя и искры,

– тепловой поток,

– повышенная температура окружающей среды,

– повышенная концентрация токсических продуктов горения и термического разложения,

– пониженная концентрация кислорода,

– снижение видимости в дыму.

С научных позиций ОФП являются физическими понятиями и, следовательно, каждый из них представлен в количественном отношении одной или несколькими физическими величинами. С этих позиций рассмотрим вышеперечисленные ОФП.

Первый опасный фактор – пламя. Пламя – это видимая часть пространства (пламенная зона), внутри которой протекает процесс окисления (горения) и происходит тепловыделение, а также генерируются токсичные газообразные продукты и поглощается забираемый из окружающего пространства кислород. Кроме того, в границах этой части пространства (зоны) образуется специфическая дисперсная среда, особые оптические свойства которой обусловлены процессами рассеивания энергии световых волн вследствие их многократного отражения от мельчайших твердых (и жидких) частиц. Этот процесс образования дисперсной среды, ухудшающей видимость, принято называть процессом дым образования.

По отношению к объему помещения, заполненному газом, пламенную зону, с одной стороны, можно рассматривать как источник тепловой энергии и токсичных продуктов горения, а также мельчайших твердых (жидких) частиц, из-за которых ухудшается видимость. С другой стороны, пламенную зону можно рассматривать как «сток», в который уходит кислород из помещения.

В связи с вышесказанным содержание понятия «пламя» представлено в количественном отношении следующими величинами:

– характерными размерами пламенной зоны (очага горения), например площадью горения (площадью пожара) FГ, м2;

– количеством сгорающего (окисляемого) за единицу времени горючего материала (ГМ) (скоростью выгорания) ψ, кг·с−1;

– мощностью тепловыделения Qпож, Вт (Qпож = ψ РНQ , где РНQ – теплота сгорания, Дж·кг−1);

– количеством генерируемых за единицу времени в пламенной зоне токсичных газов ψLi, кг·с−1, где Li – количество i-го токсичного газа, образующегося при сгорании единицы массы ГМ;

– количеством кислорода, потребляемого в зоне горения, ψL1, кг·с−1, где L1 – количество кислорода, необходимое для сгорания (окисления) единицы массы ГМ;

– оптическим количеством дыма, образующегося в очаге горения, ψD, Нп·м2·с−1, где D – дымообразующая способность горючего материала, Нп·м2·кг−1.

Второй опасный фактор – плотность теплового потока q. Этот фактор количественно характеризуется величиной теплового потока, приходящегося на единицу поверхности тела человека или на единицу поверхности материалов, приборов, оборудования, ограждающих конструкций, Вт/м2.

Третий опасный фактор – повышенная температура среды. Температура среды, заполняющей помещение, является параметром состояния. Физическое содержание этого параметра рассмотрено в книге «Термодинамика и теплопередача в пожарном деле» [17], он обозначается Т, если используется размерность по Кельвину, или t, если используется размерность по Цельсию.

Четвертый опасный фактор – токсичные продукты горения. Этот фактор количественно характеризуется парциальной плотностью (или концентрацией) каждого токсичного газа.

Парциальная плотность компонентов газовой среды в помещении является параметром состояния. Обозначается ρ, размерность – кг·м−3. Сумма парциальных плотностей всех компонентов газовой среды равна плотности газа ρ. Концентрацией i-го токсичного газа xi обычно называют отношение парциальной плотности этого газа ρi к плотности газа ρ, т. е.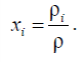


Если умножить отношение 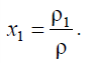на 100, то получим значение концентрации продукта в процентах. Пятый опасный фактор – пониженная концентрация кислорода в помещении. Этот фактор количественно характеризуется значением парциальной плотности кислорода ρ1 или отношением ее к плотности газовой среды в помещении, т. е.



Шестой опасный фактор пожара – снижение видимости в дыму. Этот фактор количественно представляют параметром, называемым оптической концентрацией дыма. Этот параметр обозначают μ, его размерность –Нп·м−1. (Иногда параметр μ называют натуральным показателем ослабления.) Расстояние видимости в дыму lвид и оптическая концентрация дымасвязаны между собой простым соотношением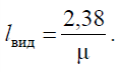



Вышеприведенные величины: температура среды, парциальные плотности (концентрации) токсичных газов и кислорода, оптическая плотность дыма – являются параметрами состояния среды, заполняющей помещение при пожаре.

Они характеризуют свойства газовой среды в помещении. Начиная с возникновения пожара в процессе его развития эти параметры состояния непрерывно изменяются во времени, τ, т. е.

T = f1(τ); ρ1 = f2(τ); μ = f3(τ); O2 ρ = f4(τ).

Совокупность этих зависимостей составляет суть динамики ОФП. При рассмотрении воздействия ОФП на людей используются так называемые предельно допустимые значения параметров состояния среды в зоне пребывания людей (рабочей зоне).

Предельно допустимые значения ОФП получены в результате обширных медико-биологических исследований, в процессе которых установлен характер воздействия ОФП на людей в зависимости от значений количественных характеристик ОФП. Так, например, установлено, что если концентрация кислорода О2 уменьшится вдвое по сравнению с нормальной концентрацией его в воздухе (нормальная концентрация составляет 23 %, т. е. приблизительно 270 г О2 в м3 воздуха), т. е. будет составлять 135 г О2 в м3 воздуха, то нарушается деятельность сердечно-сосудистой системы и органов дыхания человека, а также он теряет способность реальной оценки событий. При уменьшении концентрации кислорода в 3 раза по сравнению с нормальной концентрацией останавливается дыхание и через 5 мин останавливается работа сердца.

Следует подчеркнуть, что в условиях пожара имеет место одновременное воздействие на человека всех ОФП. Вследствие этого опасность многократно увеличивается. Предельно допустимые значения ОФП указаны в ФЗ РФ №123-ФЗ и ГОСТ 12.1.004–91. Ниже они представлены в виде таблицы.



При рассмотрении воздействия ОФП на элементы конструкций и оборудование используются критические значения параметров, характеризующих термическое воздействие пожара на них. Например, при оценке воздействия пожара на железобетонные конструкции применяется понятие критического значения температуры арматуры этих конструкций. Обычно считается, что при нагревании арматуры до температуры, равной 400–450 °С, происходит разрушение железобетонной конструкции. При оценке воздействия пожара на остекление предполагается, что при температуре газовой среды в помещении, равной 300–350 °С, будет происходить разрушение остекления.

Современные научные методы прогнозирования ОФП основываются на математическом моделировании, т. е. на математических моделях пожара. Математическая модель пожара описывает в самом общем виде изменение параметров состояния среды в помещении в течение времени, а так-же изменение параметров состояния ограждающих конструкций этого помещения и различных элементов технологического оборудования.

Основные уравнения, из которых состоит математическая модель пожара, вытекают из фундаментальных законов природы – первого закона термодинамики, закона сохранения массы и закона сохранения импульса.

Эти уравнения отражают и увязывают всю совокупность взаимосвязанных и взаимообусловленных процессов, присущих пожару, таких, как тепловыделение в результате горения, дымовыделение в пламенной зоне, изменение оптических свойств газовой среды, выделение и распространение токсичных газов, газообмен помещения с окружающей средой и со смежными помещениями, теплообмен и нагревание ограждающих конструкций, снижение концентрации кислорода в помещении.

Методы прогнозирования ОФП различают в зависимости от вида математической модели пожара. Математические модели пожара в помещении условно делятся на три класса (три вида): интегральные, зонные, полевые (дифференциальные). Интегральная модель пожара позволяет получить информацию, т. е. сделать прогноз о средних значениях параметров состояния среды в помещении для любого момента развития пожара. При этом для того чтобы сопоставлять (соотносить) средние (т. е. среднеобъемные) параметры среды с их предельными значениями в рабочей зоне, используются формулы, полученные на основе экспериментальных исследований пространственного распределения температур, концентраций продуктов горения, оптической плотности дыма и т. д.

Зонная модель позволяет получить информацию о размерах характерных пространственных зон, возникающих при пожаре в помещении, и средних параметрах состояния среды в этих зонах. В качестве характерных пространственных зон можно выделить, например, в начальной стадии пожара припотолочную область пространства, область восходящего над очагом горения потока нагретых газов и область незадымленной холодной части пространства. Полевая (дифференциальная) модель позволяет рассчитать для любого момента развития пожара значения всех локальных параметров состояния во всех точках пространства внутри помещения. Перечисленные модели отличаются друг от друга объемом той информации, которую они могут дать о состоянии газовой среды в помещении и взаимодействующих с нею конструкций на разных этапах (стадиях) пожара. В этом отношении наиболее детальные сведения можно получить с помощью полевой модели.

В математическом отношении три вышеназванных вида моделей пожара характеризуются разным уровнем сложности. Интегральная модель пожара в своей основе представлена системой обыкновенных дифференциальных уравнений. Искомыми функциями выступают среднеобъемные параметры состояния среды, независимым аргументом является время τ. Основу зонной модели пожара в общем случае составляет совокупность нескольких систем обыкновенных дифференциальных уравнений. Параметры состояния среды в каждой зоне являются искомыми функциями, а независимым аргументом – время τ. Искомыми функциями являются так-же координаты, определяющие положение границ характерных зон.

Наиболее сложной в математическом отношении является полевая модель. Ее основу составляет система уравнений в частных производных, описывающих пространственно-временное распределение температур и скоростей газовой среды в помещении, концентраций компонентов этой среды (кислород, оксид и диоксид углерода и т. д.), давлений и плотностей. Эти уравнения включают реологический закон Стокса, закон теплопроводности Фурье, закон диффузии, закон радиационного переноса и т. п.

В более общем случае к этой системе уравнений добавляется дифференциальное уравнение теплопроводности, описывающее процесс нагревания ограждающих конструкций. Искомыми функциями в этой модели являются плотность и температура среды, скорость движения газа, концентрации компонентов газовой среды, оптическая плотность дыма (натуральный показатель ослабления света в дисперсной среде) и т. д. Независимыми аргументами являются координаты х, у, z и время τ.

Следует подчеркнуть, что основные дифференциальные уравнения всех названных математических моделей пожара вытекают из неопровержимых фундаментальных законов природы. В с вязи с этим уместно указать, что основные дифференциальные уравнения интегральной модели пожара можно получить, например, из уравнений полевой (дифференциальной) модели путем интегрирования последних по объему помещения.

Следовательно, в принципе, результаты вычислений искомых функций, с которыми оперирует та или иная модель пожара, должны были бы иметь одинаковую степень достоверности. Однако адекватность результатов расчетов реальному пожару определяется не только системой основных (базовых) уравнений каждой модели пожара. Дело в том, что в каждой модели привлекаются дополнительные функциональные зависимости для вычисления тех или иных физических величин, содержащихся в математическом описании пожара.

Например, в полевой модели могут привлекаться различные дополнительные уравнения для вычисления коэффициентов турбулентного переноса энергии, импульса и компонентов газовой среды. В интегральной и зонной моделях могут использоваться различные формулы для вычисления тепловых потоков в ограждающие конструкции. Поэтому при оценке достоверности результатов прогнозирования необходимо прежде всего учитывать уровень научных разработок вопросов, определяющих содержание дополнительных функциональных зависимостей.

Чтобы сделать научно обоснованный прогноз, обращаются к той или иной модели пожара. Выбор модели определяется целью (задачами) прогноза. Путем решения системы дифференциальных уравнений, которые составляют основу выбранной математической модели, устанавливают конкретный характер динамики ОФП.

Следует отметить, что даже при использовании интегральной модели пожара получить аналитическое решение присущей этой модели системы обыкновенных дифференциальных уравнений в общем случае невозможно. В силу сказанного реализация вышеназванных методов прогнозирования возможна лишь путем численного решения системы дифференциальных уравнений, присущих выбранной модели пожара. Это численное решение можно выполнить только с помощью современных компьютеров. Именно поэтому разработка и реализация математических моделей пожара началась сравнительно недавно.

Интегральная модель пожара как в своей основе, так и в деталях была разработана в середине 70-х гг. прошлого века и опубликована в 1976 г. одним из авторов этой книги Ю. А. Кошмаровым (труды ВНИИПО, научные отчеты ВИПТШ). Спустя год после этой публикации японским исследователем Т. Танака была напечатана статья на эту тему (Takeyoshi Tanaka «A Mathematical model of a compartment fire un modele mathematique de l'incendie d'une piece»). Статья Т. Танака повторяла опубликованное проф. Ю. А. Кошмаровым, содержала ряд погрешностей и носила незавершенный характер. Существенное развитие и дополнение получила интегральная математическая модель пожара в работах учеников проф. Ю. А. Кошмарова – А. В. Матюшина, С. И. Зернова, В. М. Астапенко, Ю. С. Зотова, А. Н. Шевлякова, И. Д. Гуско, В. А. Козлова и др. В частности, интегральная модель пожара была дополнена дифференциальным уравнением, описывающим изменение оптической концентрации дыма в помещении при пожаре.

Первая зонная модель пожара была предложена в диссертации польского инженера Е. Воланина, выполненной под руководством проф. Ю. А. Кошмарова. В последующие годы зонные модели получили существенное развитие в работах Е. Воланина и В. Н. Тимошенко и др.

Полевая модель пожара впервые в законченном виде (для ограниченных условий) была реализована в диссертации A. M. Рыжова, выполненной в 1982–1985 гг. под руководством проф. Ю. А. Кошмарова. Эта модель разрабатывалась в последующие годы И. Ф. Астаховой и рядом иностранных исследователей. Существенный вклад в развитие метода прогнозирования параметров пожара на основе полевой модели внес также за последние годы A. M. Рыжов, продолживший работу, начатую еще в кандидатской диссертации, а также проф. В. Л. Страхов и С. В. Пузач.