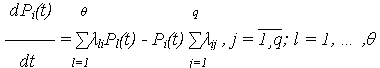НЭК. Л.р №7, Гатина А.А., гр.№3712, НЭК.. Надежность восстанавливаемых резервированных систем
 Скачать 269.5 Kb. Скачать 269.5 Kb.
|
|
Лабораторная работа №7 Тема: Надежность восстанавливаемых резервированных систем Цель работы: определить количественные характеристики надежности восстанавливаемых резервированных систем. Задание:   Решение: Составили надежностную схему и определили критерии отказа системы. 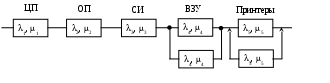 Установили, что отказ системы наступил при отказе любой из ее подсистем: ЦП, ОП, СИ, ВЗУ или Принтеров, а отказ подсистемы ВЗУ и принтеров наступил при отказе всех (двух) входящих в нее устройств. Определили по справочникам и условиям эксплуатации значения li и mi для отдельных устройств.
Значения m выбраны, исходя из типовых условий эксплуатации компьютера: легче всего произвести замену отказавших модулей ОП ТВ=1 час, ремонт ЦП, СИ требует замены системной платы ТВ=10 ч, так же оценены затраты времени на ремонт винчестера. Ремонт принтера выполняется в специализированных фирмах, поэтому для него ТВ=100 ч. Расчет характеристик подсистемы ВЗУ. В соответствии с выражениями для «горячего» резервирования для m=2 имеем: m=2m4=0,2 1/ч, КГ=1-(1- КГ4)2=1-10-6, l=m(1- КГ)=2*10-7 1/ч. Расчет характеристик подсистемы принтеров. В соответствии с выражениями для скользящего резервирования для m=2 и r=1 имеем: m=2m5=0,02 1/ч l=m(1- КГ)=0,02*0,01=2*10-4 1/ч. Расчет характеристик всей системы. В соответствии с выражением для последовательного включения устройств и подсистем имеем: lS=10-5+10-4+10-6+2*10-7+2*10-4=3*10-4 1/ч, КГS= mS=l/(1-КГ)=0,03 1/ч Результат расчета для системы: Т=1/lS=3300 ч, Тн=1/mS=33 ч, КГS=0,99, если бы в системе не было резервирования отдельных наименее надежных устройств, то Вывод: определили количественные характеристики надежности восстанавливаемых резервированных систем. Контрольные вопросы 1. Перечислите основные показатели надежности восстанавливаемых резервированных систем. Для восстанавливаемых резервированных систем показателями надежности являются комплексные показатели, то есть коэффициенты готовности Кг и простоя КП. 2. В каком случае произойдет отказ резервированной группы с восстановлением? Отказ резервированной группы с восстановлением произойдет, если все элементы, составляющие группу, ремонтируются. 3. Какие виды резервирования применяются для повышения надежности техники? Резерв времени можно использовать для устранения отказа элемента. Если отказ устранен до истечения резерва времени, то он не переходит в отказ системы, чем обеспечивается просеивание потока отказов и повышение надежности техники. 4. При каком виде резервирования достигается наибольший выигрыш надежности? При пассивном резервировании наибольший выигрыш в надежности достигается в ТС с неизменной нагрузкой, наименьший – с резервированием по нагрузке. Здесь следует подчеркнуть, что в ТС с активным резервированием происходит нарушение работы объекта на время с момента отказа основного элемента до момента включения резервного. Таким образом, если такой перерыв в работе ТС принципиально недопустим, то, следовательно, метод пассивного резервирования является единственно возможным. И это один из самых существенных моментов, на который разработчик ТС должен обратить свое внимание при выборе между активным и пассивным методами резервирования. 5. В каком порядке выполняется расчет надежности восстанавливаемой дублированной системы методом дифференциальных уравнений? Метод дифференциальных уравнений. Метод применяется для оценки надежности восстанавливаемых объектов и основан на допущении о показательных распределениях времени между отказами (наработки) и времени восстановления. При этом параметр потока отказов w = λ =1/tcp. и интенсивность восстановления µ = 1/tв, где tcp. – среднее время безотказной работы, tв – среднее время восстановления. 6. В каких состояниях может находиться восстанавливаемая дублированная система? Дублированная система может находиться в трех состояниях: "0" - обе системы (цепи) работоспособны; "1" - одна цепь восстанавливается, другая работоспособна; "2" - обе цепи восстанавливаются. С точки зрения выполнения функциональных задач, возложенных на систему, состояние "2" соответствует отказу. 7. 8. Нарисуйте граф состояний для восстанавливаемой дублированной системы, имеющей нагруженный резерв, при восстановлении без ограничений. Граф состояний для восстанавливаемой дублированной системы, имеющей ненагруженный резерв и ограниченное восстановление. 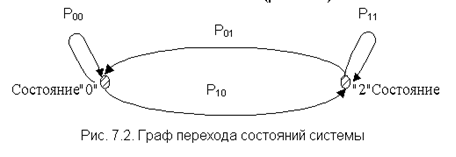 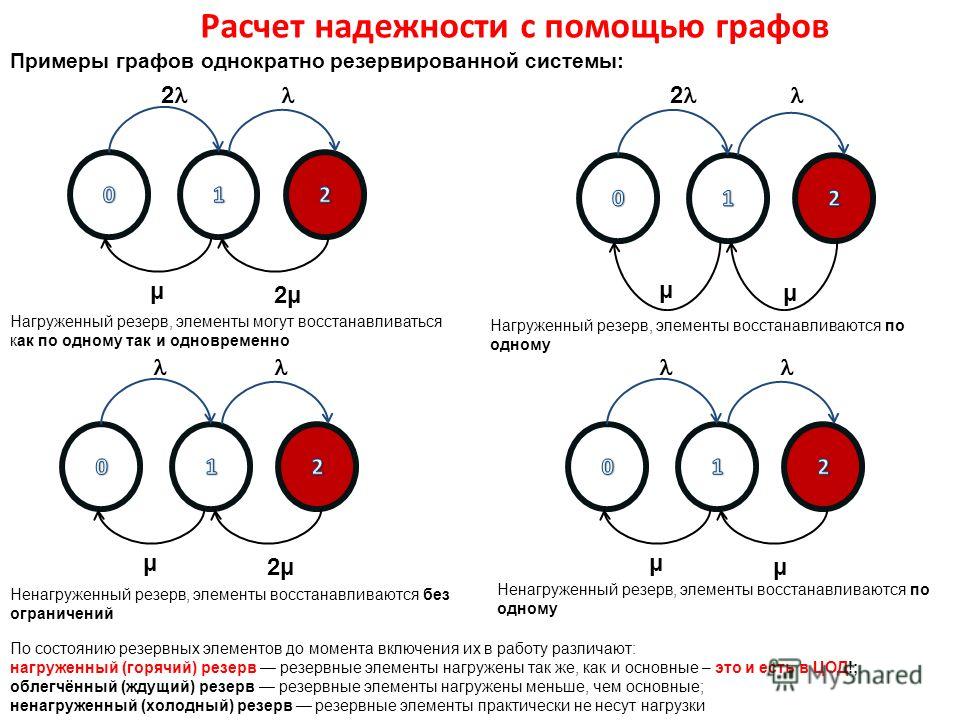 9. Приведите правила составления системы дифференциальных уравнений для вероятностей состояний восстанавливаемых систем. Основные правила составления модели: 1. Математическую модель изображают в виде графа состояний. Элементы графа: а) кружки (вершины графа S1 , S2 , … , Sn ) – возможные состояния системы S, возникающие при отказах элементов; б) стрелки – возможные направления переходов из одного состояния Si в другое Sj . Над/под стрелками указываются интенсивности переходов. Примеры графа: 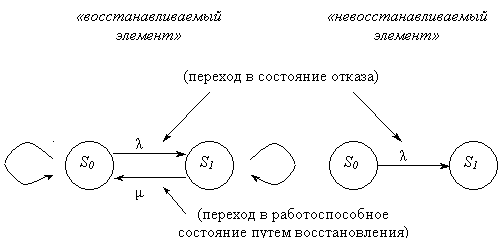 S0 – работоспособное состояние; S1 – состояние отказа. «Петлей» обозначаются задержки в том или ином состоянии S0 и S1 соответствующие: - исправное состояние продолжается; - состояние отказа продолжается (в дальнейшем петли на графах не рассматриваем). Граф состояний отражает конечное (дискретное) число возможных состояний системы S1 , S2 , … , Sn. Каждая из вершин графа соответствует одному из состояний. 2. Для описания случайного процесса перехода состояний (отказ/ восстановление) применяют вероятности состояний P1(t), P2(t), … , Pi(t), … , Pn(t), где Pi(t) – вероятность нахождения системы в момент t в i-м состоянии, т. е. Pi(t) = P{S(t) = si}. Очевидно, что для любого t
(нормировочное условие, поскольку иных состояний, кроме S1 , S2 , … , Sn нет). 3. По графу состояний составляется система обыкновенных дифференциальных уравнений первого порядка (уравнений Колмогорова-Чепмена), имеющих вид:
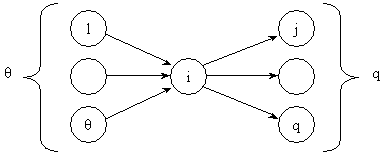 В общем случае, интенсивности потоков При составлении дифференциальных уравнений пользуются простым мнемоническим правилом: а) в левой части – производная по времени t от Pi(t); б) число членов в правой части равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями; в) каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка; г) знак произведения положителен, если стрелка входит (направлена острием) в рассматриваемое состояние, и отрицателен, если стрелка выходит из него. Проверкой правильности составления уравнений является равенство нулю суммы правых частей уравнений. 4. Чтобы решить систему дифференциальных уравнений для вероятностей состояний P1(t), Pi(t), … , Pn(t) необходимо задать начальное значение вероятностей P1(0), Pi(0), … , Pn(0), при t = 0, сумма которых равна единице: Если в начальный момент t = 0 состояние системы известно, например, S(t=0) = Si, то Pi(0) = 1, а остальные равны нулю. 10. Какой вид резервирования применяется на практике наиболее часто? На практике наиболее часто применяется резервирование с постоянно включенным резервом. 11. 12. Запишите формулы для определения наработки на отказ и коэффициента готовности восстанавливаемых систем при ненагруженном и нагруженном дублировании и неограниченном восстановлении.  13. Что такое коэффициент простоя? Какой зависимостью связаны коэффициент простоя и коэффициент готовности? Коэффициентом простоя называется отношение времени восстановления к сумме времен наработки на отказ и времени восстановления взятых за один и тот же календарный срок. Кп= tв/( tср.+ tв), Коэффициент готовности и коэффициент простоя связанны между собой зависимостью. Кп=1-Кг. 14. Во сколько раз повышается надежность восстанавливаемой дублированной системы, если время восстановления в 100 раз меньше наработки на отказ? Ответ: в 10-2 раз повышается надежность восстанавливаемой дублированной системы. | |||||||||||||||||||||||||||||||