Наибольших успехов в этом достигли технические науки и производственные процессы механика и машиностроение, электротехника, строительное дело, транспорт и ряд других
 Скачать 319.5 Kb. Скачать 319.5 Kb.
|
|
Специфические особенности устойчивости экономических систем Последние десятилетия характеризуется интенсивной разработки так называемой теории экономического равновесия, которое стало одним из важнейшим разделом математической экономики. Одним из вопросов исследуемых в теории равновесия является проблема создания таких условий, при которых предложения товаров полностью удовлетворяло бы спрос на них. При чем производители и потребители товара не были бы заинтересованы в изменении сложившейся ситуации и не стремились бы к нарушению сложившегося состояния равновесия. Устойчивой равновесной экономической системы, равновесия которых поддерживается рыночным процессом регулирования цен, является типичным примером экономического гомеостазиса. 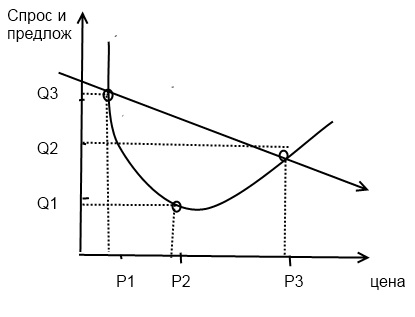 4. Моделирование Моделирование – основной метод кибернетики Роль аналогии и моделирования как методов научного познания Анализ процессов протекающих в сложных кибернетических системах сопряжен со значительными трудностями. В тоже время не редко бывает так, что те или иные свойства и характеристики трудно обнаружит в какой-либо системе, в процессе или явлении, но сравнительно заметно их можно обнаружить в другой системе, в процессе или явлении, которые схожи с первым по определенным признакам. Это дает возможность использование в процессе познания методов аналогии и моделирования. По сути дела, в любых отраслях знания при объяснения сложных явлений, мы ищем сходства, аналогии с тем, что нам уже известно. Таким образом, мы стремимся к объяснению неизвестного, не понятного через известное и понятное. Аналогию определяют как сходство или подобие в определенном отношении между различными предметами или явлениями. В известных границах аналогия может служить средством познания нераскрытых ещё признаков и свойств исследуемых объектов или процессов. Получение того или иного вывода с помощью метода аналогии можно пояснить следующим образом: пусть некоторые объекты А и В, характеризуется одинаковыми свойствами a, b, c, d, e. Пусть далее у объекта А наблюдается свойство f. Пользуясь методом аналогии можно предполагать, что и объект В так же обладает этим, хотя и не наблюдаемым непосредственно свойством f. Например, наблюдая процессы пищеварения у человека и у ряда животных, и отмечая наличие многих соблюдающих свойств можно сделать, что и другие свойства у них являются общие. Это позволяет ставить на животных те или иные опыты, исследовать на них влияние новых фармакологических средств, отрабатывать технику хирургических операций и затем по аналогии использовать полученные данные для лечения человека. Объективное основание для такого логического переноса признаков с одного известного нам объекта на другой неизвестный объект базируется на том факте, что свойство любой системы существует, не изолировано одно от другого, а тесно взаимосвязаны, при чем изменения любого существенного признака, как правило, сказывается и на других признаков. Это дает основание предполагать, что если 2 объекта наблюдения обладают одинаковой совокупностью определенных свойств и если один из объектов обладает ещё некоторым свойством (закономерно связанной с данной совокупностью свойств), то и другой объект должен обладать этим же свойством. Однако, делая выводы или умозаключения, на основе аналогии нужно отчетливо представлять, что эти выводы не являются абсолютно достоверными, истинными, а носит лишь более и менее вероятностный характер, и поэтому всегда нуждается дополнительной проверки. Так, например, сравнивая структуру мозга человека и высших животных, электрохимические процессы, происходящие в их нервных клетках, механизмы условных рефлексов можно прийти совершенно к неверному выводу, а способностей к животных к абстрактному мышлению, возможности овладению ими математическим аппаратом и т.п. Поэтому, пользуясь методом аналогии очень важно изучать не только сходные свойства объекта, но и отличительные, оценивать существенность тех или иных, логически осмысливать их возможное влияние на новое прогнозированное свойство исследуемого объекта. Исключительно важную роль в исследовании кибернетических систем играет метод моделирования. Моделирование имеет весьма большое сходство с методом аналогии, так что его можно рассматривать как разновидность или дальнейшее развития метода аналогии. Модель представляет искусственный созданный человеком объект любой природы (умозрительный или материально реализованный), который замещает или воспроизводит исследуемый объект так, что ее изучение способна дать новую информацию об этом объекте. Моделирование как метод познания основан на способности человека абстрагировать сходные признаки или свойства у различных объектов и устанавливать между ними определенные соответствия. Благодаря этому появляется возможность исследовать некоторые свойства объектов не непосредственно, а опосредовано через изучения других более доступных исследуемых моделей этих объектов сходных с объектами оригиналами. Основные виды моделей При подробно детализированной классификации различают более 10 классов и подклассов моделей. Однако, достаточно четкое представление о главных отличительных чертах моделей дает разделение на 4 основные вида: - геометрические - физические - предметно-математические - логико-математические Геометрические модели представляет некоторый объект геометрически подобный к своему прототипу (оригиналу). Геометрические модели дают внешнее представление об оригинале и большей части служат для демонстрационных целей. К этому виду моделей можно отнести слепки, выполненные в натуральную величину из того же материала, что и оригинал или с другого материала (копия скульптуры, демонстрационная модель детали машины, муляжи плодов и т.п.). Чаще, однако, модели выполняются в другом масштабе (макет здания, модель корабля, рельефная карта местности), а в реале случаев и с изменением мерности пространства, а именно 2ух мерная плоская карта в 3ьох мерной местности, 2ух мерный чертеж 3ьох мерных деталей и т.п. В основе построения геометрических моделей без изменения мерности пространства лежит определение подобие геометрических объектов, которое гласит, что 2 геометрических объекта считаются подобными, если при соответствующим взаимном расположении можно добиться их совпадения при однородной деформации линейных размеров, то есть при изменения размеров в одно и тоже число раз. По сколько при построении геометрических моделей основную роль играет их геометрическое подобие, а не процессы функционирования, то кибернетики, изучающие процессы управления, эти модели могут иметь лишь подсобное значение (вспомогательное). Физические модели отражает подобие между оригиналом и моделью не только с точки зрения их формы и геометрических соотношений, но и с точки зрения происходящих в них основных физических процессов. Физически подобными называются явления геометрически подобные системам, при которых в процессе их функционирования, отношения характеризующих их одноименных физических величин в сходных точках являются постоянной величиной. При физическом моделировании модель и её прототип всегда является объектами, имеющие одинаковую физическую природу. Примерами использования методов физического моделирования являются: 1) определение аэродинамических свойств летательных аппаратов, путем «продувки» их моделей в аэродинамической трубе 2) исследования предполагаемого поведения гидротехнических сооружения (платин, дамб, шлюзов и т.п.) путем натуральных испытаний аналогичных объектов значительно меньших размеров 3) исследования на моделях особенности работы атомных реакторов, радиопередающих антенн, линий электропередач и т.п. При этом всегда изменяются не только геометрические размеры моделей, но и соответственно другие физические параметры. Так при построении модели платины в 1/10 натуральной величины в 10 раз уменьшается и давление на нее воды. При моделировании радиопередающей антенны соответственно изменяется длина волны, напряжение, сила тока и т.п. Предметно-математические модели. Еще более широкие возможности моделирование сложных процессов и явлений открываются при использовании метода предметно-математического моделирования, рассматриваемого иногда как разновидность физического моделирования, при котором снимается требование тождественности физического природы оригинала и его модели. Этот метод предполагает лишь тождественность математического описания процессов в оригинале и модели, хотя эти процессы и могут развиваться на совершенно отличной материальной основе. В таком определении предметно-математическая модель представляет материальную систему, в которой происходят иные физические процессы, чем в оригинале, но и те и другие могут быть описаны одинаковыми или подобными математическими выражениями. Модели, которые могут быть построены на основе непосредственной связи (аналогии) между величинами, характеризующие физически различные явления относят к предметно-математическим моделям прямой аналогии. Моделирование при этом осуществляется реальными вещественными системами, явлением которых описываются одними и теми же уравнениями и следовательно в определенном отношении эти явления изоморфны друг к другу. В отличие от них, к предметно-математическим моделям непрямой аналогии относят различные типы вычислительных машин. По характеру представления величин (машинных переменных) все средства вычислительной техники делятся на 2 основных класса: - аналоговые машины - цифровые вычислительные машины Логико-математические модели. Под логико-математическими моделями, которые называют так же формальными, математическими, логическими моделями понимают абстрактные описания объектов с помощью знаков. Таким образом, логико-математическая модель, которую далее мы будем называть математической моделью, представляет некоторую совокупность уравнений или неравенств, таблицы, матрицы и другие способы математического описания тех или иных явлений и процессов. Следовательно, такая модель фиксируется особой математической структурой отражающей свойства объекта, проявляемым им конкретным условием его существования, движения и развития. К математическим моделям относят модели математической физики, квантовой механики, структурной лингвистики и т.п. Важным классом этих моделей являются экономико-математические модели различных модификаций. Понятие о «черном ящике» При постановки и решении задач моделирование сложных систем удобно пользоваться понятием «черного ящика». Черным ящиком называют систему, внутреннее содержание которое наблюдателю неизвестно, а доступными ему являются только входы и выходы в систему. 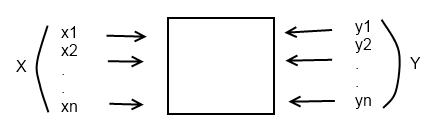 Если осуществлять достаточно длинный эксперимент, который будет заключаться в реализации различных наборов входных воздействий x1, x2…xn и наблюдений, имеющих место при этих реакций у1,у2..уn. И далее сопоставить и проанализировать результаты этого эксперимента, то не смотря на незнание внутренней структуры наблюдаемой системы, можно составить более или менее правильное представление по её поведении в разных условиях. Это дает возможность путем экстраполяции осуществлять и относительно давать достоверное предсказание поведения системы в непроверенных условиях. Метод черного ящика хорошо используется на практике в различных ситуациях. Во-первых, нас может совершенно не интересовать внутренняя структура системы, а важным является только её поведение. Например, телезритель, как правило, пока телевизор исправим не интересуется его схемой и взаимодействия его элементов, то есть телевизор является для телезрителя черным ящиком, о роботе которого он судит по входным воздействиям (включение питание, изменение положением регулятора яркости, громкости звука и т.п.) и соответствующим реакциям данного черного ящика (качества звука и изображения) |
