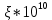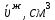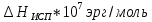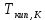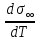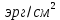Размерная зависимость поверхностного натяжения наночастицы, находящейся в собственной матрице в изобарических условиях. 3. ОСНОВА. Нанотехнологии
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
Глава 2. Зависимость поверхностного натяжения наночастицы, находящийся в матрице в изобарических условиях 2.1. Дифференциальное уравнение для зависимости поверхностного натяжения от размера при условиях постоянного давления в матрице В литературе наибольшее внимание уделяется установлению зависимости поверхностного натяжения от размера в изотермических условиях. Между тем, с изменением размера дисперсной частицы (фаза α), находящейся в дисперсионной среде (фаза β) в равновесных условиях (например, жидкая капля в собственном насыщенном паре) меняются значения основных параметров состояния системы (в однокомпонентной системе температура равновесия Т и давления в сосуществующих фазах Р(α) и Р(β)). При этом во многих случаях вызывает интерес, в частности, влияние кривизны поверхности на температуру равновесия фаз. Для однокомпонентной системы жидкость-пар влияние размера на давление в жидкой фазе Р(α) (r) выражена во много раз сильнее, чем для пара Р(β). В качестве разделяющей поверхности выберем в пределах переходного слоя между фазами поверхность натяжения, положение которой определяется условием 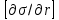 =0. Поверхностное натяжение равно работе образования единицы поверхности, где справедливо соотношение [20] =0. Поверхностное натяжение равно работе образования единицы поверхности, где справедливо соотношение [20]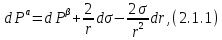 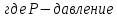 Пользуясь условиями 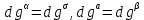 и выражениями для полных дифференциалов dg и получаем и выражениями для полных дифференциалов dg и получаем 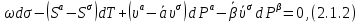 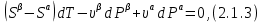 где S, 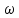 , , 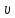 – энтропия, поверхность и объем, приходящаяся на один моль. – энтропия, поверхность и объем, приходящаяся на один моль.Зафиксируем давление в паровой фазе ( 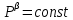 ) при нахождении зависимости поверхностного натяжения ) при нахождении зависимости поверхностного натяжения 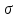 от радиуса кривизны r от радиуса кривизны rРассмотрим влияние размера на поверхностное натяжение дисперсной частицы сферической формы в жидком состоянии, находящейся в паровой фазе в жидком состоянии, находящейся в паровой фазе макроскопического размера при условии постоянства давления в паре (Р(β)=const). При этом будем учитывать влияние размера дисперсной частицы на температуру равновесия в системе. 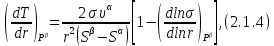 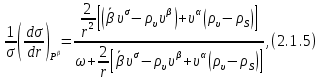 где r – радиус поверхности натяжения, 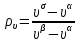 , , 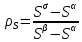 В случае сферической формы наночастицы безразмерную величину 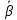 можно выразить через параметр Толмена можно выразить через параметр Толмена 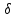 в виде в виде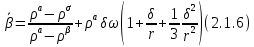 где 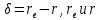 радиусы эквимолекулярной разделяющей поверхности и поверхности натяжения соответственно радиусы эквимолекулярной разделяющей поверхности и поверхности натяжения соответственноПри интегрировании уравнения ГТКБ обычно принимается не зависимость параметра Толмена от радиуса (при этом сохраняется зависимость от температуры) и для него используется значение 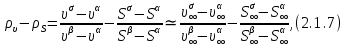 где величина с индексом « 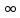 » относится к микроскопическому размеру. » относится к микроскопическому размеру. Для границы жидкость-пар, где 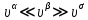 имеем имеем 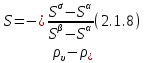 Из теории поверхностных явлений в макроскопических системах известно выражение 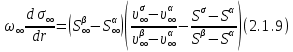 Видно, что разность 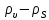 с использованием (2.1.7) и (2.1.9) можно записать в виде с использованием (2.1.7) и (2.1.9) можно записать в виде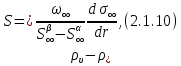 где 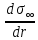 – температурный коэффициент поверхностного натяжения на плоской поверхности (r= – температурный коэффициент поверхностного натяжения на плоской поверхности (r=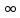 ). ).Уравнение (2.1.5) является аналогом уравнения Гиббса-Толмена-Кенига-Баффа, которое справедливо в изотермических условиях. С использованием условия (2.1.5) можно привести к виду 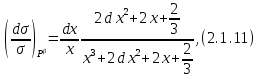 где 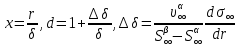 Представим это соотношение в виде 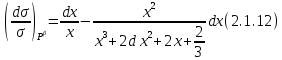 2.2. Размерная зависимость поверхностного натяжения сферической частицы произвольного размера в изобарических условиях Интегрирование (2 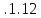 ) на всем интервале размеров позволяет получить следующее уравнение для размерной зависимости поверхностного натяжения в изобарических условиях ) на всем интервале размеров позволяет получить следующее уравнение для размерной зависимости поверхностного натяжения в изобарических условиях 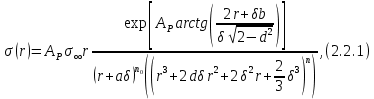 где 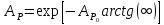 , , 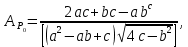 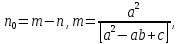 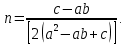 Величины a, b, c связаны с соотношениями a+b=2d, c+ab=2, ac=2/3. При этом величина a, b и c связаны соотношением a+b=2d, c+ab=2, ac=2/3. Общий анализ уравнения (2.2.1) показывает, что вся зависимость 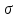 от r при от r при 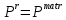 зависит от знака и численного значения величины d. При этом возможны случаи увеличения и уменьшения поверхностного натяжения от размера. При зависит от знака и численного значения величины d. При этом возможны случаи увеличения и уменьшения поверхностного натяжения от размера. При 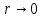 поверхностное натяжение также стремится к нулю. Величина d в (2 поверхностное натяжение также стремится к нулю. Величина d в (2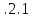 ), в общем случае, может иметь любой знак. Для случая, когда рассматривается жидкая нанокапля, находящаяся в собственном паре в равновесном состоянии, величина ), в общем случае, может иметь любой знак. Для случая, когда рассматривается жидкая нанокапля, находящаяся в собственном паре в равновесном состоянии, величина 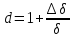 может иметь отрицательный знак. Это связано с тем, что для жидкостей на границе с паром при температурах, далеких от критической температуры‚ может иметь отрицательный знак. Это связано с тем, что для жидкостей на границе с паром при температурах, далеких от критической температуры‚ 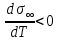 что может привести к неравенству что может привести к неравенству 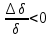 Об этом свидетельствуют данные наших расчетов, приведенные в таблице 3. При этом для Об этом свидетельствуют данные наших расчетов, приведенные в таблице 3. При этом для 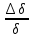 использовано соотношения использовано соотношения 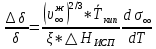 , которое следует из определения , которое следует из определения 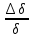 с учетом соотношения с учетом соотношения 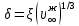 ,где ,где 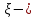 коэффициент, зависящий от структуры предплавления. коэффициент, зависящий от структуры предплавления. Таблица 3 Значения 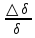 и d для жидких металлов при температуре плавления и входные данные для их расчета и d для жидких металлов при температуре плавления и входные данные для их расчета
2.3. Размерная зависимость поверхностного натяжения больших и предельно малых частиц в изобарических условиях Рассмотрим ряд частных случаев, относящихся к разным размерам дисперсной частицы. Квазиплоская поверхность (очень малая кривизна или очень большой радиус кривизны). В таком случае можно принять условие 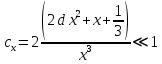 и из ( и из (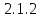 ) будем иметь ) будем иметь 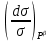 =0, =0, 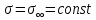 . В такой области размерный эффект поверхностного натяжения отсутствует. . В такой области размерный эффект поверхностного натяжения отсутствует.Область, где можно принять условие 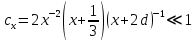 Из (2  ) следует в этом случае ) следует в этом случае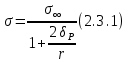 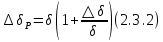 Область, где имеет место неравенство 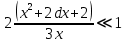 Зависимость от размера поверхностного натяжения дисперсной частицы, находящейся равновесии с собственным насыщенным паром в этом случае, как следует их (  ), описывается выражением ), описывается выражением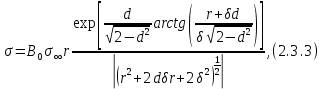 где 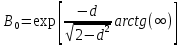 При малых размерах дисперсной частицы, когда выполняется условие 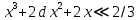 В этом случае имеет из (  ) )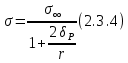 Область очень больших искривлений поверхности (очень малых частиц), где второе слагаемое в правой части (  ) равно нулю. ) равно нулю.В этой области имеем  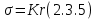 где, K= 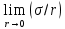 – коэффициент, зависящий от температуры в случае однокомпонентной системы. – коэффициент, зависящий от температуры в случае однокомпонентной системы.Из (2.3.5) можно сделать заключение о том, что линейная зависимость поверхностного натяжения от радиуса поверхности натяжения имеет место и в случае постоянства давления в матрице. 2.4. Результаты численных расчетов по зависимости 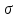 от r при P=const от r при P=constУравнение для зависимости 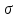 на границе с паром от радиуса на границе с паром от радиуса 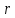 поверхности натяжения в однокомпонентной системе при условии постоянства давления в паре ( поверхности натяжения в однокомпонентной системе при условии постоянства давления в паре (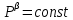 ) отличается от аналогичного уравнения при условии постоянства температуры. ) отличается от аналогичного уравнения при условии постоянства температуры. Нами подобраны наиболее надежные данные для проведения численных расчетов по зависимости поверхностного натяжения от размера в изобарических условиях. Они приведены в таблицу 3. Структурный параметр 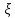 зависит от типа структуры плавления и имеет значения 0,64*10-9 и 0,70*10-9 для ОЧК и ГЦК структур, соответственно. Остальные величины являются структурными данными. Молярным объем зависит от типа структуры плавления и имеет значения 0,64*10-9 и 0,70*10-9 для ОЧК и ГЦК структур, соответственно. Остальные величины являются структурными данными. Молярным объем 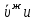 температурных коэффициент относится к температуре плавления. Из этих данных следует, что безразмерные величины температурных коэффициент относится к температуре плавления. Из этих данных следует, что безразмерные величины 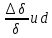 имеют отрицательные знаки для плоской границы жидкий металл-пар. При этом нет корреляции численных значений этих величин от одной из величин, включенных в эту таблицу. Численные значения имеют отрицательные знаки для плоской границы жидкий металл-пар. При этом нет корреляции численных значений этих величин от одной из величин, включенных в эту таблицу. Численные значения 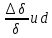 определяются в целом комбинацией всех других величин, включенных в таблицу 3. определяются в целом комбинацией всех других величин, включенных в таблицу 3. Зависимость 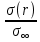 от от 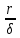 при постоянстве давления в паровой фазе, в которой находится дисперсная частица в равновесном состоянии, приведено на рисунке 8. Расчеты при d>0 приводят к монотонной зависимости поверхностного натяжения от размера дисперсной частицы (кривые 1, 2 на рисунке 4). при постоянстве давления в паровой фазе, в которой находится дисперсная частица в равновесном состоянии, приведено на рисунке 8. Расчеты при d>0 приводят к монотонной зависимости поверхностного натяжения от размера дисперсной частицы (кривые 1, 2 на рисунке 4).При значениях d<0 имеет место возрастание поверхностного натяжения в области больших радиусов поверхности натяжения и уменьшение в области малых радиусов. Это приводит к тому, что на кривой, описывающей зависимость 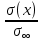 от от 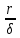 , имеется максимум (рис.4‚ кривые 3 и 4). , имеется максимум (рис.4‚ кривые 3 и 4). При отрицательных значениях d, больших по модулю d*=1,5533 решение дифференциального уравнения 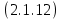 в виде (2 в виде (2 ) теряет силу. Наши расчеты показывают, что для жидких металлов значение d находятся в интервале от 0 до d* (таблица 3), что приводит к появлению разрыва на зависимости поверхностного натяжения от радиуса поверхности натяжения. ) теряет силу. Наши расчеты показывают, что для жидких металлов значение d находятся в интервале от 0 до d* (таблица 3), что приводит к появлению разрыва на зависимости поверхностного натяжения от радиуса поверхности натяжения. В изотермических условиях имело место монотонное уменьшение поверхностного натяжения жидких нанокапель металлов с уменьшением радиуса поверхности натяжения. 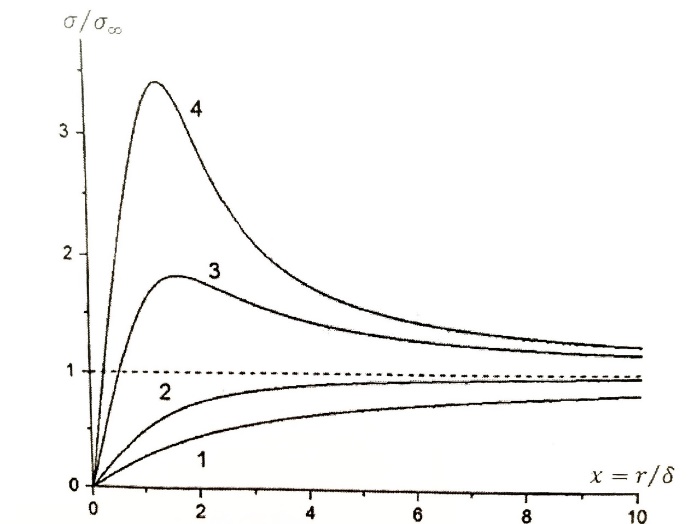 Рис. 4. Размерная зависимость поверхностного натяжения наночастицы сферической формы на границе с насыщенным паром при различных значениях параметра d (1- d=1; 2- d=0,1; 3- d=-0,75; 4- d=-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||