Размерная зависимость поверхностного натяжения наночастицы, находящейся в собственной матрице в изобарических условиях. 3. ОСНОВА. Нанотехнологии
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
2.5. Выводы к главе 2 1. Получено соотношение по размерной зависимости поверхностного натяжения наночастицы сферической формы, находящиеся в матрице макроскопического размера в однокомпонентной системе, при условии постоянства давления в матрице (Pmatr=const); 2. Из анализа размернозависимого уравнения изобары поверхностного натяжения, полученного в работе, следует возможность существования качественно различных зависимостей поверхностного натяжения 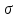 от размера r в том числе: от размера r в том числе:Монотонное изменение; Прохождение через максимум; Наличие полюса (разрыва на зависимости 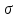 от r). от r).3. Монотонное уменьшение поверхностного натяжения при переходе к более малым размерам характерно для твердой наночастицы, находящиеся в жидкости 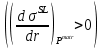 ; ;4. Для жидкой нанокапли сферической формы, находящиеся собственном паре, с уменьшением ее размера, имеет место возрастание поверхностного нахождения в области больших размеров частицы 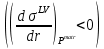 , уменьшение в области малых размеров частицы , уменьшение в области малых размеров частицы 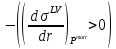 и характеризуется, таким образом, наличием максимума поверхностного натяжения в области средних размеров наночастицы и характеризуется, таким образом, наличием максимума поверхностного натяжения в области средних размеров наночастицы 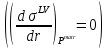 ; ;5. Наличие разрыва на границе зависимости поверхностного натяжения от радиуса сферической формы, находящиеся в собственном паре 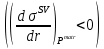 , ,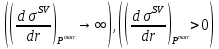 является следствием больших численных значений температурного коэффициента поверхностного натяжения по модулю, которое является отрицательной величиной. является следствием больших численных значений температурного коэффициента поверхностного натяжения по модулю, которое является отрицательной величиной.Общие выводы Получено новое дифференциальное уравнения по размерной зависимости поверхностного натяжения наночастицы сферической формы, находящиеся в матрице, при условии постоянства давления в матрице (Pmatr=const), которая является аналогом дифференциального уравнения Гиббса-Толмена-Кёнига-Баффа, в условиях постоянства температуры (T=const). Предельные значения размерного параметра 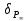 при условии Pmatr=const может отличаться от параметра Толмена по знаку и абсолютному значению при условии Pmatr=const может отличаться от параметра Толмена по знаку и абсолютному значению 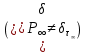 . .Найдено новое уравнение по размерной зависимости поверхностного натяжения сферической наночастицы, находящиеся в дисперсионной среде при условии (Pmatr=const) в интегральной форме. Показано, что для жидких металлов 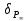 имеет отрицательный знак и по абсолютной величине превышает значения параметра Толмена. имеет отрицательный знак и по абсолютной величине превышает значения параметра Толмена.Рассчитана размерная поверхностного натяжения наночастицы на границе с матрицей в безразмерных координатах 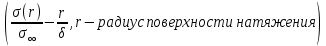 при разных значениях величины d. при разных значениях величины d.Численные расчеты показывают, что с уменьшением размера наночастицы при d>0 поверхностное натяжение монотонно уменьшается и при d<0 возрастает, проходит через максимум и затем уменьшается. Из полученных результатов видно, что для жидких и твердых наночастиц, находящихся в собственном паре, характерна немонотонная зависимость поверхностного натяжения от размера. Для твердой наночастицы, находящейся в собственном расплаве, наиболее вероятно монотонное уменьшение поверхностного натяжения при переходе к более малым размерам наночастицы. Литература 1. Гусев, А.И. Нанокристаллические материалы, методы получения и свойства / А.И. Гусев. – Екатеринбург: ИХТТ УрОРАН, 1988. – 199 c 2. Metal nanoparticles: Synthesis, characterization and applications / Ed. by. D.L. Feldheim, C.A. Foss (Jr). – New York - Basel: Marcel Dekker Inc., 2002. – 352 p. 3. Петров, Ю.И. Кластеры и малые частицы / Ю.И. Петров. – М.: Наука, 1986. – 361 4. Петров, Ю.И. Физика малых частиц / Ю.И. Петров. – М.: Наука, 1982. – 359 c. 5. Непийко, С.А. Физические свойства малых металлических частиц / С.А. Непийко. – Киев: Наукова думка, 1985. – 246 с. 6. Ролдугин, В.И. Квантоворазмерные металлические коллоидные системы / В.И. Ролдугин // Успехи химии. – 2000. – T. 69. – № 10. – C. 899-923 7. Sergeev, G.B. Encapsulation of small metal particles in solid organic matrices: Review Article / G.B. Sergeev, M.A. Petrukhina // Progress in Solid State Chemistry. – 1996. – V. 24. – I. 4. – P. 183-211. 8. Помогайло, А.Д. Полимер - иммобилизированные наноразмерные и кластерные частицы металлов / А.Д. Помогайло // Успехи химии. – 1997. – Т. 66. – № 8. – С. 750-791 9. Хайрутдинов, Р.Ф. Химия полупроводниковых наночастиц / Р.Ф. Хайрутдинов // Успехи химии. – 1998. – Т. 67. – № 2. – С. 125-139. 10. Р. А. Андриевский ОСНОВЫ НАНОСТРУКТУРНОГО МАТЕРИАЛОВЕДЕНИЯ ВОЗМОЖНОСТИ И ПРОБЛЕМЫ // Москва Лаборатория знаний 2017, ст. 6-12 11. Андриевский Р.А., Рагуля А.В. Наноструктурированные материалы. М.: Издательский центр „Академия“, 2005. 192 c 12. Гиббс Дж.В. Термодинамика. Статистическая механика. — М.: Наука, 1982. — 582 с. 13. Ван-дер-Ваальс И.Д., Констамм Ф. Курс термостатики. T.1. — ОНТИ, 1936. — 318 с. 14. Van der Waals I.D. Thermodynamische Theorie der Capil-laritat. — Verh. Kon. Acаd. — Amsterdam, 1893. 15. Guggenheim В.A. Thermodynamics. — Amsterdam: North-Holland Publishing Co., 1967. 16. Русанов А.И. Фазовые равновесия и поверхностные явления. — Л.: Химия, 1967. — 388 с. 17. Rusanov A.I. Phasengleichgewichte und Oberflachener-scheinungen. — Berlin: Academie-Verlag, 1978. — 678 s. 18. Ю. К. Машков, о. В. Малий «Материалы и методы нанотехнологии», Омск Издательство ОмГТУ 2014 19. Ахметов М. А. Введение в нанотехнологии //Образовательный центр «Участие». - 2012. - C. 108. 20. Сергеев Г. Б. Размерные эффекты в нанохимии// Рос. хим. ж. (Ж. Рос. хим. об-ва им. Д. И. Менделеева), - 2002. - т. XLVI. - №. 5. 21. Гусев А.И. Наноматериалы, наноструктуры, нанотехнологии//Физматлит, - 2007. -- C.416. 22. Likharev, K.K. Single Electronics K.K. Likharev, T. Claeson // Sci. Amer. –1992. №6. – P. 50–55. 23. С позиции квантовой механики электрон представлен волной, описываемой соответствующей волновой функцией. Распространение этой волны в наноразмерных твердотельных структурах контролируется эффектами, связанными с квантовым ограничением, интерференцией и возможностью туннелирования через потенциальные барьеры 24. Ч. Пул-мл., Ф. Оуэнс. Нанатехнологии. /Пер. с англ. Под ред. Ю. И. Головина. М.: Техносфера, 2006, 336 с 25. Р.Р. Мулюков. Развитие принципов получения и исследования объемных наноструктурных материалов в ИПСМ РАН. // Российские нанотехнологии, 2007, Т. 2, № 7-8, с.38-53. 26. Драгунов В.П., Неизвестный И.Г., Гридчин В.А. Основы наноэлектроники Учебное пособие// Логос. - 2006. -- М. -- C. 496. 27. Шебзухов Заур Азмет-гериевич Размерная зависимость поверхностного натяжения и поверхностной энергии металлических наночастиц на границах жидкость–пар и твѐрдое–жидкость // Нальчик – 2014 ст. 21-24 28. . Tolman, R.C. The effect of droplet size on surface tension / R.C. Tolman // Journal of Chemical Physics. – 1949. – V. 17. – P. 333-337. 29. Русанов, А.И. Термодинамика поверхностных явлений / А.И. Русанов. ЛГУ, 1960. – 179 с. 30. . Русанов, А.И. Зависимость поверхностного натяжения от кривизны поверхности / А.И. Русанов // Сборник трудов XIV Международной конференции по химической термодинамике, НИИ Химии СПбГУ. – 2002. – С. 349-350. 31. Шебзухов, З.А. Межфазное натяжение и параметр Русанова на сильно ис- 187 кривленных поверхностях с различным характером кривизны / З.А. Шебзухов, М.А. Шебзухова, А.А. Шебзухов // Известия РАН. Серия физическая. – 2009. – Т. 73. – № 7. – С. 983-986. |
