реферат. Например, если при делении многочлена

• Название: Например, если при делении многочлена
• Дата: 27.10.2022
• Размер: 105.65 Kb.
• Имя файла: реферат.docx
• Тип: Документы; #758070

Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:



Например, разделим многочлен 2x³ − 2x² − 5x + 4 на многочлен x − 3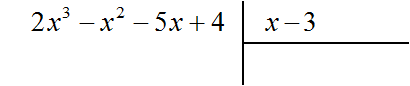



Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x². Записываем 2x² в частном: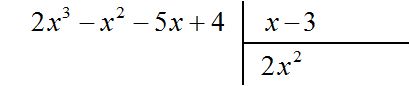



Умножим 2x² на делитель x − 3 и полученный результат запишем под делимым: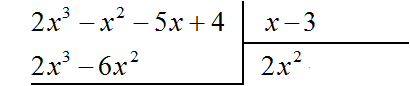



Вычтем из делимого полученный многочлен 2x³ − 6x²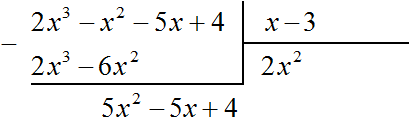



Теперь делим 5x² − 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном: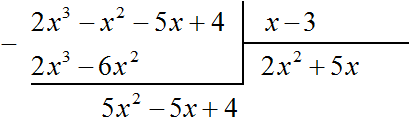



Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x² − 5x + 4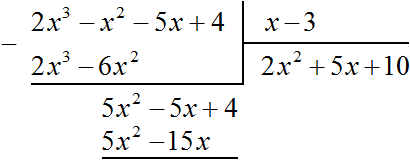



Вычтем из многочлена 5x² − 5x + 4 многочлен 5x² − 15x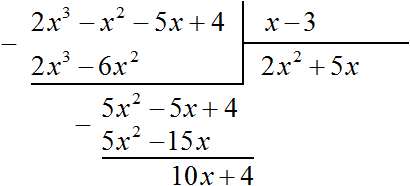



Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном: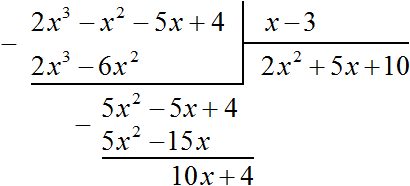



Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4. Сразу вычтем этот полученный результат из делимого 10x + 4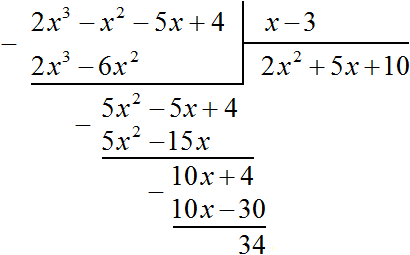



Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4, является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34.

Поэтому при делении многочлена 2x³ − 2x² − 5x + 4 на многочлен x − 3 получается 2x² + 5x + 10 и 34 в остатке.

Государственное автономное профессиональное образовательное учреждение

«Казанский нефтехимический колледж имени В.П. Лушников

РЕФЕРАТ

Деление многочленов с остатком.

Алгоритм Евклида.


Выполнила:

Лавонина Юлия

группы 3903

Преподаватель:

Кадырова Н.И

Казань

2019

Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:



Давайте разберемся, что означает понятие «наибольший общий делитель».

Попробуем объяснить в не строгой форме.

Допустим у нас есть два числа, у этих двух чисел есть число, на которое они оба делятся. Максимально большое такое число и есть наибольшим общим делителем. Т.е. наибольший общий делитель – наибольшее число, на которое можно разделить несколько чисел без остатка. Строгое определение мы рассмотрим чуть позже.

Наибольший общий делитель(НОД)двух и более натуральных чисел – это наибольшее из натуральных чисел, на которое делится каждое из данных чисел.

Есть два числа  ,   их наибольший делитель будет записан так:

.

Например,  .

Числа в скобках написаны через точку с запятой, чтобы не путать числа с десятичной дробью.

Существует еще такая форма записи НОД:



Свойства НОД:

Давайте подумаем в каких границах может находиться НОД двух чисел.

Первое свойство.

У любых двух чисел есть хотя бы один общий делитель, и это число 1.

И здесь мы введем понятие взаимно простых чисел.

Два числа называются взаимно простыми, если их наибольший общий делитель равен единице.

Что это значит? Это значит, что на самом деле у них нет других общих делителей, кроме единицы. Какие примеры взаимно простых чисел мы можем привести?

Например, числа 2 и 3, которые мы рассматривали выше. Числа 3 и 7 также взаимно простые.

Очень важно не путать понятия взаимно простых чисел, и простых чисел.

Из того что числа взаимно простые еще не следует, что они простые.

Например,  . Тем не менее ни 9, ни 10 не являются простыми числами, но они взаимно простые.

Второе свойство.

Как вы думаете, если даны два числа   и  , причем   нацело делится на   ( ), чему тогда равен  ?

 – такое наибольшее число, на которое делятся и  , и  . Логично, что наибольшее число, на которое делится   –  , а   – по условию.

Значит,  .

Например,  ;

Аналогично  ;

, потому что   и больше 1 результат быть не может

Алгоритм Евклида:

Найдем  .

Идея алгоритма в следующем: заменяем большее из чисел их разностью.

 при этом НОД не меняется.

Алгоритм Евклида с вычитанием заключается в последовательной замене наибольшего числа из двух данных чисел, для которых вычисляется НОД, разностью этих чисел.

Продолжим


Можно продолжать и дальше, но тут ответ уже очевиден

, т.к.  .

Ответ  11.

Мы можем использовать этот алгоритм и для тех чисел, которые мы уже разобрали.

, т.к. 

К сожалению, для трех чисел этот алгоритм настолько легко не работает. С другой стороны, у этого алгоритма есть несколько улучшений, есть алгоритм Евклида не с вычитанием, а с делением, поэтому если вам интересно, обязательно спросите у своего учителя, в чем он заключается и возможно вы сами сможете использовать этот более сильный метод.

Давайте не углубляясь разберемся, откуда же берется сама идея алгоритма с вычитанием. Наверняка вы знаете свойство делимости, что если два числа делятся на третье, то и сумма или разность двух чисел также делится на это третье, если   и  , то  . Это свойство мы здесь и используем.