ПО ДЛЯ АВТОМАТИЗИРОВАННОГО ФОРМИРОВАНИЯ МОДЕЛЕЙ КИНЕМАТИКИ. Научно-исследовательская работа. Научноисследовательская работа Оглавление
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ДЛЯ АВТОМАТИЗИРОВАННОГО ФОРМИРОВАНИЯ МОДЕЛЕЙ КИНЕМАТИКИ ОТКРЫТЫХ КИНЕМАТИЧЕСКИХ ЦЕПЕЙ МЕХАНИЗМОВ Научно-исследовательская работа ОглавлениеВведениеОдной из характеристик современного производства является широкое применение автоматических и автоматизированных систем управления. Автоматизация основной части технологического процесса оставляет человеку выполнение лишь несложных, но однообразно повторяющихся утомительных вспомогательных ручных операций. Очевидно, что для решения проблемы комплексной автоматизации производства нужно создание принципиально новых машин, имитирующих действия человека в трудовых процессах. Именно промышленные роботы являются таким классом производственных машин. Исполнительными устройствами в них стали многозвенные манипуляторы с управляемыми приводами по каждой степени подвижности. Автоматизация сложных ручных операций с помощью серийно выпускаемых промышленных роботов практически невозможна. Поэтому необходима разработка специальных промышленных роботов применительно к узкому классу технологических операций. Таким образом, в процессе разработки отличающихся по конструктивному исполнению моделей манипуляторов возникает необходимость формализованного способа описания их кинематических цепей, позволяющего компактно и полно отображать всю необходимую совокупность данных о структурах и параметрах описываемого механизма. Подобный способ описания должен быть удобным для решения всей совокупности задач, связанных с формированием банков данных о манипуляторах, их структурным и кинематическим анализом на ЭВМ. В данной работе, на основе ранее предложенного в [1] способа формализованного описания кинематических цепей манипуляционных механизмов разработано алгоритмическое и программное обеспечение для автоматизированного формирования моделей кинематики открытых кинематических цепей описываемых механизмов. 1. Формализованное описание кинематических цепей механизмовРазработанный способ описания структур и параметров кинематических цепей манипуляторов основан на формализованном описании всех входящих в цепь звеньев и сочленений. При этом каждый элемент описывается соответствующим его типу идентификатором и набором параметров, часть из которых отражает структурные связи в кинематической цепи, а остальные определяют собственные параметры этого звена или сочленения. Описание каждого элемента имеет структуру 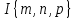 . Здесь . Здесь 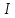 – идентификатор описываемого элемента; – идентификатор описываемого элемента; 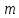 — собственный номер данного элемента, присвоенный в процессе описания цепи; — собственный номер данного элемента, присвоенный в процессе описания цепи; 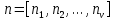 – вектор собственных номеров элементов цепи, с которыми непосредственно связан элемент m; – вектор собственных номеров элементов цепи, с которыми непосредственно связан элемент m; 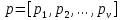 – вектор конструктивных параметров элемента m, определяющих его геометрию и положение относительно других элементов. Параметры – вектор конструктивных параметров элемента m, определяющих его геометрию и положение относительно других элементов. Параметры 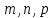 являются позиционными, т. е. последовательность их записи строго определена. являются позиционными, т. е. последовательность их записи строго определена.Ниже представлены наборы конструктивных параметров для основных элементов кинематических цепей (звеньев и одноподвижных сочленений) [1]. 1. Сочленения. Идентификаторы сочленений начинаются с символа 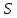 (сочленение). Их структура имеет вид (сочленение). Их структура имеет вид 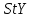 , где , где 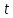 – число степеней относительной подвижности звеньев кинематической пары, образуемой данным сочленением; – число степеней относительной подвижности звеньев кинематической пары, образуемой данным сочленением; 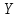 – символ, указывающий на тип сочленения. На позиции – символ, указывающий на тип сочленения. На позиции 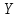 в предлагается использовать: в предлагается использовать: 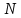 – для жесткого соединения; – для жесткого соединения;  – для вращательной кинематической пары 5-го класса; – для вращательной кинематической пары 5-го класса;  – для поступательной кинематической пары 5-го класса; – для поступательной кинематической пары 5-го класса; 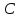 – для сочленения сферического типа 3-го класса; – для сочленения сферического типа 3-го класса; 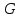 – для сочленения типа шарнира Гука; – для сочленения типа шарнира Гука; 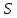 – для сочленение сферического типа 3-го класса. – для сочленение сферического типа 3-го класса.1.1. Неподвижное сочленение. Для него формализованное описание имеет вид 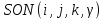 . .1.2. Сочленение вращательного типа 5-го класса. Для этого типа сочленений формализованное описание имеет вид 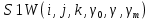 . .1.3. Сочленение поступательного типа 5-го класса. Отличительная особенность кинематических пар с сочленениями данного типа – изменение длины оси одного из звеньев кинематической пары при их относительном смещении. Таким образом, формализованное описание для данного сочленения принимает вид  . .1.4. Сочленение цилиндрического типа 4-го класса. Подобное сочленение может быть представлено как совокупность двух сочленений вращательного и поступательного типа 5-го класса с промежуточным звеном нулевой длины. Поэтому при описании данного сочленения с номером 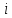 звеньев звеньев 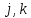 в качестве конструктивных параметров выбираем триаду углов в качестве конструктивных параметров выбираем триаду углов 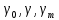 , описывающих вращательную часть сочленения, и отклонения , описывающих вращательную часть сочленения, и отклонения 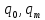 , отражающие поступательное движение. Таким образом, формализованное описание для сочленения цилиндрического типа имеет вид , отражающие поступательное движение. Таким образом, формализованное описание для сочленения цилиндрического типа имеет вид 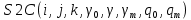 . .1.5 Сочленение типа шарнира Гука. Данная кинематическая пара является двухподвижной и может быть описана путем представления ее как совокупности двух сочленений вращательного типа 5-го класса с промежуточным звеном нулевой длины. Это звено-крестовина может рассматриваться как жесткое сочленение с осью, перпендикулярной осям вращения шарнира. При описании сочленения типа шарнир Гука в качестве конструктивных параметров выбираем триаду углов 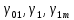 , подобную той, что была в п. 1.2, для сочленения первого звена с крестовиной; угол β между осями крестовины шарнира; триаду углов , подобную той, что была в п. 1.2, для сочленения первого звена с крестовиной; угол β между осями крестовины шарнира; триаду углов 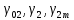 , характеризующую переход от крестовины ко второму звену сочленения. Описание шарнира Гука: , характеризующую переход от крестовины ко второму звену сочленения. Описание шарнира Гука: 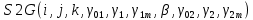 . .1.6. Сочленение сферического типа 3-го класса. Относительное движение звеньев соединенных сферическим сочленением возможно вокруг трех произвольных осей, проходящих через центр сферы, и число степеней свободы равно трем. Формализованное описание указанного сочленения  ). ).2. Звенья. Идентификаторы всех типов звеньев начинаются с символа 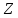 (звено) и имеют структуру вида (звено) и имеют структуру вида 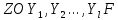 . При этом вместо . При этом вместо 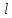 символов в идентификатор вводятся символы тех сочленений, в которые входит данное звено. Символ символов в идентификатор вводятся символы тех сочленений, в которые входит данное звено. Символ 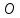 используется лишь в тех случаях, когда оно является основанием, а символ на позиции используется лишь в тех случаях, когда оно является основанием, а символ на позиции  – лишь тогда, когда оно является конечным звеном кинематической цепи манипулятора. – лишь тогда, когда оно является конечным звеном кинематической цепи манипулятора.2.1. Звенья-основания манипуляторов. В кинематических цепях манипуляторов чаще всего это звенья-однополюсники с идентификаторами типа 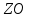 Y, где Y, где  . Однако известны и такие конструкции манипуляторов, в которых с основанием непосредственно сочленяются два и большее число звеньев. Это имеет место, например, при установке на основании манипулятора пантографического механизма. Формализованное описание основания: . Однако известны и такие конструкции манипуляторов, в которых с основанием непосредственно сочленяются два и большее число звеньев. Это имеет место, например, при установке на основании манипулятора пантографического механизма. Формализованное описание основания: 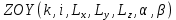 . .2.2. Подвижные звенья. Они характеризуются, прежде всего, типом сочленений, в которые входят, а также числом связанных с ними характеристических точек манипулятора (числом символов, стоящих в их идентификаторах после 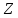 ). Для подвижных звеньев конструктивные параметры – это совокупность, данных, необходимых для однозначного определения переходов между трехгранниками осей, жестко связанными с этим звеньями в их характеристических точках. Указанные параметры для подвижных звеньев могут быть выбраны вне зависимости от типов элементов КЦМ, определяющих их характеристические точки, и последовательности их отражения в идентификаторах этих звеньев. ). Для подвижных звеньев конструктивные параметры – это совокупность, данных, необходимых для однозначного определения переходов между трехгранниками осей, жестко связанными с этим звеньями в их характеристических точках. Указанные параметры для подвижных звеньев могут быть выбраны вне зависимости от типов элементов КЦМ, определяющих их характеристические точки, и последовательности их отражения в идентификаторах этих звеньев.Описание звена, соединяющего два сочленения имеет вид  , где символ , где символ  определяется типом характеристической точки ( определяется типом характеристической точки ( ). ).2. Определение положения характеристических точек разомкнутых кинематических цепей механизмовДля определения положения и ориентации схвата манипулятора, используются только операции поворота и сдвига, т.е. те однородные преобразования, которые задаются матрицей следующего вида:  где, 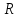 – матрица поворота – матрица поворота  ; ; 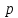 – вектор переноса – вектор переноса 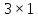 . . Пусть заданы абсолютная 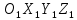 и подвижная и подвижная 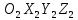 системы координат (рис.1). Будем считать, что системы координат (рис.1). Будем считать, что 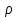 – однородный вектор в системе – однородный вектор в системе 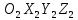 , задающий точку , задающий точку 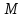 , а однородный вектор , а однородный вектор 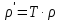 – задает точку – задает точку 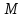 в абсолютной системе координат. Матрица в абсолютной системе координат. Матрица 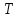 является матрицей перехода от системы координат является матрицей перехода от системы координат 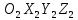 к к 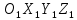 . . 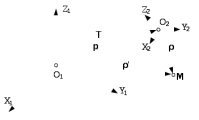 Рисунок 1 – Связь неподвижной 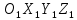 и подвижной и подвижной 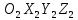 систем координат систем координатРассматривая сложные однородные преобразования, где 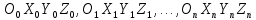 произвольно расположенные системы координат. Тогда матрица перехода от произвольно расположенные системы координат. Тогда матрица перехода от 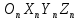 к к 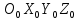 имеет следующий вид: имеет следующий вид: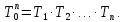 В общем случае матрица перехода от -й системы координат к 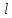 -й -й 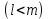 имеет следующий вид: имеет следующий вид: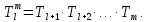 3. Алгоритм автоматизированного формирования моделей кинематики по заданному формализованному описаниюАлгоритм разработан как для формирования уравнений кинематики по исходным данным в виде формализовано описанных элементов, так и для определения положения любой характеристической точки (центра сочленения или рабочего органа) кинематической цепи относительно абсолютной системы координат. Параметры, используемые при описании элементов кинематических цепей, являются позиционными. В связи с этим, каждый элемент кинематической цепи имеет индивидуальный набор конструктивных параметров, по которым формируется однородная матрица размерностью 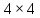 , определяющая переход между ортогональными трехгранниками осей, связанными с характеристическими точками. , определяющая переход между ортогональными трехгранниками осей, связанными с характеристическими точками.Получаемые модели кинематики являются результатом перемножения однородных матриц от каждого формализованного описанного элемента кинематической цепи. Для каждого элемента формируется одна или несколько элементарных матриц, к которым относятся три матрицы поворота: 1. матрица, описывающая поворот вокруг оси 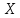 на произвольный угол на произвольный угол 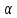 : :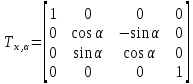 ; ;2. матрица, описывающая поворот вокруг оси 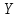 на произвольный угол на произвольный угол 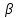 : :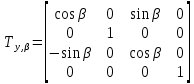 ; ;3. матрица, описывающая поворот вокруг оси 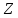 на произвольный угол на произвольный угол 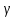 : :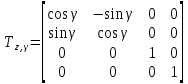 . .Параллельный перенос системы координат между двумя характеристическими точками может быть выполнен с использованием однородной матрицы переноса: 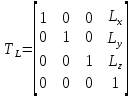 , ,где 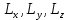 – переносы по осям координат – переносы по осям координат 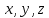 соответственно. соответственно. Для определения последовательности перемножения однородных матриц построим кинематический граф для -степенного манипулятора (рис.2). Маршрутом в полученном неориентированном графе будет конечная последовательность ребер:  такая, что каждые два соседних ребра 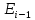 и и 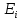 имеют общую концевую точку. Таким образом, можно написать: имеют общую концевую точку. Таким образом, можно написать: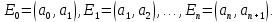 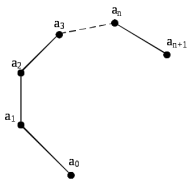 Рисунок 2 – Кинематический граф -степенного манипулятора Вершина 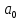 представленного графа называется начальной вершиной маршрута представленного графа называется начальной вершиной маршрута 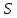 , , 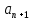 – конечной вершиной (схват манипулятора), и – конечной вершиной (схват манипулятора), и 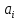 , принадлежащая двум соседним ребрам , принадлежащая двум соседним ребрам 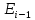 и и 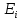 , называется внутренней, или промежуточной вершиной [6]. , называется внутренней, или промежуточной вершиной [6].Для определения положения и ориентации схвата манипулятора необходимо в маршруте кинематического графа манипулятора вычислять результирующую матрицу. Маршрут кинематического графа имеет как начальную вершину 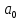 (базовая система координат), так и конечную вершину (базовая система координат), так и конечную вершину  (схват манипулятора), и может быть записан в виде: (схват манипулятора), и может быть записан в виде: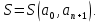 Результирующая матрица будет составлена из матриц однородных преобразований вершин и ребер кинематического графа: 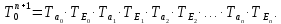 Можно также определять положения и ориентации отдельных звеньев манипулятора относительно других звеньев принятых за абсолютную систему координат. Подграф исходного графа представлен на рисунке 3.  Рисунок 3 – Подграф кинематического графа Подмаршрут для двух вершин маршрута 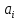 и и 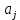 , которые являются сочленениями, в этом случае будет иметь следующий вид: , которые являются сочленениями, в этом случае будет иметь следующий вид: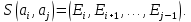 Результирующая матрица будет вычисляться следующим образом: 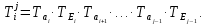 Таким образом, в рамках данного метода необходимо записывать маршрут или подмаршрут кинематического графа, начальной вершиной которого является характеристическая точка абсолютной системы координат, а концом характеристическая точка подвижного звена или рабочего органа, положение и ориентацию которого необходимо определить. 4. Описание разработанного программного обеспеченияПрограммное обеспечение реализовано на языке Object Pascal в среде объектно-ориентированного программирования Delphi 7.0. В основе разработки приложения в среде Delphi лежит проект. Центральной частью проекта является форма, на которую помещаются необходимые для решения конкретной задачи компоненты. В такой последовательности: проект – форма – компоненты, и выполнено программное обеспечение, реализующее поставленную задачу, что делает его интерфейс предельно понятным и удобным для использования. Главная форма разработанного программного обеспечения представлена на рисунке 4. Условно интерфейс программы можно разделить на четыре составляющие. 1. Ввод информации. Программное обеспечение в первую очередь должно решать задачу автоматизированного формирования математических моделей кинематики исходя из заданного формализованного описания кинематической цепи разомкнутого механизма. Здесь возникает проблема правильной записи всей совокупности данных описывающих каждый элемент кинематической цепи для их последующего использования. С этой целью в программе предусмотрен удобный ввод структурных и параметрических данных, а также выбор идентификатора. Как показано на рисунке 3, выбор произвольного идентификатора реализован с использованием выпадающего списка выбора – компонента «ComboBox», который представляет собой комбинацию компонентов «Edit» и «ListBox». Каждому идентификатору соответствует индивидуальный набор параметров, ввод которых осуществляется компонентом «StringGrid», который обладает мощными возможностями для представления текстовой информации в табличном виде. Использование данного компонента является наиболее удобным, т.к. количество его столбцов зависит от выбранного идентификатора, что исключает последующих ошибок при вводе заданных параметров. Преимущество использования выпадающего списка выбора для ввода идентификаторов в сравнении с простыми текстовыми полями также связано с выводом информации о каждом конкретном идентификаторе, что в значительной степени облегчает пользователю работу при формализованном описании кинематических цепей. Для удобства данный раздел также разделен на три части для ввода элементов разного типа: звенья-основания, сочленения и подвижные звенья.  Рисунок 4 – Интерфейс разработанного программного обеспечения Рисунок 4 – Интерфейс разработанного программного обеспечения2. Отображение вводимой информации. Вводимое формализованное описание выводится в текстовый компонент «Memo», который в общем случае используется для ввода пользователем и отображения многострочного текста без функций форматирования. Для удобства пользования в программе также предусмотрена функция загрузки уже имеющегося формализованного описания с помощью команды Меню – Файл – Открыть…, а также сохранение набранного посредством команды Меню – Файл – Сохранить ФО как… (рис.5). Последняя команда позволяет формировать банки данных об известных, и формализовано описанных конструкциях манипуляторов.  Рисунок 5 – Дополнительные функции программы 3. Установление необходимых параметров, расчет. Для того, чтобы получить модели кинематики формализовано описанной кинематической цепи необходимо установить независимый переключатель «Получить уравнения» – компонент «CheckBox» в состояние true, т.к. в случае его противоположного состояния конечным результатом будут численные значения, определяющие положение последней характеристической точки механизма. В программе также предусмотрены возможности получения моделей кинематики с учетом средних положений сочленений, будь то угол поворота до среднего положения, либо изменение длины оси одного из звеньев кинематической пары, приводящее поступательное или цилиндрическое сочленение в среднее положение. Данный переключатель необходим для учета специфики преобразования энергии в приводах кинематических пар, т.к. механизмы, содержащие пневматические и/или гидравлические кинематические пары в большинстве случаев не предусматривают отклонений до средних положений, в отличии от электроприводов. Третий независимый переключатель «Зафиксировать сочленения» позволяет фиксировать произвольные кинематические пары в кинематической цепи, что позволяет в значительной степени упростить и сократить конечную математическую модель путем исключения из уравнения переменных, соответствующих зафиксированным сочленениям. 4. Вывод результата. В ходе расчета искомых моделей кинематики в программе выполняется сортировка введенного формализованного описания, которая выводится в поле «Отсортированное ФО». Затем для каждого элемента кинематической цепи формируется однородная матрица, все матрицы выводятся в разделе «Матрицы для каждого элемента цепи». Модели кинематики выводятся в поле «Результаты вычислений» и выглядят следующим образом: X = - 5·sin(y1) - 20·sin(y1) - sin(y1)·q3; Y = 5·cos(y1) + 20·cos(y1) + cos(y1)·q3; Z = q2 + 20; где y1 - угол поворота 10-го сочленения; q2 - линейное перемещение 20-го сочленения; q3 - линейное перемещение 30-го сочленения; y4 - угол поворота 40-го сочленения. Представленные уравнения соответствуют положению схвата манипулятора МП-11. В случае состояния переключателя «Получить уравнения» false, результатом будет однородная матрица с числовыми коэффициентами. Результат программы можно сохранить в текстовом документе формата .txt с помощью команды Меню – Файл – Сохранить результат как… (рис.5). Следует так же отметить что разработанное программное обеспечение выполняет формирование математических моделей кинематики только для кинематических цепей, содержащих кинематические пары пятого класса, вращательного и поступательного типа. Не полный листинг программного кода программы (5 первых, 5 последних страниц) представлен в приложении А. ЗаключениеВ ходе выполнения научно-исследовательской работы был разработан алгоритм и программное обеспечение, позволяющее формировать математическую модель кинематики для произвольного разомкнутого механизма. Программа функционирует на основе введенного или загруженного формализованного описания и помимо своего основного назначения позволяет формировать банки данных об известных механизмах. Многофункциональность разработанного программного обеспечения позволяет получить модели кинематики практически для любого механизма с разомкнутой кинематической цепью. В качестве дальнейшего развития данной проблемы программа, решающая задачи формирования моделей кинематики для открытых кинематических цепей, может быть адаптирована для решения указанных задач в манипуляторах с параллельной кинематикой, таких как трипод, гексапод, и т.д. Такие манипуляторы имеют более высокий показатель грузоподъемности, высокую точность позиционирования рабочего органа и относительно высокую жесткость. Также дальнейшая работа над данной темой может быть связана с использованием подобного подхода для формализованного описания и формирования кинематических моделей мобильных роботов, а в дальнейшем и для решения обратных задач кинематики мобильных роботов. Решение задач данного класса в свою очередь необходимо для автоматического управления роботами данного класса в условиях изменения их кинематической структуры. Практической реализаций поставленной задачи может стать создание специализированного программного обеспечения для встраиваемых компьютерных систем мобильных роботов. Список литературы:1. Малышенко А.М. Формализованное описание структур и параметров кинематических цепей манипуляторов// Известия АН СССР. Машиноведение № 4, 1989 г.; 2. Зенкевич С.Л., Ющенко А.С. Управление роботами. Основы управления манипуляционными роботами: Учеб. для вузов – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 400 с.; 3. Фу К., Гонсалес Р. Робототехника: Пер. с англ. – М.: Мир, 1989. – 624 с.; 4. Артоболевский И.И. Теория механизмов и машин: учеб. для втузов. – 4-е изд., перераб. и доп. – М.: Наука, 1988. – 640 с.; 5. Пестриков В.М., Маслобоев А.Н. Delphi на примерах. – СПб.: БХВ-Петербург, 2005. – 496 с. 6. Оре О., Теория графов: Пер. с англ. / Под ред. Воробьева Н.Н. 2-е изд. – М.: Книжный дом «ЛИБРОКОМ», 2009. – 352 с. |
