Бу. Научноисследовательская работа по дисциплине Механика деформируемого твёрдого тела
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
2.5. Экстремальные свойства предельных состояний деформирования Две теоремы, приведенные в этом разделе, позволяют получить нижнюю и верхнюю оценки для предельного значения параметра нагружения (Ю.Н. Работнов [3], Н. Н. Малинин [10], И. Г. Терегулов [11]). Эти теоремы были впервые сформулированы и доказаны А.А. Гвоздевым в малодоступной публикации в 1934 г.; они многократно переоткрывались, независимо, разными авторами. Распределение напряжений Пусть Вычитая (20) из (19), получим: Из постулата Друккера следует, что левая часть уравнения (21) неотрицательна, поэтому неотрицательна и правая часть: 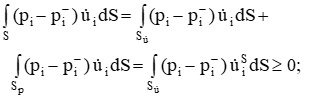 Здесь учтено, что на Итак, мощность действительных поверхностных сил на заданных скоростях больше мощности, развиваемой поверхностными силами, соответствующими любой другой статически возможной системе напряжений. Это утверждение составляет содержание так называемой статической теоремы о предельном состоянии. Неравенство (22) служит для нижней оценки несущей способности тела. Если внешняя нагрузка сводится к одной обобщенной силе Q, которой соответствует обобщенная скорость перемещения в этом случае в неравенстве (22) скорость 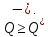 (23) (23)Если нагрузки заданы в виде Здесь 0 – опасное значение параметра . Рассмотрим суть так называемой кинематической теоремы о предельном состоянии. Пусть Прибавим и вычтем в правой части этого равенства интеграл от Согласно постулату Друккера второй член в правой части этого равенства неотрицателен, поэтому Если внешняя нагрузка представляется одной обобщенной силой Q , то  (26) (26)Правая часть этого неравенства известна, если задано кинематически возможное поле скоростей Неравенство (25) служит для верхней оценки несущей способности. Из (26) следует, что действительная предельная нагрузка не больше кинематически возможной нагрузки. (Кинематически возможной называют нагрузку, при действии которой конструкция превращается в механизм при соблюдении наложенных на нее кинематических связей). 2.6. Кинематический и статический методы определения несущей способности конструкций. Сведение задачи к задаче линейного программирования Применяя оценки (23) и (26), можно получить интервал, в котором заключено истинное значение предельной нагрузки Q. Если верхняя и нижняя оценки совпадают, то получено точное решение задачи о несущей способности (доказательство соответствующей теоремы о единственности решения можно найти, например, в книге [3] Ю.Н. Работнова). Нахождение кинематически возможных полей скоростей, которые не обязательно должны быть непрерывными, не встречает больших трудностей; варьируя эти поля, находят нижнюю грань Построение статически допустимых полей встречает бóльшие трудности, связанные главным образом с тем, что определенные в пластических областях поля напряжений должны допускать продолжения в жесткие зоны, притом такое, что условие пластичности нигде не превышается. Варьируя поле допустимых напряжений Параметр внешней нагрузки Статический и кинематический методы решения задач о несущей способности конструкций основаны на двух теоремах, суть которых изложена в предыдущем разделе. Для сужения "вилки" часто используют методы математического, в частности, линейного, программирования. Общая задача линейного программирования заключается в следующем (Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. [12]) . Дана линейная целевая функция и система линейных ограничений  (29) (29)где n > m; Планом, или допустимым решением, задачи линейного программирования называют вектор Оптимальным планом, или оптимальным решением, задачи линейного программирования называют план, доставляющий наименьшее значение целевой функции (28). В статическом методе решения задачи о несущей способности тела используют уравнения равновесия (10), (11) и уравнение предельной поверхности (14). Если В кинематическом методе используют уравнение баланса мощностей (18), кинематические граничные условия (12), уравнение предельной поверхности (14), соотношения ассоциированного закона деформирования (13) и соотношения (15). Используя (18) определяют выражение для Дискретизацию объекта расчета осуществляют, в большинстве случаев, с использованием метода конечных разностей, или метода конечных элементов. Обзор литературы по теории предельного равновесия приведён, в частности, в работах Сибгатуллина Э. С. [13], [14] и Сибгатуллина К. Э. [15]. 3. Пример решения задачи 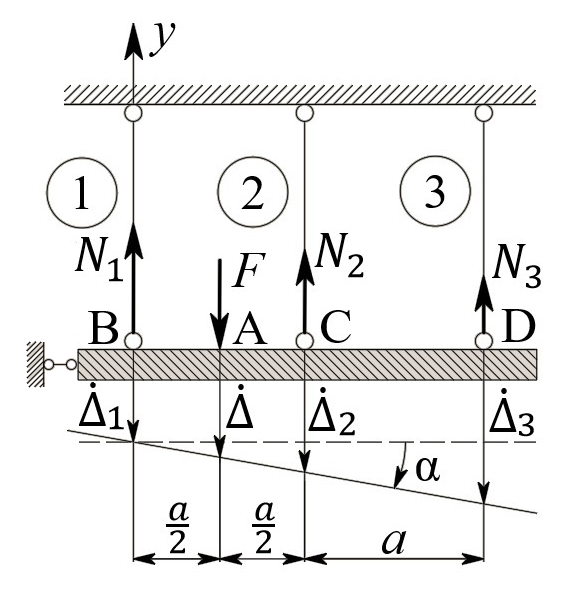 Рис. 4. Бесконечно жесткий брус подвешен на трех вертикальных стержнях (рис. 4). Известны длины стержней 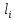 , площади поперечных сечений стержней , площади поперечных сечений стержней 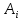 , пределы текучести материалов стержней , пределы текучести материалов стержней 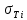 (i= (i=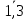 ). Определить предельную нагрузку ). Определить предельную нагрузку 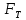 для рассматриваемой стержневой системы при для рассматриваемой стержневой системы при 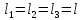 , , 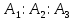 = 1:1/2:1/12, = 1:1/2:1/12, 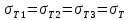 . .3.1. Решение задачи кинематическим методом Согласно этому методу, истинному механизму разрушения соответствует минимальное значение кинематически возможной нагрузки 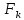 . Для рассматриваемой системы возможны всего три различных механизма разрушения. Поэтому истинный механизм разрушения с min . Для рассматриваемой системы возможны всего три различных механизма разрушения. Поэтому истинный механизм разрушения с min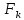 можно установить путем перебора этих кинематически возможных механизмов разрушения. можно установить путем перебора этих кинематически возможных механизмов разрушения.Согласно принципу возможных перемещений имеем: 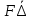 = =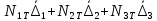 . (31) . (31)Здесь 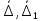 , ,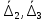 – скорости кинематически возможных перемещений точек А, В, С, D, соответственно (рис. 2), – скорости кинематически возможных перемещений точек А, В, С, D, соответственно (рис. 2), 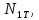 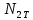 , , 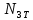 – усилия растяжения-сжатия стержней 1, 2, 3, соответственно, в состоянии разрушения системы: – усилия растяжения-сжатия стержней 1, 2, 3, соответственно, в состоянии разрушения системы: 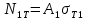 , , 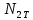 = = 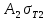 , , 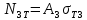 . .Условия совместности скоростей перемещений: 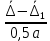 = = 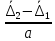 = = 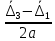 = = 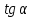 . (32) . (32)Так как в кинематическом методе важно только направление вектора скоростей деформации, можно принять следующее дополнительное условие: 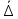 =1. (33) =1. (33)С учетом исходных соотношений между 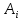 , , 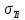 и условия (33), уравнение (31) можно записать в следующем виде: и условия (33), уравнение (31) можно записать в следующем виде: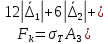 | |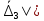 ). (34) ). (34)1. Пусть 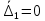 ; тогда, согласно (32) и (33), имеем ; тогда, согласно (32) и (33), имеем 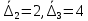 . Согласно (34) получаем: . Согласно (34) получаем: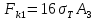 . (35) . (35)2. Пусть 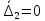 ; тогда ; тогда 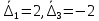 . .Так как скорость диссипации механической энергии не может быть отрицательной величиной, т.е. 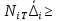 0 всегда, в (34) 0 всегда, в (34) 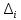 необходимо подставлять по модулю. С учетом этого имеем: необходимо подставлять по модулю. С учетом этого имеем: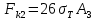 . (36) . (36)3. Пусть теперь 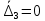 ; тогда, ; тогда, 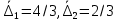 . Имеем: . Имеем: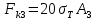 . (37) . (37)Из кинематически возможных нагрузок (35, 36, 37) выбираем наименьшее значение: 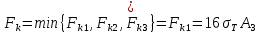 . (38) . (38)Значение (38) оценивает действительную разрушающую нагрузку 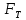 сверху: сверху: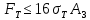 . (39) . (39) |
