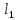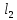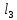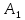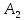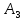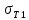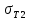Бу. Научноисследовательская работа по дисциплине Механика деформируемого твёрдого тела
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГАОУ ВО «КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» НАБЕРЕЖНОЧЕЛНИНСКИЙ ИНСТИТУТ (ФИЛИАЛ) Исследование несущей способности шарнирно-стержневой системы Научно-исследовательская работа по дисциплине «Механика деформируемого твёрдого тела» Учебно-методическое пособие для аспирантов направления подготовки 01.06.01. Математика и механика. Направленность (профиль) подготовки 01.02.04. Механика деформируемого твёрдого тела; для магистрантов, обучающихся по направлению подготовки 08.04.01. Строительство Набережные Челны 2020 Исследование несущей способности шарнирно-стержневой системы. Научно-исследовательская работа по дисциплине «Механика деформируемого твёрдого тела». Учебно-методическое пособие для аспирантов направления подготовки 01.06.01. Математика и механика. Направленность (профиль) подготовки 01.02.04. Механика деформируемого твёрдого тела; для магистрантов, обучающихся по направлению подготовки 08.04.01. Строительство / Э. С. Сибгатуллин, К. Э. Сибгатуллин, М. Э. Сибгатуллин –Набережные Челны: НЧИ КФУ, 2020, 36 с. Учебно-методическое пособие по выполнению научно-исследовательской работы разработано в соответствии с требованиями ФГОС высшего образования к уровню подготовки выпускника по направлению подготовки 01.06.01 «Математика и механика», 08.04.01 «Строительство». Излагаются теоретический материал, пример расчёта и задание для самостоятельной работы. Рецензенты: д-р физ.-матем. наук, профессор Н. С. Габбасов, ФГАОУ ВО «Казанский федеральный государственный университет» канд. техн. наук, доцент К. Ф. Исламов, ФГАОУ ВО «Казанский федеральный государственный университет» Печатается в соответствии с решением научно-методического совета Набережночелнинского института КФУ. © Набережночелнинский институт КФУ, 2020 год 1. Задание для самостоятельной НИР студента (аспиранта) Бесконечно жесткий брус шарнирно подвешен на трех вертикальных стержнях (рис. 1). Определить предельную несущую способность системы. Исходные данные задачи взять из таблицы 1, согласно индивидуальному шифру студента. Индивидуальный шифр студента (аспиранта) совпадает с последними четырьмя цифрами номера его зачетной книжки либо может быть назначен преподавателем. Под этими цифрами нужно написать буквы А, Б, В, Г. Буква и соответствующая цифра определяют координаты личных исходных данных в табл. 1. Например, для шифра 9156 исходные данные в табл. 1 выделены. В табл. 1 расстояния и длины стержней даны в метрах, площади поперечных сечений стержней 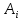 – в – в 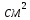 , пределы текучести материалов стержней , пределы текучести материалов стержней 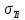 – в ГПа (i=1, 2, 3). Задачу необходимо решить с использованием кинематического и статического методов теории предельного равновесия (см. пример решения). Рассмотреть шесть вариантов задачи, варьируя между собой заданные площади поперечных сечений стержней. Результаты расчетов оформить в виде следующей таблицы 2 (например, для шифра 9156): – в ГПа (i=1, 2, 3). Задачу необходимо решить с использованием кинематического и статического методов теории предельного равновесия (см. пример решения). Рассмотреть шесть вариантов задачи, варьируя между собой заданные площади поперечных сечений стержней. Результаты расчетов оформить в виде следующей таблицы 2 (например, для шифра 9156):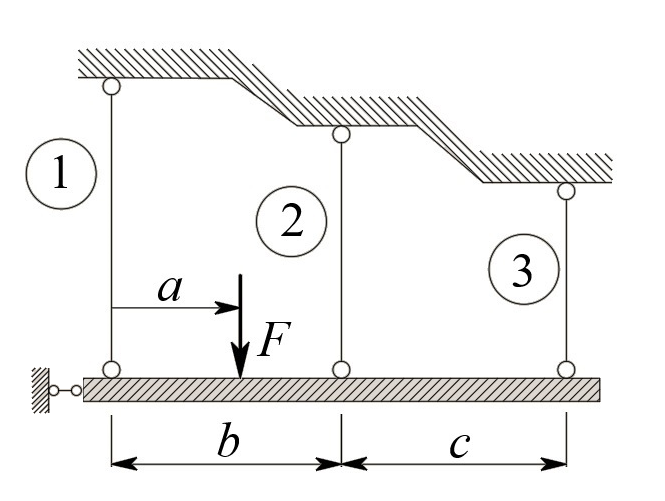 Рис. 1. Таблица 1
Таблица 2
В табл. 2 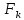 , , 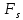 – верхняя и нижняя оценки предельной нагрузки, соответственно, V= – верхняя и нижняя оценки предельной нагрузки, соответственно, V= 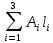 – суммарный объем несущих стержней. – суммарный объем несущих стержней.2. Основные положения теории предельного равновесия. Методы решения задач о несущей способности элементов конструкций 2.1. Поверхность нагружения Для математической постановки задачи механики сплошной среды необходимы соотношения, определяющие связь между силовыми и кинематическими параметрами в элементе среды. Разрушение материала (пластическое, или хрупкое) является, как правило, необратимым процессом. Когда деформирование среды является необратимым процессом, поведение материала, предписываемое законом деформирования, должно зависеть от направления процесса. Такая своеобразная неаналитичность приводит к появлению в фазовом пространстве внутренних параметров некоторых предельных поверхностей, очертание и изменение которых оказывает решающие влияние на форму самого закона деформирования (В. Д. Клюшников [1]). В результате изменения внешних сил, действующих на тело, и перемещений его границы, происходит изменение напряженно-деформированного состояния каждого его элемента. Процесс изменения напряжений Любой из этих процессов можно представить в виде кривых – траекторий в некоторых фазовых пространствах, координатами которых являются параметры либо напряженного, либо деформированного, состояний. В пространстве напряжений каждому напряженному состоянию Аналогичным образом определяют пространство деформаций. Иногда одно и то же девятимерное декартово пространство используют как для представления напряжений, так и для представления деформаций, откладывая вдоль данного орта пространства одноиндексные компоненты тензоров (например, Мы ограничимся рассмотрением только таких материалов, для которых результат деформирования не зависит от скорости процесса нагружения в данное напряженное состояние (упруго-пластические материалы). Обобщение свойств деформирования упругопластического тела, которые оно проявляет при одноосном растяжении–сжатии, на случай сложного напряженного состояния приводит к концепции о существовании поверхности нагружения (В. Д. Клюшников [1]), которая состоит в следующем (рис. 2). 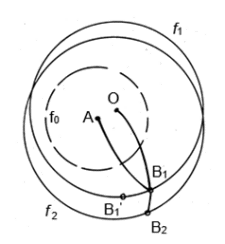 Рис. 2 Для каждой текущей точки Если же траектория выходит наружу поверхности нагружения, построенной для предыдущей точки, например, траектория Процесс, при котором возникают необратимые деформации, называют активным нагружением, а процесс, сопровождающейся только упругим деформированием – пассивным нагружением, или – разгрузкой. Процесс, при котором траектория нагружения, начиная с некоторой точки, идет вдоль поверхности нагружения, построенной для этой точки, например B1B1', является пограничным между активным и пассивным, и его называют нейтральным нагружением. Свойства деформирования при нейтральном нагружении определяют как предельные. Деформацию элемента материала ij часто представляют как сумму упругой (обратимой) Форма и размеры поверхности нагружения определяются только пластической частью деформации и историей ее изменения. Следовательно, аналитически уравнение текущей предельной поверхности можно представить в виде где через np условно представлены параметры, зависящие от истории изменения Следует отметить, что представление общей деформации в виде двух аддитивных составляющих является всего-навсего широко распространенной гипотезой. При случайной или методологической ошибках в выделении пластической составляющей из общей деформации могут возникнуть существенные искажения экспериментального результата (А. Н. Супрун [2]). 2.2. Принцип максимума Мизеса и постулат Друккера. Ассоциированный закон деформирования Принцип максимума Р. Мизеса формулируется следующим образом (Ю. Н. Работнов [3]). Пусть задано распределение скоростей Здесь Утверждается, что для истинного напряженного состояния мощность диссипации не меньше, чем для любого допустимого состояния Это условие записывают следующим образом: Д. Друккером было высказано следующее утверждение: новая необратимая деформация в упруго–пластических телах не может возникнуть самопроизвольно; для ее создания нужно затратить энергию. В дальнейшем это положение было развито в его многочисленных работах (см., например, Д. Друккер [4]), и был назван постулатом устойчивости материала. Согласно мнению самого Д. Друккера [4], постулат устойчивости материала является не законом природы, а средством, позволяющим дать общую классификацию материалов, которая выходит за пределы понятий, охватывающих специальные категории: упругость, пластичность, вязкость и т.д. Для материалов с независящими от времени свойствами критерий устойчивости в малом для произвольного ненулевого нагружения имеет следующий вид: Критерий устойчивости в малом для произвольного цикла нагрузки и разгрузки имеет вид: В теории пластичности доказывают (например, В. Д. Клюшников [1]),что если условие (7) выполняется, то поверхность нагружения является выпуклой, а вектор 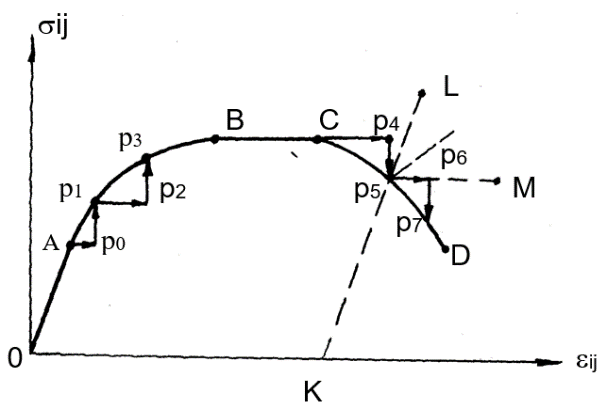 Рис. 3 Предполагая справедливым концепцию поверхности нагружения и неравенство (7) можно заключить, что в регулярной точке поверхности нагружения  (8) (8)Здесь  (9) (9)Здесь отличны от нуля только те , для которых выполняются условия, указанные в (9). Как справедливо отмечено в книге [1] В. Д. Клюшникова, независимость действия пластических механизмов – явление, не свойственное нелинейной механике. Однако соотношения (9) нашли довольно широкое применение в теории пластичности. Это объясняется их относительной простотой. Формулы (8), (9) являются соотношениями теории пластического течения и они позволяют решать геометрически и физически нелинейные задачи теории пластичности, двигаясь малыми шагами вдоль диаграммы ij – ij. Соотношения в (8), (9), связывающие Следует отметить, что в принципе возможны соотношения пластичности, не удовлетворяющие условию градиентальности, но случай этот нужно отнести к разряду необычных и считать оправданным только тогда, когда явным образом обнаруживается структурная неустойчивость материала (В. Д. Клюшников [1]). 2.3. Постановка задачи о предельном равновесии тел Общая постановка задачи об оценке несущей способности элемента конструкции состоит в следующем (Ю. Н. Работнов [3], М. И. Ерхов [5]). На части поверхности Для решения поставленной задачи привлекаются следующие соотношения: Уравнения равновесия Граничные условия для напряжений Кинематические граничные условия Соотношения ассоциированного закона деформирования  (13) (13)Уравнение поверхности нагружения, соответствующие предельному состоянию (уравнение поверхности текучести или поверхности прочности) Поля скоростей перемещений и скоростей деформаций могут иметь допустимые разрывы и связаны между собой соотношениями Решение полной системы уравнений (10) – (15) в общем случае является чрезвычайно сложной задачей. Аналитические решения о несущей способности конструкций получены только для ограниченного круга задач. 2.4. Уравнение баланса мощностей Вариационные принципы механики являются исключительно мощным средством исследования конструкций. Хотя соответствующие системы разрешающих уравнений механики сплошной среды вытекают как условия стационарности определенных функционалов, тем не менее, вариационные формулировки имеют ряд преимуществ (К. Вашидзу [6]). В частности, вариационные принципы иногда приводят к формулам для верхней и нижней оценок точного решения задачи. Основой для вариационной формулировки задач во многих случаях служит принцип возможных перемещений (принцип виртуальной работы) (Н. Н. Бухгольц [7]), который можно сформулировать так: пусть механическая система, на которую наложены заданные геометрические связи, находится в равновесии под действием приложенных сил. Тогда сумма всех виртуальных работ 'W всех внешних и внутренних сил, действующих на эту систему, на любых бесконечно малых виртуальных перемещениях, удовлетворяющих заданным геометрическим связям, равна нулю: Здесь 'W не является вариацией некоторой функции состояния W, а всего лишь означает полную виртуальную работу. Тем не менее, из (16) следуют для многих важных, для практики, случаев, соотношения, которые имеют явно вариационный характер. Принцип виртуальной работы остается справедливым независимо от соотношений напряжения – деформации и существования потенциальных функций. Для тел, имеющих жесткие (недеформируемые) области и разрывные поля напряжений и деформаций (перемещений) уравнение (16) имеет следующий вид (М. И. Ерхов [5]): Здесь V – объем тела; Sl – l-ая поверхность разрыва виртуальных перемещений; ijnj – компоненты напряжений на Sl; l – номер поверхности разрыва виртуальных перемещений; nj – компоненты нормали к соответствующей поверхности; [ui] – величина разрыва виртуального перемещения; pi – компоненты вектора поверхностной нагрузки; Xi – компоненты вектора объемной нагрузки; Уравнения статической теории пластичности не содержат времени; однако, разделив их на dt, можно формально перейти от приращений dij к скоростям деформации Это уравнение является уравнением баланса мощностей всех сил, действующих на рассматриваемое тело. В научной литературе оно приводится под различными названиями. Например, в книге Л.М. Качанова [8] – "основное энергетическое уравнение"; в книге М.И. Ерхова [5] – "принцип виртуальной мощности"; в книге Д.Д. Ивлева [9] – " уравнение скорости виртуальных работ"; в книге Ю.Н. Работнова [3] – "уравнение равновесия в форме Лагранжа". | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||