Бу. Научноисследовательская работа по дисциплине Механика деформируемого твёрдого тела
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
3.2. Решение задачи статическим методом В этом случае используем: а) Уравнения равновесия ∑У=0, ∑ 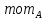 =0; (40) =0; (40)б) Условия прочности 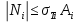 (i=1, 2, 3). (41) (i=1, 2, 3). (41)Из схемы загружения видно (рис. 4), что в данном конкретном случае 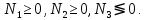 С учетом этого (40) и (41) запишем в виде: С учетом этого (40) и (41) запишем в виде: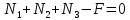 , , 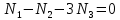 , ,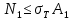 , , 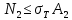 , , 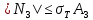 . (42) . (42)Из второго уравнения (42) находим 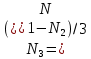 . (43) . (43)Подставим (43) в остальные соотношения из (42): F = (4/3) 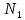 +(2/3) +(2/3)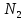 , (44) , (44)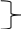 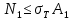 , , 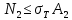 , ,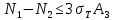 , , 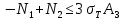 . (45) . (45)Теперь задача формулируется так: найти max F из (44) при выполнении условий (45). Это – задача линейного программирования. В данном случае она может быть решена графически (рис. 5). 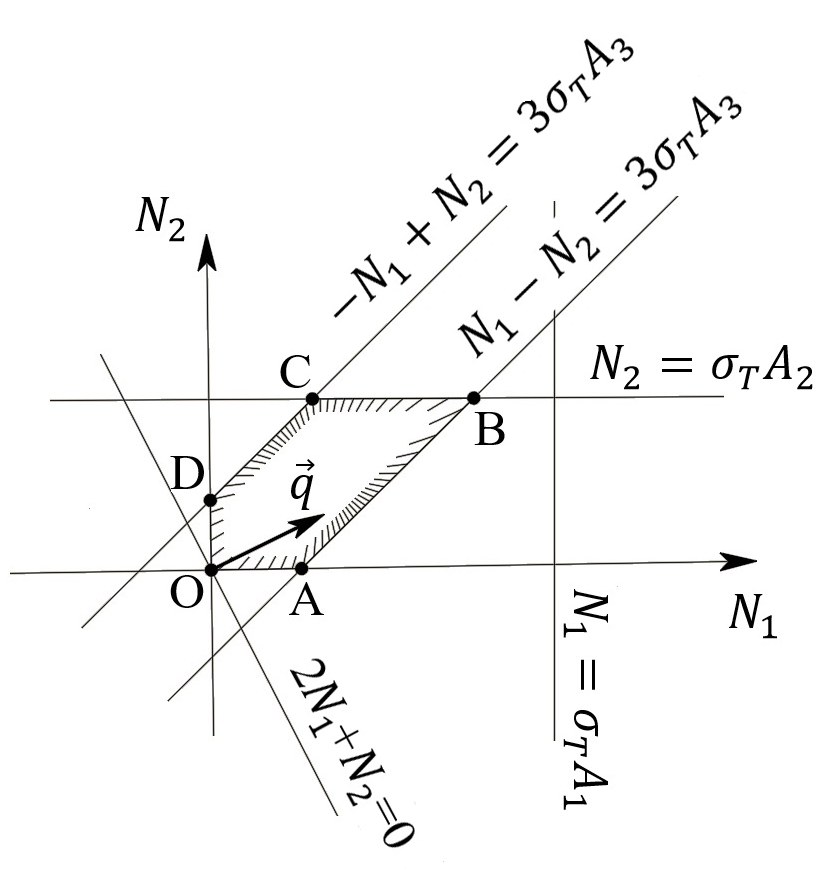 Рис. 5. Условия (45) в плоскости 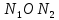 выделяют невогнутую область допустимых решений задачи, ограниченную многоугольником OABCDO. Вектор выделяют невогнутую область допустимых решений задачи, ограниченную многоугольником OABCDO. Вектор 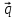 , перпендикулярный прямой (4/3) , перпендикулярный прямой (4/3)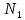 +(2/3) +(2/3)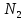 =0, показывает направление роста функции (44). Ясно, что в данном случае искомым является решение, соответствующее точке В на рис. 5. Используя координаты точки В, находим: =0, показывает направление роста функции (44). Ясно, что в данном случае искомым является решение, соответствующее точке В на рис. 5. Используя координаты точки В, находим: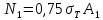 , , 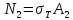 , , 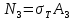 ; ;maxF= 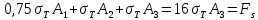 . (46) . (46)Статистический метод дает оценку снизу для действительной разрушающей нагрузки 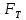 : :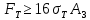 . (47) . (47)Как видно из (39) и (47), в данном случае имеем: 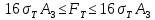 . (48) . (48)Верхняя и нижняя оценки для 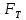 совпали. Согласно теории предельного равновесия, действительная разрушающая нагрузка в данном случае равна совпали. Согласно теории предельного равновесия, действительная разрушающая нагрузка в данном случае равна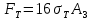 . (49) . (49)4. Требования к оформлению отчёта по НИР студента Сделать обзор научных публикаций по теории предельного равновесия за последние пять лет. Привести краткое изложение сути теоретического материала, ориентируясь на настоящую методическую работу. Решить индивидуальный вариант задачи и заполнить табл. 2, разобравшись предварительно с примером решения, приведённым в настоящей методической разработке. Привести результаты (подробные) решения индивидуального варианта задачи. Сделать выводы, где, в частности, отметить, какой из рассмотренных шести вариантов обеспечивает наибольшую несущую способность, а какой имеет наименьший суммарный объём стержней. Привести список литературы по теории предельного равновесия, где использовать, в частности, результаты пункта 1. Отчёт оформить с соблюдением требований соответствующих нормативных документов. Машинописный текст – через 1,5 интервала, с одной стороны листа. Чертежи выполнить в масштабе. Формат чертежей – А4. Объём отчёта 20÷25 страниц. Литература Клюшников В.Д. Математическая теория пластичности. – Изд-во Московского университета, 1979. – 207с. Супрун А.Н. К проблеме существования конических точек и вогнутостей на поверхности текучести металлов // МТТ. – 1991. – N4. – С.180–185. Работнов Ю. Н. Механика деформируемого твёрдого тела. – М.: Наука, 1988. – 712 с. Друккер Д. О постулате устойчивости материала в механике сплошной среды // Механика. – 1964. – N3. – С.115–128. Ерхов М.И. Теория идеально пластических тел и конструкций. – М.: Наука, 1978. – 352с. Вашидзу К. Вариационные методы в теории упругости и пластичности. Пер. с англ. — М.: Мир, 1987. — 542 с. Бухгольц Н.Н. Основной курс теоретической механики. Часть I. – М.: Наука,1972. – 468с. Качанов Л. М. Основы теории пластичности. – М.: Наука, 1969. – 420 с. Ивлев Д.Д. Теория идеальной пластичности. – М.: Наука, 1966. – 232с. Малинин Н. Н. Прикладная теория пластичности и ползучести. – М.: Машиностроение, 1968. – 400 с. Терегулов И. Г. Сопротивление материалов и основы теории упругости и пластичности. – М.: Высшая школа, 1984. – 472 с. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. – М.: Высшая школа, 1976. – 352с. Сибгатуллин Э. С. Несущая способность и оптимальное проектирование жёсткопластических оболочек вращения. – Дисс. на соиск. уч. степ. к. ф.-м. н. – Казань, 1986. – 241 с. Сибгатуллин Э. С. Математическое моделирование прочности и несущей способности анизотропных и композитных элементов конструкций – дисс. на соиск. уч. степ. д. ф.-м. н. – Набережные Челны, 2001. – 405 с. Сибгатуллин К.Э. Разработка методов расчета на прочность несущих систем грузовых автомобилей с учетом пластических деформаций. – Дисс. на соиск. уч. степ. к. т. н. – Набережные Челны, 2009. – 151 с. Отпечатано в Издательско-полиграфическом центре Набережночелнинского института Казанского (Приволжского) федерального университета Подписано в печать ____________ г. Формат 60х84/16. Печать ризографическая. Бумага офсетная. Гарнитура «TimesNewRoman». Усл. п. л. 2,7. Уч.-изд. л. 2,7. Тираж ___ экз. Заказ No _____. 423810, г. Набережные Челны, Новый город, проспект Мира, 68/19тел./факс(8552) 39-65-99 e-mail: ic-nchi-kpfu@mail.ru |
